60 Of 33
interactiveleap
Sep 22, 2025 · 5 min read
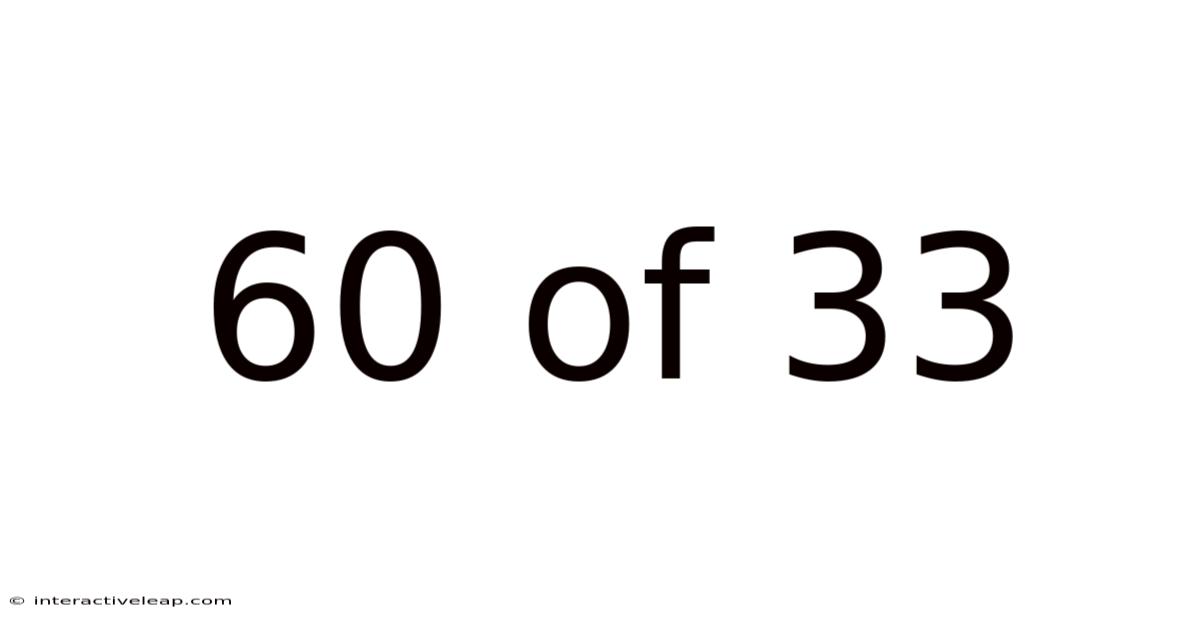
Table of Contents
Decoding the Enigma: Understanding the Fraction 60/33 and its Implications
The seemingly simple fraction 60/33 might appear insignificant at first glance. However, exploring its intricacies reveals a fascinating journey into the world of mathematics, encompassing simplification, decimal representation, percentage calculation, and real-world applications. This article aims to provide a comprehensive understanding of 60/33, going beyond a simple answer to delve into the underlying concepts and their practical significance. We will explore its simplification, convert it to a decimal, examine its percentage equivalent, and discuss potential applications in various fields.
Introduction to Fractions and Simplification
A fraction, at its core, represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The fraction 60/33 indicates that we have 60 parts out of a total of 33 parts. This immediately suggests an improper fraction – the numerator is larger than the denominator – implying a value greater than 1. Before further analysis, it’s crucial to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator and denominator.
The GCD of 60 and 33 is 3. Dividing both the numerator and the denominator by 3, we obtain the simplified fraction:
60 ÷ 3 = 20 33 ÷ 3 = 11
Therefore, the simplified form of 60/33 is 20/11. This simplified fraction is much easier to work with in subsequent calculations.
Converting 60/33 (or 20/11) to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. For the simplified fraction 20/11:
20 ÷ 11 ≈ 1.818181...
The result is a recurring decimal, meaning the digits "81" repeat infinitely. This can be represented as 1.818181... or using a bar notation: 1.$\overline{81}$. Understanding recurring decimals is important because many fractions, when converted to decimals, do not yield a finite number of digits.
Calculating the Percentage Equivalent
To express 60/33 (or 20/11) as a percentage, we multiply the decimal equivalent by 100:
1.818181... × 100 ≈ 181.8181...%
This means that 60/33 represents approximately 181.82%. The percentage representation provides a readily understandable way to compare and contrast proportions in various contexts.
Real-World Applications of Fractions Like 60/33
Understanding and manipulating fractions like 60/33 isn't confined to the abstract realm of mathematics. They have diverse applications in everyday life and various professional fields:
-
Business and Finance: Fractions are crucial for calculating ratios, proportions, and percentages in financial analysis. For example, calculating return on investment (ROI), profit margins, or debt-to-equity ratios frequently involves fractional calculations. A scenario could involve comparing the performance of two investments where one yielded 60 units of profit against an investment of 33 units.
-
Engineering and Construction: Engineers use fractions extensively in blueprints, measurements, and calculations related to scaling, proportions, and material quantities. For instance, determining the ratio of different components in a concrete mix or calculating the dimensions of a scaled model would involve fraction manipulation.
-
Cooking and Baking: Recipes frequently employ fractions to specify ingredient amounts. A recipe might call for 60 grams of flour for every 33 grams of sugar, requiring the baker to understand and work with the fraction 60/33 to maintain the correct proportions.
-
Science and Research: Scientists use fractions extensively in data analysis, experiments, and measurements. For example, calculating concentrations, ratios in chemical reactions, or probabilities in statistical analysis all necessitate the understanding and manipulation of fractions.
-
Everyday Life: Dividing resources, sharing items, or calculating parts of a whole in everyday situations frequently requires fractional understanding. Imagine sharing 60 candies amongst 33 children – the concept of 60/33 is directly applicable to fairly distribute the candies.
Further Mathematical Explorations of 60/33
Beyond basic conversion, several advanced mathematical concepts relate to the fraction 60/33:
-
Continued Fractions: The fraction 20/11 can be expressed as a continued fraction, a way of representing a number as a sequence of integers. This representation provides insights into the number's properties and approximations.
-
Modular Arithmetic: Exploring 60/33 within the context of modular arithmetic reveals patterns and relationships within number systems. This branch of mathematics deals with remainders after division.
-
Diophantine Equations: These equations involve integer solutions. Exploring whether equations involving 60/33 possess integer solutions adds another layer of mathematical analysis.
-
Complex Fractions: 60/33 can be incorporated into more complex fractions, leading to more challenging calculations and providing practice with fraction manipulation.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 60/33?
- A: The simplest form of 60/33 is 20/11.
-
Q: How do I convert 60/33 to a decimal?
- A: Divide the numerator (60) by the denominator (33). This results in a recurring decimal: 1.818181...
-
Q: What is 60/33 as a percentage?
- A: 60/33 is approximately 181.82%.
-
Q: Are there any real-world applications for this fraction?
- A: Yes, fractions like 60/33 are used in various fields, including finance, engineering, cooking, science, and everyday life, to represent proportions and ratios.
Conclusion: The Significance of Understanding Fractions
The seemingly simple fraction 60/33 offers a gateway to understanding fundamental mathematical principles. Through its simplification, decimal conversion, percentage calculation, and real-world applications, we've explored its multifaceted nature. This comprehensive analysis highlights the importance of mastering fractional arithmetic, emphasizing its relevance not only in academic settings but also in the practical aspects of numerous fields. The ability to manipulate and interpret fractions is a valuable skill applicable across various disciplines, showcasing the pervasive role of mathematics in our world. From financial calculations to engineering designs, from culinary creations to scientific research, a thorough grasp of fractions remains a cornerstone of effective problem-solving and critical thinking. The seemingly mundane fraction 60/33 ultimately demonstrates the power and versatility of mathematical concepts.
Latest Posts
Latest Posts
-
Shooting And Elephant
Sep 22, 2025
-
18 5 Of 158
Sep 22, 2025
-
Pink Buttercream Cake
Sep 22, 2025
-
Finger In Mouth
Sep 22, 2025
-
18 5 Of 194
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 33 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.