60 Of 24
interactiveleap
Sep 20, 2025 · 6 min read
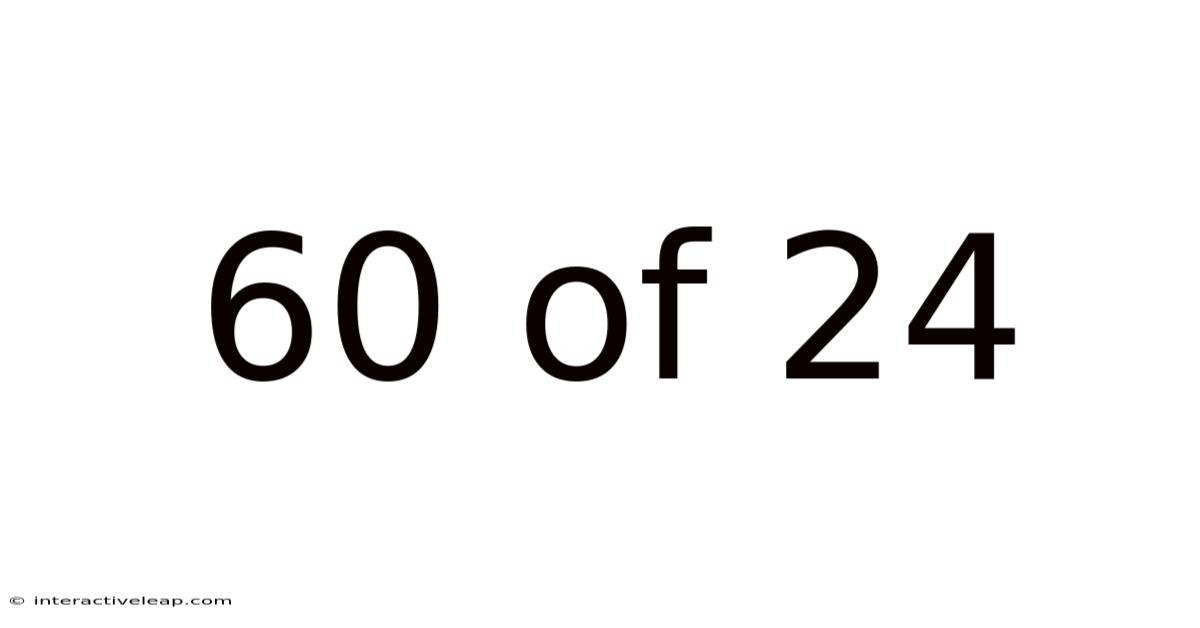
Table of Contents
Decoding the Fraction: Understanding 60/24 and its Implications
This article delves into the seemingly simple fraction 60/24, exploring its various interpretations, simplifications, and applications across different mathematical contexts. We'll move beyond a basic answer to uncover the deeper understanding of fractions, ratios, and their real-world implications. Understanding fractions like 60/24 is crucial for a strong foundation in mathematics and its applications in various fields. This comprehensive guide will equip you with the knowledge to confidently handle similar fractions and related concepts.
Introduction: The Basics of 60/24
At first glance, 60/24 appears straightforward. It represents a fraction, where 60 is the numerator (the top number) and 24 is the denominator (the bottom number). This fraction indicates a part-to-whole relationship; 60 represents a portion of a whole that's divided into 24 equal parts. However, this simple representation opens the door to several mathematical operations and interpretations.
Simplifying the Fraction: Finding the Lowest Terms
Before exploring further, it's essential to simplify the fraction to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by it. The GCD of 60 and 24 is 12. Dividing both the numerator and denominator by 12, we get:
60 ÷ 12 = 5 24 ÷ 12 = 2
Therefore, the simplified fraction is 5/2. This simplified form retains the same value as 60/24 but is more concise and easier to work with.
Representing 60/24: Different Forms
The fraction 60/24, or its simplified form 5/2, can be represented in several ways:
- Improper Fraction: 5/2 is an improper fraction because the numerator (5) is larger than the denominator (2). This signifies a value greater than one.
- Mixed Number: An improper fraction can be converted into a mixed number, which represents a whole number and a proper fraction. To do this, divide the numerator by the denominator: 5 ÷ 2 = 2 with a remainder of 1. Thus, 5/2 is equal to 2 ½.
- Decimal: Converting the fraction to a decimal involves dividing the numerator by the denominator: 5 ÷ 2 = 2.5.
Each representation – improper fraction, mixed number, and decimal – provides a different perspective on the same value. Choosing the appropriate representation depends on the context of the problem.
Understanding the Ratio: Exploring the Relationship
Beyond its fractional representation, 60/24 also signifies a ratio. It describes a relationship between two quantities – 60 and 24. This ratio can be interpreted as:
- 60 to 24: This simple ratio indicates that for every 60 units of one quantity, there are 24 units of another.
- 5 to 2: After simplification, the ratio becomes 5:2, indicating a simplified proportional relationship. This simplified ratio maintains the same proportion as the original.
The ratio concept is vital in various applications, from scaling recipes to understanding proportions in geometry and science.
Real-World Applications: Seeing 60/24 in Action
The fraction 60/24, or 5/2, appears in various real-world scenarios:
- Recipe Scaling: Imagine a recipe that calls for 24 grams of sugar and 60 grams of flour. The ratio of flour to sugar is 60/24, or 5/2. If you want to double the recipe, you would multiply both quantities by 2, maintaining the same ratio.
- Unit Conversion: Suppose you're converting units of measurement. You might encounter a scenario where 60 centimeters need to be converted to an equivalent measurement in inches (2.54 cm per inch). The conversion would involve the ratio and lead to a value expressing the equivalent in inches.
- Geometric Proportions: In geometry, the ratio of sides in similar shapes is crucial. 60/24 could represent the ratio of corresponding sides in two similar triangles.
- Data Analysis: In statistical analysis, ratios are frequently used to compare different data sets. 60/24 could represent the ratio of two different data points, offering insights into their relative magnitudes.
Mathematical Operations with 60/24:
The fraction 60/24 provides a fertile ground for practicing various mathematical operations:
- Addition and Subtraction: To add or subtract fractions, a common denominator is required. This is particularly important when dealing with mixed numbers.
- Multiplication: Multiplying fractions is straightforward: multiply the numerators and then multiply the denominators. For example, (60/24) * (1/2) = 60/48 which simplifies to 5/4 or 1 ¼.
- Division: Dividing fractions involves inverting the second fraction (the divisor) and multiplying. For example, (60/24) ÷ (1/2) = (60/24) * (2/1) = 120/24 = 5.
- Percentage Calculation: To express 60/24 as a percentage, convert it to a decimal (2.5) and then multiply by 100: 2.5 * 100 = 250%. This indicates that 60 is 250% of 24.
Further Exploration: Extending the Understanding
Beyond the immediate calculations, understanding 60/24 opens doors to more advanced mathematical concepts:
- Proportions and Ratios: The ratio 5:2 provides a foundation for understanding proportions and solving related problems involving scaling, similarity, and direct/inverse variation.
- Algebraic Equations: Fractions like 60/24 can be incorporated into algebraic equations, requiring solving for unknown variables.
- Calculus: While less directly apparent, the understanding of fractions forms a basis for concepts in calculus, such as limits and derivatives, where ratios play a crucial role.
Frequently Asked Questions (FAQ)
- Q: What is the simplest form of 60/24? A: The simplest form is 5/2.
- Q: How do I convert 60/24 to a mixed number? A: Divide 60 by 24 (which equals 2 with a remainder of 12), resulting in the mixed number 2 12/24. This further simplifies to 2 ½.
- Q: What is the decimal equivalent of 60/24? A: The decimal equivalent is 2.5.
- Q: Can I use a calculator to simplify 60/24? A: Yes, most calculators have a fraction function that will simplify fractions for you.
- Q: What are some real-world applications of understanding fractions like 60/24? A: Applications include recipe scaling, unit conversions, geometric proportions, data analysis, and numerous situations requiring proportional reasoning.
Conclusion: The Significance of Understanding Fractions
The seemingly simple fraction 60/24 reveals a wealth of mathematical concepts and practical applications. From its simplification to its representation in various forms and its role in ratios and proportions, this fraction provides a valuable learning opportunity. Mastering the manipulation and interpretation of fractions like 60/24 forms a crucial building block for more advanced mathematical studies and real-world problem-solving. The ability to work confidently with fractions is an essential skill across various disciplines and contributes significantly to a robust mathematical foundation. Remember to practice regularly and explore different problem-solving approaches to strengthen your understanding. This will not only help you understand simple fractions but also prepare you for more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
Greenmeadow Community Farm
Sep 20, 2025
-
Microlitres To Millilitres
Sep 20, 2025
-
85c To F
Sep 20, 2025
-
Compass And Protractor
Sep 20, 2025
-
12 Of 300
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.