60 Of 180
interactiveleap
Sep 13, 2025 · 6 min read
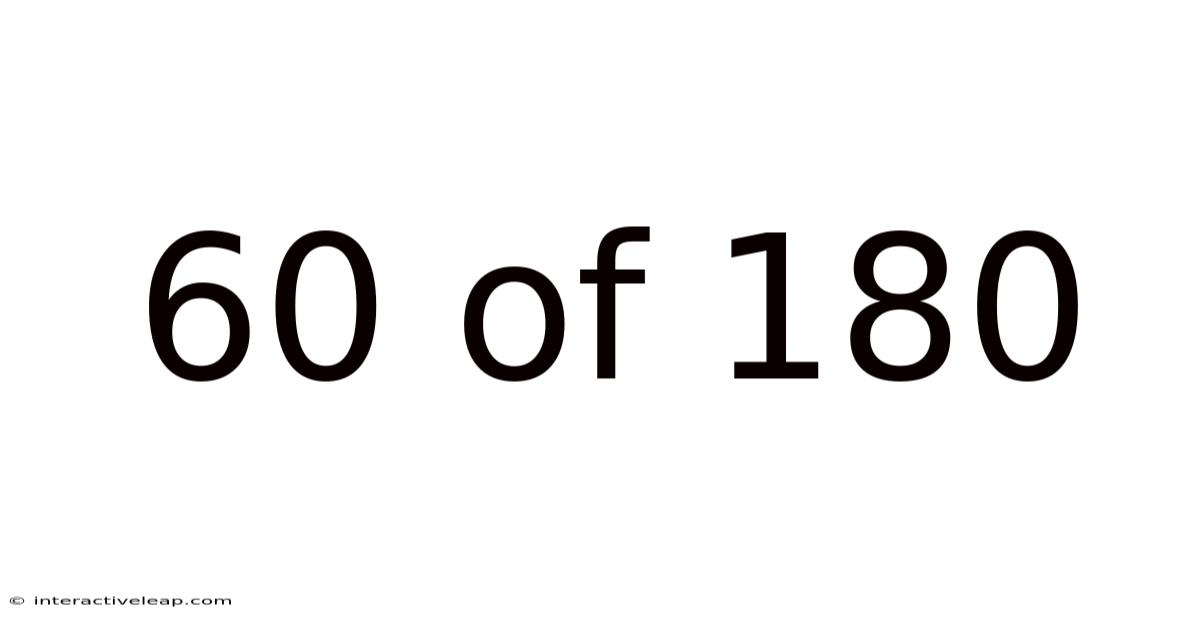
Table of Contents
Decoding the Fraction: Understanding 60/180 and its Implications
Understanding fractions is fundamental to mathematics and everyday life. This article delves deep into the seemingly simple fraction 60/180, exploring its simplification, real-world applications, and broader mathematical concepts it represents. We'll move beyond simple reduction to uncover the underlying principles and demonstrate its use in various contexts. This comprehensive guide is perfect for students, educators, and anyone looking to strengthen their fractional understanding.
I. Simplifying 60/180: A Step-by-Step Approach
The fraction 60/180 represents 60 parts out of a total of 180 parts. The most immediate step in working with this fraction is simplification. This involves finding the greatest common divisor (GCD) of the numerator (60) and the denominator (180), and then dividing both by that GCD.
Let's find the GCD of 60 and 180. Several methods exist:
-
Listing Factors: List the factors of both numbers and identify the largest common factor. The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. The factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180. The greatest common factor is 60.
-
Prime Factorization: Break down each number into its prime factors. 60 = 2² x 3 x 5 and 180 = 2² x 3² x 5. The GCD is found by multiplying the common prime factors raised to their lowest power: 2² x 3 x 5 = 60.
Once we know the GCD is 60, we can simplify the fraction:
60/180 = (60 ÷ 60) / (180 ÷ 60) = 1/3
Therefore, 60/180 simplifies to the equivalent fraction 1/3. This means that 60 out of 180 is the same as 1 out of 3.
II. Real-World Applications of 60/180 (or 1/3)
The fraction 1/3, derived from 60/180, appears frequently in various real-world situations:
-
Cooking and Baking: Recipes often call for fractions of ingredients. If a recipe requires 180g of flour and you only want to make 1/3 of the recipe, you would use (1/3) * 180g = 60g of flour.
-
Measurement and Geometry: Imagine a circle divided into 180 equal segments. 60 of these segments would represent 1/3 of the entire circle. This relates to angles and degrees, where 60 degrees is one-third of 180 degrees (a straight angle).
-
Probability and Statistics: If there are 180 possible outcomes in an experiment and 60 of those outcomes represent a specific event, the probability of that event occurring is 60/180 = 1/3.
-
Data Analysis: In analyzing data sets, you might find that 60 out of 180 respondents answered a survey question in a particular way. This would represent 1/3 of the total respondents.
-
Sharing and Division: If you need to divide 180 items equally among 3 people, each person receives 60 items, which is 1/3 of the total.
III. Expanding on the Concept: Fractions, Ratios, and Percentages
The fraction 60/180 (or 1/3) is not just a numerical value; it represents a ratio and can be expressed as a percentage.
-
Ratio: A ratio is a comparison of two quantities. The ratio 60:180 is equivalent to the ratio 1:3, indicating that for every 1 part of one quantity, there are 3 parts of another.
-
Percentage: To convert a fraction to a percentage, multiply the fraction by 100%. (1/3) * 100% ≈ 33.33%. Therefore, 60/180 represents approximately 33.33%.
IV. Connecting to Decimal Representation
Fractions can also be expressed as decimals. To convert 1/3 to a decimal, divide the numerator (1) by the denominator (3):
1 ÷ 3 ≈ 0.3333...
The decimal representation of 1/3 is a repeating decimal, indicated by the ellipsis (...). This means the digit 3 repeats infinitely.
V. Further Mathematical Explorations: Proportions and Equations
The fraction 60/180 can be used to solve proportions and equations. A proportion is a statement that two ratios are equal. For example:
60/180 = x/90
To solve for x, we can cross-multiply:
60 * 90 = 180 * x
5400 = 180x
x = 5400 / 180 = 30
This demonstrates how the relationship between 60 and 180 can be used to find an unknown value in a proportional relationship.
VI. Understanding Equivalent Fractions
It's crucial to grasp the concept of equivalent fractions. Equivalent fractions represent the same value, even though they have different numerators and denominators. 60/180, 30/90, 20/60, 10/30, and 1/3 are all equivalent fractions. They all simplify to the same simplest form: 1/3. Understanding this concept is essential for performing operations with fractions.
VII. Operations with Fractions: Addition, Subtraction, Multiplication, and Division
While we’ve focused on simplification, let's briefly touch upon operations involving fractions:
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. For example, adding 1/3 and 2/3 is straightforward: 1/3 + 2/3 = 3/3 = 1.
-
Multiplication: Multiplying fractions involves multiplying the numerators and then the denominators: (1/3) * (2/5) = 2/15.
-
Division: Dividing fractions involves inverting the second fraction and multiplying: (1/3) ÷ (2/5) = (1/3) * (5/2) = 5/6.
VIII. Advanced Concepts: Rational Numbers and Irrational Numbers
The fraction 60/180, and its simplified form 1/3, belong to the set of rational numbers. Rational numbers are numbers that can be expressed as the ratio of two integers (where the denominator is not zero). Irrational numbers, on the other hand, cannot be expressed as a ratio of two integers; examples include π (pi) and √2 (the square root of 2).
IX. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 60/180?
- A: The simplest form of 60/180 is 1/3.
-
Q: How do I convert 60/180 to a decimal?
- A: Divide 60 by 180, resulting in approximately 0.3333... (a repeating decimal).
-
Q: What is the percentage equivalent of 60/180?
- A: The percentage equivalent of 60/180 is approximately 33.33%.
-
Q: Are there other fractions equivalent to 60/180?
- A: Yes, many fractions are equivalent to 60/180, including 30/90, 20/60, 10/30, and so on. All of these simplify to 1/3.
-
Q: How can I use 60/180 in a real-world problem?
- A: Imagine you have 180 marbles and 60 are red. The fraction of red marbles is 60/180 = 1/3.
X. Conclusion: The Significance of Understanding Fractions
This in-depth exploration of the fraction 60/180 reveals its simplicity yet its significance in various mathematical and real-world contexts. From basic simplification to advanced concepts like rational numbers and proportions, this fraction serves as a stepping stone to a deeper understanding of fractional arithmetic. Mastering fractions is crucial for success in mathematics and for navigating many aspects of everyday life. The ability to simplify, compare, and perform operations with fractions is a skill that extends far beyond the classroom. Remember, the seemingly simple fraction 60/180 holds a wealth of mathematical principles and applications, making it a worthy subject of study.
Latest Posts
Latest Posts
-
Half Of 110
Sep 13, 2025
-
40 Off 55
Sep 13, 2025
-
13km In Miles
Sep 13, 2025
-
Painting A Waterfall
Sep 13, 2025
-
1 62cm In Feet
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.