6 X 4y
interactiveleap
Sep 25, 2025 · 6 min read
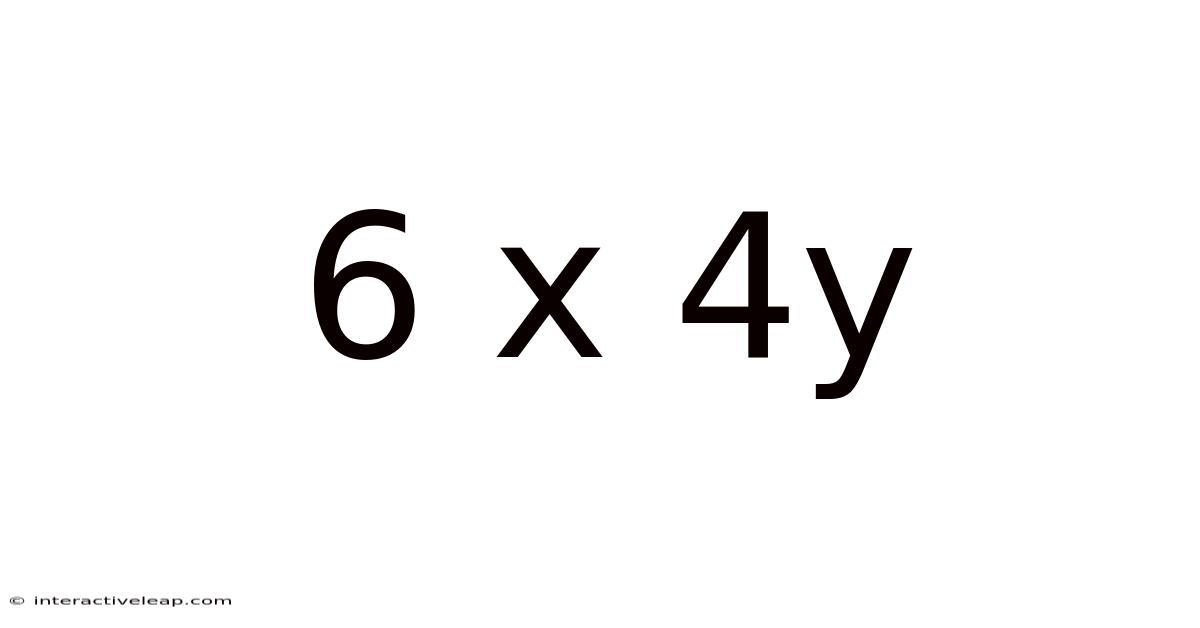
Table of Contents
Decoding 6 x 4y: A Deep Dive into Algebraic Expressions
This article explores the algebraic expression "6 x 4y," breaking down its components, explaining how to simplify and manipulate it, and demonstrating its applications in various mathematical contexts. Understanding this seemingly simple expression forms a crucial foundation for more advanced algebraic concepts. We'll cover everything from basic arithmetic to the principles behind combining like terms and solving for variables. Whether you're a student struggling with algebra or simply curious about the underlying logic, this comprehensive guide will equip you with the knowledge to confidently tackle similar expressions.
Introduction: Understanding the Basics
At first glance, "6 x 4y" might seem daunting, but it's fundamentally a combination of numbers and variables connected through multiplication. Let's break down each element:
- 6: This is a numerical coefficient, a constant value multiplying the rest of the expression.
- x: This is a variable, representing an unknown quantity. In algebra, variables are typically represented by letters from the alphabet.
- 4: This is another numerical coefficient.
- y: This is another variable, potentially representing a different unknown quantity than 'x'.
- x and 4y: The 'x' and '4y' are considered terms of the expression, separated by implied multiplication.
The expression signifies the multiplication of 6 with the product of 4 and y, further multiplied by x. The multiplication symbol 'x' is often omitted for brevity, so the expression can be written as 6(4y)x or 6 * 4 * y * x, but the order of multiplication remains crucial.
Simplifying the Expression: Combining Like Terms
The expression "6 x 4y" can be simplified using the commutative and associative properties of multiplication. These properties allow us to rearrange the numbers and variables without changing the overall value of the expression.
The commutative property states that the order of multiplication doesn't affect the result (a x b = b x a). The associative property states that the grouping of multiplication doesn't affect the result ((a x b) x c = a x (b x c)).
Applying these properties:
-
Rearrange the terms: We can rearrange the expression as 6 x 4 x x x y.
-
Multiply the coefficients: Multiply the numerical coefficients: 6 x 4 = 24.
-
Combine the variables: Combine the variables: x x x = x². (This uses the rule of exponents: x¹ * x¹ = x¹⁺¹ = x²)
-
Simplified expression: The simplified expression becomes 24x²y.
Therefore, 6 x 4y, when fully simplified, is equivalent to 24x²y. This simplified form is more concise and easier to work with in further calculations or problem-solving.
Expanding the Expression: Distributive Property
While the original expression doesn't explicitly demonstrate the distributive property, understanding this property is essential for working with similar algebraic expressions. The distributive property states that a(b + c) = ab + ac. Consider a slightly modified scenario: 6x(4y + 2z). Here's how the distributive property would be applied:
-
Distribute 6x to both terms within the parentheses: 6x(4y) + 6x(2z)
-
Simplify each term: 24xy + 12xz
Therefore, 6x(4y + 2z) simplifies to 24xy + 12xz. This example illustrates how the distributive property helps to expand and simplify expressions involving parentheses and multiple variables.
Solving for Variables: Introduction to Equations
The expression "6 x 4y" itself doesn't represent an equation; it's simply an algebraic expression. To solve for a variable, we need an equation, which is a statement indicating that two expressions are equal. For instance, let's consider the equation:
6 x 4y = 48
To solve for 'y', we follow these steps:
-
Simplify the left side: The left side simplifies to 24y (as shown previously).
-
Rewrite the equation: The equation becomes 24y = 48.
-
Isolate the variable: Divide both sides of the equation by 24 to isolate 'y': y = 48 / 24
-
Solution: y = 2
Therefore, in the equation 6 x 4y = 48, the value of 'y' is 2. This demonstrates how simplifying expressions is crucial for solving equations.
Applications in Real-World Scenarios
Algebraic expressions like "6 x 4y" might seem abstract, but they have many practical applications in various fields:
-
Geometry: Calculating the area of a rectangle with sides 6x and 4y would result in an area of 24xy square units.
-
Physics: In physics problems involving forces, velocities, or accelerations, such expressions often arise. For example, calculating the total momentum of two objects.
-
Engineering: In engineering design and calculations, these expressions are frequently used to represent quantities and their relationships.
-
Economics: Economic models often utilize algebraic expressions to model relationships between variables like supply, demand, and price.
-
Computer Programming: These expressions are fundamental to computer programming, where they're used to perform calculations and manipulate data.
Advanced Concepts: Polynomials and Beyond
The expression "24x²y" (the simplified version of 6 x 4y) is a type of polynomial. Specifically, it's a monomial because it contains only one term. Polynomials are algebraic expressions that consist of variables and coefficients, involving only the operations of addition, subtraction, and multiplication. They can have multiple terms, such as 3x² + 2xy - 5y³. Understanding monomials and polynomials is essential for more advanced algebraic manipulation, including factoring, expanding, and solving polynomial equations.
Frequently Asked Questions (FAQ)
Q: What is the difference between a coefficient and a variable?
A: A coefficient is a numerical constant that multiplies a variable. A variable is a symbol (usually a letter) that represents an unknown or changing quantity. In "6x," 6 is the coefficient, and x is the variable.
Q: Can I change the order of multiplication in an algebraic expression?
A: Yes, due to the commutative and associative properties of multiplication, you can rearrange the terms in a multiplication expression without changing its value.
Q: What happens if I have an expression like 6 x 4y + 2?
A: In this case, you would simplify the multiplication part first (resulting in 24y) and then you'd have the expression 24y + 2. You can't simplify further because 'y' and 2 are not like terms.
Q: How do I solve for more than one variable in an equation?
A: Solving for multiple variables usually requires a system of equations (multiple equations with the same variables). You can use methods like substitution or elimination to solve for the variables.
Conclusion: Mastering Algebraic Expressions
Understanding and manipulating algebraic expressions like "6 x 4y" is a fundamental skill in mathematics. This seemingly simple expression embodies key concepts such as variables, coefficients, the commutative and associative properties of multiplication, and the distributive property. By mastering these principles and practicing simplification techniques, you build a strong foundation for tackling more complex algebraic problems and equations. The applications of such skills extend far beyond the classroom, proving essential in various scientific, engineering, and computational fields. Remember that consistent practice and a clear understanding of the underlying principles are keys to success in algebra and beyond.
Latest Posts
Latest Posts
-
38 Years Ago
Sep 25, 2025
-
Categories Of Planning
Sep 25, 2025
-
0 08 In Percent
Sep 25, 2025
-
1 Of 25
Sep 25, 2025
-
3 Syllable Nouns
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 6 X 4y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.