56 Of 850
interactiveleap
Sep 14, 2025 · 5 min read
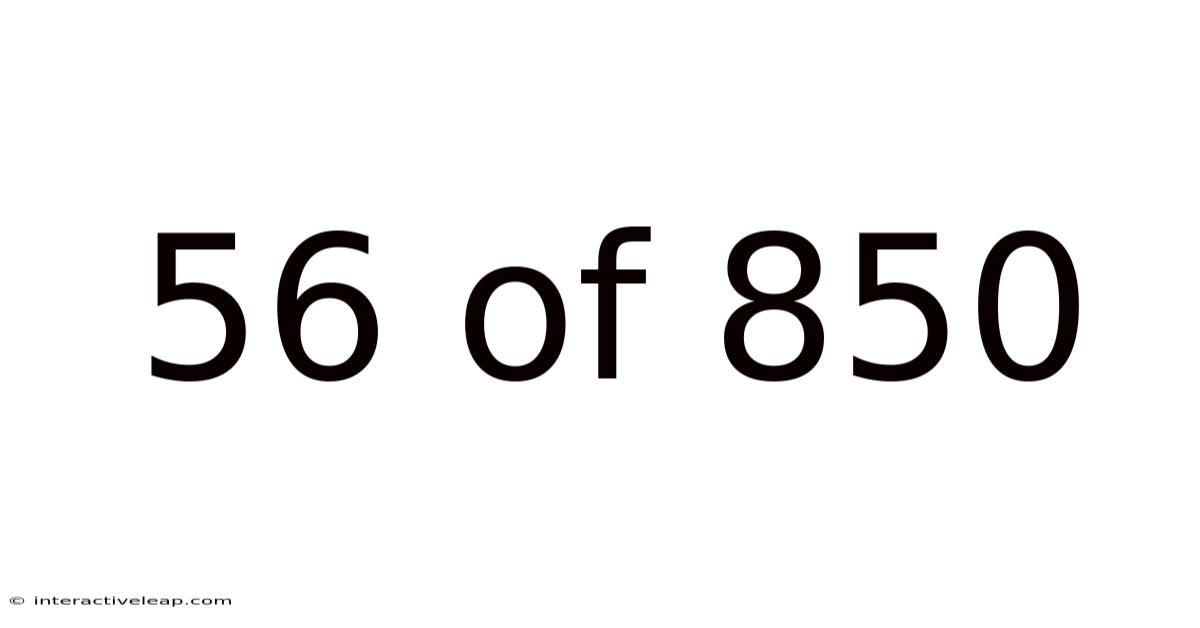
Table of Contents
Decoding the Fraction: Understanding 56 out of 850
The seemingly simple fraction 56/850 represents more than just a numerical value; it encapsulates a fundamental concept in mathematics and has wide-ranging applications in various fields. Understanding this fraction, and its implications, requires delving into the world of ratios, percentages, and proportional reasoning. This article will provide a comprehensive exploration of 56/850, examining its simplification, its representation as a percentage, its applications, and addressing common questions surrounding such fractional representations.
Simplifying the Fraction: Finding the Lowest Terms
The first step in understanding 56/850 is to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator (56) and the denominator (850) and dividing both by that number.
Let's find the GCD of 56 and 850. We can use the Euclidean algorithm or prime factorization. Using prime factorization:
- 56 = 2 x 2 x 2 x 7 = 2³ x 7
- 850 = 2 x 5 x 5 x 17 = 2 x 5² x 17
The only common factor is 2. Therefore, we divide both the numerator and the denominator by 2:
56 ÷ 2 = 28 850 ÷ 2 = 425
Therefore, the simplified fraction is 28/425. This simplified form is much easier to work with and understand than the original fraction.
Converting to a Percentage: Expressing the Fraction as a Proportion
Converting a fraction to a percentage provides a more intuitive understanding of the fraction's relative size. To convert 28/425 to a percentage, we perform the division and multiply by 100:
28 ÷ 425 ≈ 0.06588
Multiplying by 100 gives us approximately 6.59%. This means that 56 out of 850 represents approximately 6.59% of the whole. This percentage representation is invaluable in various contexts, allowing for easier comparison and interpretation.
Real-World Applications: Where Does This Fraction Arise?
The fraction 56/850, or its simplified form 28/425, can appear in numerous real-world scenarios. Consider these examples:
-
Test Scores: Imagine a student scoring 56 out of 850 points on a comprehensive exam. The percentage score (approximately 6.59%) provides a clear picture of their performance relative to the total possible score. This helps in evaluating the student's understanding of the subject matter.
-
Survey Results: In a survey of 850 people, 56 responded positively to a particular question. The fraction 56/850, converted to a percentage, helps in representing the proportion of positive responses within the surveyed population. This data is vital for market research, opinion polls, and other statistical analyses.
-
Manufacturing Defects: A factory produces 850 units of a product, and 56 are found to be defective. The fraction 56/850 helps determine the defect rate. This is crucial for quality control and improving manufacturing processes.
-
Financial Analysis: Suppose a company's total assets are 850 million dollars, and 56 million dollars are allocated to a specific investment. The fraction 56/850 indicates the proportion of total assets invested in that particular area. This aids in assessing investment strategies and risk management.
-
Scientific Experiments: In scientific experiments involving large datasets, fractions like 56/850 might represent the proportion of successful trials or the frequency of a particular event. These fractions form the basis for statistical analysis and drawing conclusions from the experimental data.
Deeper Dive: Understanding Ratios and Proportions
The fraction 56/850 can also be understood as a ratio. A ratio compares two quantities. In this case, the ratio is 56:850, or 28:425 in its simplest form. This ratio represents the relationship between the two quantities.
Proportions extend the concept of ratios. A proportion is a statement that two ratios are equal. For instance, we can set up a proportion to find an unknown quantity. Let's say we want to know how many items would be represented by 14 in the ratio 28:425. We can set up the proportion:
28/425 = 14/x
Solving for x, we get:
x = (14 * 425) / 28 = 212.5
This shows the power of proportions in scaling up or down quantities based on a known ratio.
Illustrative Examples and Problem Solving
Let's explore some examples to further solidify our understanding:
Example 1: A school has 850 students. If 56 students participate in a school play, what percentage of the student body participates?
- Solution: This is directly represented by the fraction 56/850. Converting to a percentage as shown earlier, approximately 6.59% of the student body participates in the school play.
Example 2: A farmer harvested 850 apples. 28 of them were bruised and unsuitable for sale. What is the ratio of bruised apples to total apples harvested?
- Solution: The ratio is 28:850, which simplifies to 14:425. This represents the proportion of bruised apples compared to the total harvest.
Example 3: If a recipe calls for 28 grams of sugar for 425 grams of flour, how much sugar would be needed for 850 grams of flour?
- Solution: This is a proportion problem. Setting up the proportion: 28/425 = x/850. Solving for x gives x = 56 grams of sugar.
Frequently Asked Questions (FAQ)
Q: Can 56/850 be expressed as a decimal?
A: Yes, 56/850, or its simplified form 28/425, is approximately equal to 0.06588.
Q: What is the simplest form of 56/850?
A: The simplest form is 28/425.
Q: How do I convert 28/425 to a percentage?
A: Divide 28 by 425 and then multiply by 100. This yields approximately 6.59%.
Q: What are the practical applications of understanding this fraction?
A: Understanding this fraction helps in various fields, including assessing test scores, analyzing survey results, evaluating manufacturing defects, performing financial analysis, and conducting scientific experiments, among others.
Conclusion: The Significance of Understanding Fractions
The fraction 56/850, seemingly insignificant at first glance, reveals the power of mathematical concepts like simplification, percentage conversion, ratios, and proportions. Understanding these concepts allows us to interpret data effectively, solve problems efficiently, and make informed decisions in various aspects of life. This article has provided a comprehensive exploration of this fraction, highlighting its various interpretations and practical applications. By mastering the principles discussed here, you equip yourself with valuable tools for navigating the quantitative world around us. Remember that seemingly small numbers can hold significant meaning when viewed through the lens of mathematical understanding.
Latest Posts
Latest Posts
-
35pounds To Kg
Sep 14, 2025
-
70 Of 65
Sep 14, 2025
-
Lee Friedlander Photographer
Sep 14, 2025
-
300pounds In Kg
Sep 14, 2025
-
147 Pounds Kg
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 56 Of 850 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.