56 Of 80
interactiveleap
Sep 20, 2025 · 5 min read
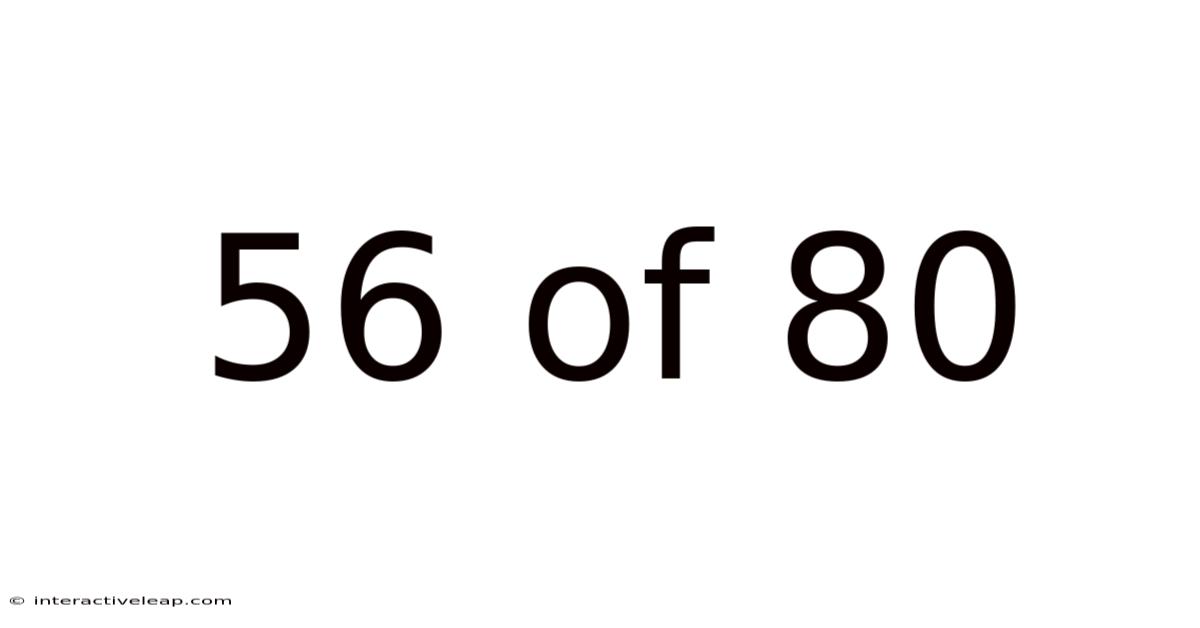
Table of Contents
Decoding the Fraction: Understanding 56 out of 80
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in everyday life and advanced studies. This article delves deep into the meaning and implications of the fraction 56 out of 80, exploring its simplification, percentage representation, practical applications, and the broader context of fractional understanding. We'll break down the concepts in a clear, accessible manner, ensuring that even those with limited mathematical backgrounds can grasp the core principles.
Introduction: What Does 56 out of 80 Mean?
The fraction "56 out of 80" represents a part-to-whole relationship. It signifies that we have 56 items out of a total of 80 items. This is a common way to express a proportion or ratio. Understanding this seemingly simple fraction opens doors to a world of mathematical calculations and real-world applications, from calculating test scores to understanding statistical data.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before delving into deeper analysis, simplifying the fraction makes it easier to understand and work with. This involves finding the greatest common divisor (GCD) of both the numerator (56) and the denominator (80). The GCD is the largest number that divides both numbers without leaving a remainder.
To find the GCD, we can use several methods, including prime factorization:
- Prime Factorization of 56: 2 x 2 x 2 x 7 (2³ x 7)
- Prime Factorization of 80: 2 x 2 x 2 x 2 x 5 (2⁴ x 5)
The common factors are 2 x 2 x 2 = 8. Therefore, the GCD of 56 and 80 is 8.
Now, we simplify the fraction by dividing both the numerator and denominator by the GCD:
56 ÷ 8 = 7 80 ÷ 8 = 10
Thus, the simplified fraction is 7/10. This simplified form is much easier to work with in subsequent calculations and provides a clearer representation of the proportion.
Converting to Percentage: Expressing the Fraction as a Percentage
Converting a fraction to a percentage provides another way of understanding the proportion. To do this, we divide the numerator by the denominator and then multiply by 100:
(7 ÷ 10) x 100 = 70%
Therefore, 56 out of 80 represents 70%. This percentage representation offers a readily understandable and commonly used measure of proportion. It's easy to grasp that 70% signifies a significant portion of the whole.
Practical Applications: Real-World Examples of 56 out of 80
The fraction 56 out of 80, or its simplified form 7/10, and its percentage equivalent of 70%, find application in numerous real-world scenarios:
- Academic Performance: If a student answered 56 questions correctly out of 80 on a test, their score is 70%. This provides a clear measure of their performance.
- Sales Targets: A salesperson who achieves 56 sales out of a target of 80 has achieved 70% of their goal. This information is vital for performance evaluation.
- Project Completion: If 56 tasks out of 80 planned tasks are completed in a project, the project is 70% complete. This is crucial for progress tracking.
- Statistical Data: In surveys or data analysis, 56 responses out of 80 represent 70% of the sample. This percentage can then be used for broader inferences.
- Manufacturing: If 56 out of 80 products pass quality control, the pass rate is 70%. This data is critical for maintaining quality standards.
Understanding the Concept of Proportion and Ratio
The fraction 56 out of 80 exemplifies the concepts of proportion and ratio. A ratio is a comparison between two quantities, while a proportion is a statement of equality between two ratios.
In this case, the ratio is 56:80, which simplifies to 7:10. A proportion could be expressed as 56/80 = 7/10 = 70/100. These different representations all convey the same fundamental relationship.
Further Mathematical Exploration: Decimals and Beyond
The fraction 7/10 can also be expressed as a decimal: 0.7. This decimal representation is another useful way to represent the proportion. It allows for easy comparison and calculation with other decimal numbers.
Furthermore, the understanding of fractions like 56/80 forms the foundation for more advanced mathematical concepts like:
- Probability: The likelihood of an event occurring can be expressed as a fraction.
- Algebra: Fractions are integral to algebraic equations and manipulations.
- Calculus: Fractional concepts are crucial in differential and integral calculus.
Frequently Asked Questions (FAQ)
-
Q: How do I convert a percentage to a fraction?
- A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 70% becomes 70/100, which simplifies to 7/10.
-
Q: What if I have a fraction with a larger numerator than denominator?
- A: This is called an improper fraction. It can be converted into a mixed number, which consists of a whole number and a proper fraction. For example, 80/56 would be simplified to 10/7, then converted to the mixed number 1 3/7.
-
Q: Are there other methods to find the GCD?
- A: Yes, the Euclidean algorithm is another efficient method for finding the GCD of two numbers.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It provides a more concise and efficient representation of the proportion.
Conclusion: The Significance of Fractional Understanding
The seemingly simple fraction 56 out of 80 provides a rich learning opportunity. Its analysis encompasses simplification, percentage conversion, real-world applications, and fundamental mathematical concepts like ratios and proportions. Mastering fractional understanding is not just about solving mathematical problems; it is about developing a crucial skill set applicable across diverse disciplines and everyday situations. From analyzing test scores to understanding project progress, the ability to interpret and manipulate fractions is essential for navigating the complexities of the numerical world. Therefore, a thorough grasp of this fundamental concept is a valuable asset for anyone seeking to enhance their mathematical literacy and problem-solving abilities. The journey from "56 out of 80" to 70% and further to a deeper understanding of proportions and ratios is a testament to the power of mathematical reasoning and its far-reaching implications.
Latest Posts
Latest Posts
-
1 75 X 4
Sep 20, 2025
-
Half Of 49
Sep 20, 2025
-
150lbs En Kg
Sep 20, 2025
-
Cecil J Sharp
Sep 20, 2025
-
30 Of 360
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 56 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.