5000 / 3
interactiveleap
Sep 14, 2025 · 5 min read
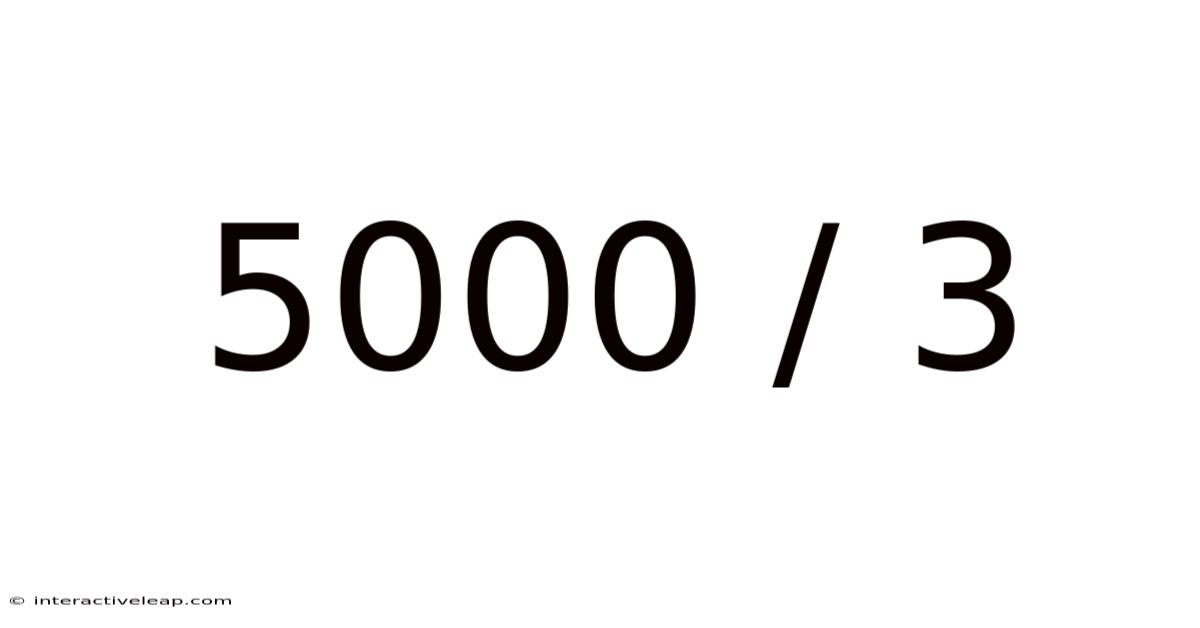
Table of Contents
Decoding 5000 / 3: A Deep Dive into Division and its Applications
This article explores the seemingly simple mathematical operation of 5000 divided by 3, delving beyond the immediate answer to uncover the underlying principles of division, its various applications across diverse fields, and the broader implications within the context of mathematics and beyond. Understanding this seemingly basic calculation unlocks a world of mathematical concepts and their real-world relevance. We'll unpack the process, explore different methods of calculation, and investigate the practical uses of division in everyday life, science, and engineering.
Understanding Division: More Than Just Sharing
Division, at its core, is the inverse operation of multiplication. While multiplication involves combining equal groups, division involves separating a quantity into equal groups or determining how many times one quantity is contained within another. The expression 5000 / 3 asks: "If we have 5000 units and we want to divide them into 3 equal groups, how many units will be in each group?" This seemingly straightforward question leads to a deeper understanding of fractions, decimals, and the concept of remainders.
Calculating 5000 / 3: Methods and Approaches
Several methods can be used to calculate 5000 / 3. Let's explore some common approaches:
1. Long Division: This classic method is a fundamental skill taught in elementary education. It involves a step-by-step process of dividing, multiplying, subtracting, and bringing down digits.
1666
3 | 5000
-3
20
-18
20
-18
20
-18
2
The long division shows that 5000 divided by 3 is 1666 with a remainder of 2. This means that 5000 can be divided into three groups of 1666, with two units left over.
2. Using a Calculator: The simplest method is to use a calculator. Simply input "5000 / 3" and the calculator will provide the answer: 1666.666... (the decimal continues infinitely).
3. Fractions: We can express the result as a fraction: 5000/3. This fraction is an improper fraction because the numerator (5000) is larger than the denominator (3). It can be converted to a mixed number: 1666 ⅔. This represents 1666 whole groups and two-thirds of another group.
Interpreting the Result: Remainders and Decimals
The remainder of 2 in the long division highlights an important aspect of division: not all divisions result in whole numbers. When the dividend (5000) is not perfectly divisible by the divisor (3), a remainder is obtained. This remainder represents the portion that cannot be equally distributed among the groups.
The decimal representation (1666.666...) provides another perspective. The repeating decimal 6 signifies that the division continues infinitely, with the fraction ⅔ representing the continuous remainder. This is a recurring decimal and highlights the relationship between fractions and decimals.
Applications of Division: From Everyday Life to Advanced Science
The seemingly simple calculation of 5000 / 3 has far-reaching applications in various fields:
1. Everyday Life:
- Sharing Resources: Dividing resources among people, such as splitting a bill equally among friends, distributing candies among children, or allocating tasks amongst team members, often involves division.
- Measurement and Conversion: Converting units of measurement, such as converting kilometers to miles or pounds to kilograms, frequently requires division.
- Pricing and Discounts: Calculating the price per unit or the percentage discount often involves division. For example, if 3 items cost 5000, the cost per item is 5000 / 3.
2. Science and Engineering:
- Averaging Data: In scientific experiments, calculating the average of multiple measurements involves summing the values and dividing by the number of measurements.
- Physics and Engineering Calculations: Numerous physics and engineering formulas involve division. Examples include calculating speed (distance/time), density (mass/volume), and acceleration.
- Computer Science: Division plays a crucial role in algorithms and computer programming, particularly in tasks involving data structures, sorting, and searching.
3. Finance and Economics:
- Calculating Averages: Averaging financial data like stock prices, investment returns, or economic growth rates frequently utilizes division.
- Profit and Loss Calculations: Determining profit margins or loss percentages requires division.
- Interest Calculation: Calculating simple or compound interest involves division.
4. Statistics:
- Calculating Averages and Frequencies: Finding the mean, median, and mode in a dataset involves division and other mathematical operations.
- Probability Calculations: Many probability problems require division to determine the likelihood of events occurring.
Beyond the Numbers: The Importance of Conceptual Understanding
While the numerical answer to 5000 / 3 is readily obtainable, the true value lies in comprehending the underlying mathematical concepts. Understanding division goes beyond rote calculation; it fosters critical thinking and problem-solving abilities. It helps us to:
- Interpret Remainders: Understand the significance of remainders and their implications in different contexts.
- Work with Fractions and Decimals: Develop fluency in converting between fractions, decimals, and mixed numbers.
- Apply Mathematical Principles: Translate real-world problems into mathematical expressions and solve them effectively.
- Develop Problem-Solving Skills: Improve analytical and critical thinking skills through the application of mathematical concepts.
Frequently Asked Questions (FAQ)
Q: What is the exact answer to 5000 / 3?
A: The exact answer is 1666 ⅔, or 1666.666... (a recurring decimal).
Q: Why is there a remainder when 5000 is divided by 3?
A: Because 5000 is not perfectly divisible by 3. The remainder represents the portion that cannot be equally divided among the three groups.
Q: How can I check my answer?
A: You can check your answer by multiplying the quotient (1666) by the divisor (3) and adding the remainder (2). The result should be the dividend (5000): 1666 * 3 + 2 = 5000.
Q: What are some real-world examples where this calculation might be used?
A: Examples include dividing a total cost among three people, calculating the average of three measurements in a science experiment, or determining the price per unit if three items cost 5000.
Conclusion: The Enduring Power of Division
The seemingly simple calculation of 5000 / 3 offers a gateway to a deeper understanding of division, its various methods, and its vast applications across diverse fields. Beyond the numerical answer, the importance lies in grasping the underlying concepts, interpreting the results, and applying this foundational mathematical skill to solve real-world problems. The ability to perform and interpret division is not just a mathematical skill; it is a critical thinking tool with broad implications in various aspects of life, from everyday tasks to complex scientific and engineering challenges. The journey from understanding the basic arithmetic to appreciating its practical uses is a testament to the power and relevance of mathematics in our world.
Latest Posts
Latest Posts
-
41kg To Pounds
Sep 14, 2025
-
20 35 Simplified
Sep 14, 2025
-
Megalodon Comparison Size
Sep 14, 2025
-
Autumn In Spanish
Sep 14, 2025
-
20 Of 380
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 5000 / 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.