50 X 0.2
interactiveleap
Sep 24, 2025 · 5 min read
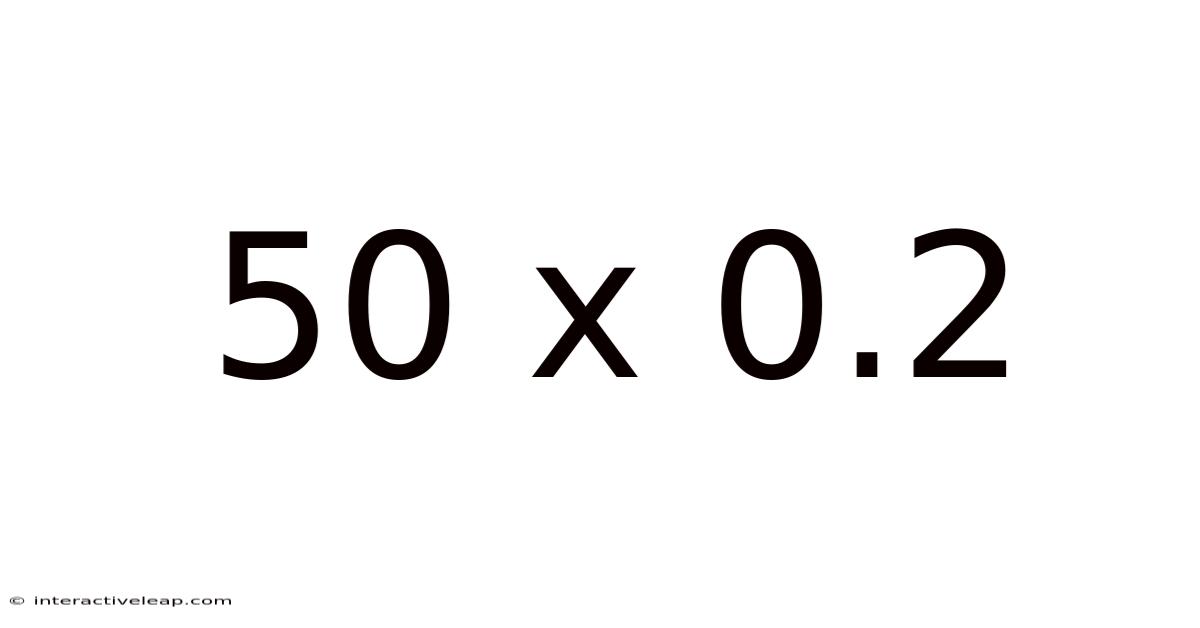
Table of Contents
Decoding 50 x 0.2: A Deep Dive into Multiplication and Decimal Numbers
This article explores the seemingly simple calculation of 50 x 0.2, delving beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll examine different methods of solving this problem, explain the concept of decimal multiplication, and discuss its relevance in various real-world scenarios. Understanding this seemingly basic calculation is crucial for mastering more complex mathematical concepts and problem-solving skills.
Understanding the Fundamentals: Multiplication and Decimals
Before we tackle 50 x 0.2, let's refresh our understanding of the core concepts involved: multiplication and decimal numbers.
Multiplication is a fundamental arithmetic operation that represents repeated addition. For example, 5 x 3 means adding 5 three times (5 + 5 + 5 = 15). It's a crucial tool for calculating quantities, scaling values, and understanding proportions.
Decimal numbers are numbers that include a decimal point, separating the whole number part from the fractional part. The digits to the right of the decimal point represent fractions of a whole. For example, 0.2 is equivalent to 2/10 or 1/5. Understanding decimals is vital for working with fractions, percentages, and measurements in various fields.
Method 1: Direct Multiplication
The most straightforward way to solve 50 x 0.2 is through direct multiplication. We can write the problem vertically:
50
x 0.2
------
Multiplying as if the decimal point wasn't there:
50
x 2
------
100
Now, we account for the decimal point. In 0.2, the decimal point is one place to the left of the units digit. Therefore, we move the decimal point in the answer one place to the left:
10.0
Therefore, 50 x 0.2 = 10.
Method 2: Converting to Fractions
Another effective approach is to convert the decimal number into a fraction. 0.2 is equivalent to 2/10, which can be simplified to 1/5. The calculation then becomes:
50 x (1/5) = 50/5 = 10
This method highlights the relationship between decimals and fractions, offering a different perspective on the calculation. It's particularly helpful when working with more complex decimal numbers that might not be easily multiplied directly.
Method 3: Using Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. We can use this property to break down the calculation:
We can rewrite 50 as 5 x 10. Thus, the calculation becomes:
(5 x 10) x 0.2 = 5 x (10 x 0.2) = 5 x 2 = 10
This method showcases the flexibility of applying mathematical properties to simplify calculations.
Method 4: Understanding Percentages
Since 0.2 is equivalent to 20%, the calculation can also be interpreted as finding 20% of 50.
To find 20% of 50, we can calculate:
(20/100) x 50 = 10
This method emphasizes the connection between decimals, fractions, and percentages, offering a practical application in real-world scenarios involving discounts, taxes, or proportions.
Real-World Applications of 50 x 0.2
The calculation 50 x 0.2, while seemingly simple, has numerous applications in everyday life and various professions:
-
Shopping Discounts: If an item costs $50 and is discounted by 20%, the discount amount is 50 x 0.2 = $10.
-
Tax Calculations: If a sales tax is 20%, the tax amount on a $50 purchase is 50 x 0.2 = $10.
-
Financial Calculations: Calculating interest, profit margins, or commission often involves similar decimal multiplications. For instance, if an investment yields a 20% return on a $50 investment, the return is $10.
-
Scientific Calculations: Many scientific formulas and calculations utilize decimal multiplication. For example, converting units or scaling measurements often involve multiplying by decimal values.
-
Engineering and Design: Proportions and scaling in engineering and design frequently require calculations like 50 x 0.2, ensuring that components are appropriately sized and scaled.
-
Data Analysis: Working with datasets often involves calculations involving percentages and proportions, leading to multiplications with decimals.
Expanding the Concept: Working with Larger and More Complex Decimals
While 50 x 0.2 is relatively straightforward, the principles we've discussed apply to more complex calculations involving larger numbers and decimals with more digits after the decimal point. For example:
-
125 x 0.35: This calculation can be approached using the same methods: direct multiplication, converting to fractions (125 x 35/100), or utilizing the distributive property.
-
250 x 0.04: Similar methods can be applied, highlighting the importance of understanding place value and decimal placement.
-
Calculations with more decimal places: Even with decimal numbers containing multiple digits after the decimal point, the same principles of multiplication and decimal placement remain consistent.
Frequently Asked Questions (FAQ)
Q1: Why do we move the decimal point when multiplying by a decimal?
A1: Moving the decimal point accounts for the fractional part of the decimal number. Multiplying by 0.2 is the same as multiplying by 2/10. The decimal point shift reflects the division by 10 (or a power of 10 depending on the number of decimal places).
Q2: What if I multiply 50 by 0.2 and get a different answer?
A2: Double-check your multiplication steps. Ensure you've correctly lined up the numbers and accurately accounted for the decimal point in the final answer. Using a calculator can help verify your calculations.
Q3: Are there other ways to solve 50 x 0.2?
A3: Yes, you can use mental math techniques, estimation, or specialized calculators depending on the context and desired level of precision.
Q4: How important is it to master this type of calculation?
A4: Mastering decimal multiplication is crucial for success in mathematics, science, and numerous professions. It forms the foundation for understanding more complex mathematical concepts and problem-solving skills.
Conclusion: Beyond the Calculation
The seemingly simple calculation of 50 x 0.2 provides a gateway to understanding fundamental mathematical principles. By exploring different methods of solving this problem, we've uncovered the importance of mastering multiplication, decimal numbers, fractions, and percentages. These concepts form the bedrock of numerous real-world applications, ranging from everyday shopping to complex scientific calculations. The ability to accurately and efficiently perform these calculations not only improves mathematical proficiency but also enhances problem-solving skills crucial across various disciplines and everyday life. Remember, consistent practice and a thorough understanding of the underlying principles are key to mastering this and more complex mathematical operations.
Latest Posts
Latest Posts
-
1 7m To Ft
Sep 24, 2025
-
Adult Snorkel Set
Sep 24, 2025
-
Durer Melencolia I
Sep 24, 2025
-
Barium Flame Test
Sep 24, 2025
-
Describe Haunted House
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 50 X 0.2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.