50 Of 2500
interactiveleap
Sep 24, 2025 · 5 min read
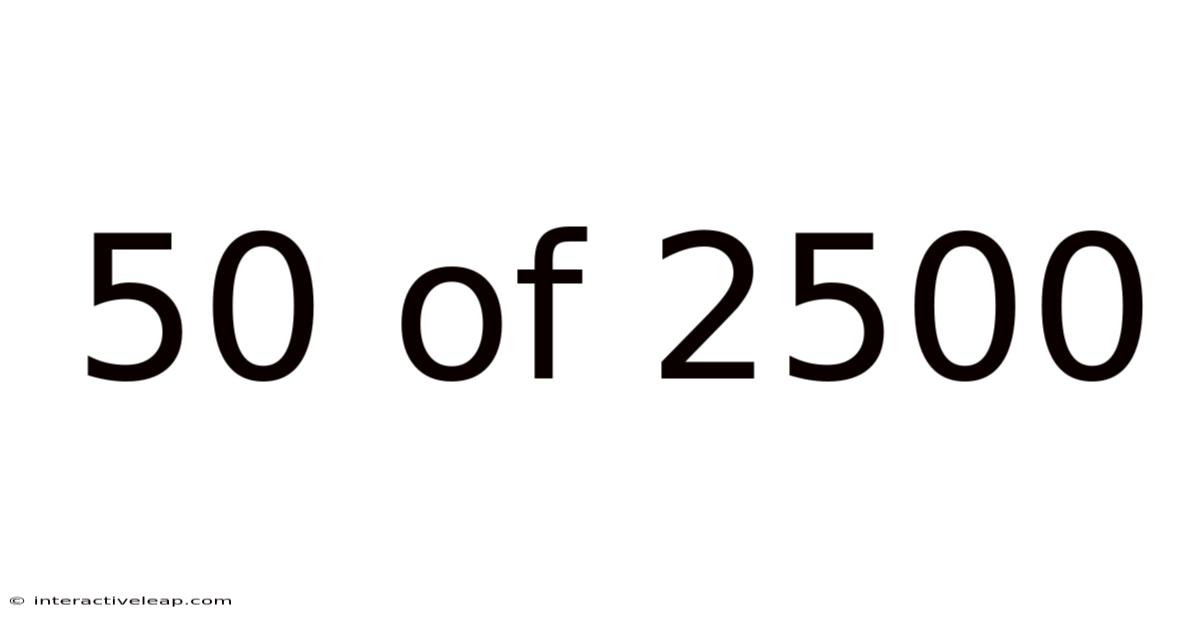
Table of Contents
Understanding the Fraction 50/2500: A Deep Dive into Simplification and Applications
The fraction 50/2500 might seem intimidating at first glance, especially for those less comfortable with mathematics. However, understanding this fraction is not only achievable but also reveals fundamental concepts in simplifying fractions and their practical applications in various fields. This article will guide you through a comprehensive exploration of 50/2500, covering its simplification, decimal equivalent, percentage representation, and real-world examples. We'll also delve into the broader mathematical principles behind fraction simplification and address frequently asked questions.
Introduction: Deconstructing 50/2500
The fraction 50/2500 represents a part-to-whole relationship. The numerator (50) indicates the number of parts considered, while the denominator (2500) represents the total number of equal parts that make up the whole. At its core, this fraction implies a proportion or ratio. Understanding how to simplify this fraction, convert it to a decimal, and express it as a percentage is crucial for numerous applications, from everyday calculations to complex scientific analyses.
Simplifying 50/2500: Finding the Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its lowest terms. This is done by finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by that GCD. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's find the GCD of 50 and 2500. We can use several methods, including prime factorization or the Euclidean algorithm. For simplicity, let's use prime factorization:
- Prime factorization of 50: 2 x 5 x 5 = 2 x 5²
- Prime factorization of 2500: 2 x 2 x 5 x 5 x 5 x 5 = 2² x 5⁴
The common factors are 2 and 5². Therefore, the GCD is 2 x 5² = 50.
Now, we divide both the numerator and denominator by the GCD:
50 ÷ 50 = 1 2500 ÷ 50 = 50
Therefore, the simplified fraction is 1/50. This simpler form makes it much easier to understand and use in calculations.
Converting 1/50 to a Decimal and Percentage
Once we have the simplified fraction, converting it to a decimal and a percentage is straightforward:
-
Decimal: To convert a fraction to a decimal, divide the numerator by the denominator: 1 ÷ 50 = 0.02
-
Percentage: To convert a decimal to a percentage, multiply by 100: 0.02 x 100 = 2%
Therefore, 50/2500 is equivalent to 0.02 as a decimal and 2% as a percentage.
Real-World Applications of 50/2500 (and its simplified form 1/50)
The fraction 50/2500, or its simplified equivalent 1/50, appears in various real-world scenarios:
-
Surveys and Statistics: Imagine a survey of 2500 people where 50 responded positively to a particular question. The fraction 50/2500 (or 2%) represents the proportion of positive responses.
-
Financial Calculations: If you invest $2500 and earn $50 in interest, your return is 50/2500, or 2% of your investment.
-
Manufacturing and Quality Control: If a factory produces 2500 units and 50 are defective, the defect rate is 50/2500, or 2%.
-
Scientific Experiments: In experiments involving measurements and data analysis, representing proportions as fractions is common. 50/2500, or its simplified form, can represent the ratio of a specific outcome to the total number of trials.
-
Mixing Solutions: In chemistry or cooking, accurately measuring ingredients is crucial. A recipe that calls for a small amount of ingredient relative to the total volume might be expressed as a fraction like 1/50.
Further Exploration: Understanding Fraction Simplification
The process of simplifying fractions, as demonstrated above, relies on several core mathematical concepts:
-
Factors and Multiples: Understanding factors (numbers that divide evenly into another number) and multiples (products of a number and another integer) is essential for finding the GCD.
-
Prime Numbers: Prime numbers (numbers divisible only by 1 and themselves) play a key role in prime factorization, a method used to find the GCD.
-
Greatest Common Divisor (GCD): As discussed, the GCD is the largest number that divides both the numerator and denominator. Efficiently finding the GCD is critical for simplifying fractions.
-
Equivalent Fractions: Simplifying a fraction doesn't change its value; it merely represents the same proportion in a simpler form. 1/50 is equivalent to 50/2500, even though they look different. This concept of equivalent fractions is fundamental in algebra and other branches of mathematics.
Frequently Asked Questions (FAQ)
-
Q: Can I simplify 50/2500 any further than 1/50?
A: No. 1/50 is in its simplest form because the GCD of 1 and 50 is 1.
-
Q: What if the numerator and denominator don't share any common factors other than 1?
A: If the GCD is 1, the fraction is already in its simplest form.
-
Q: Are there other ways to simplify fractions besides prime factorization?
A: Yes, the Euclidean algorithm is another efficient method for finding the GCD.
-
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also improves the clarity and efficiency of mathematical expressions.
Conclusion: The Significance of 50/2500 and Beyond
The seemingly simple fraction 50/2500 offers a valuable opportunity to explore fundamental concepts in mathematics, particularly fraction simplification. Understanding how to simplify this fraction, convert it to a decimal and percentage, and apply it to real-world situations highlights the practical relevance of these mathematical skills. This process reinforces the importance of understanding factors, multiples, the GCD, and the concept of equivalent fractions. By mastering these concepts, you'll build a stronger foundation in mathematics, making it easier to tackle more complex problems and applications in various fields. Remember that the ability to simplify and interpret fractions isn't just a mathematical skill; it’s a crucial tool for problem-solving and critical thinking in numerous aspects of life.
Latest Posts
Latest Posts
-
Court Of Hearts
Sep 24, 2025
-
Sequence Of Development
Sep 24, 2025
-
46 4kg In Stone
Sep 24, 2025
-
5 8 Percentage
Sep 24, 2025
-
102f In C
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 50 Of 2500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.