5.6 Of 132
interactiveleap
Sep 21, 2025 · 5 min read
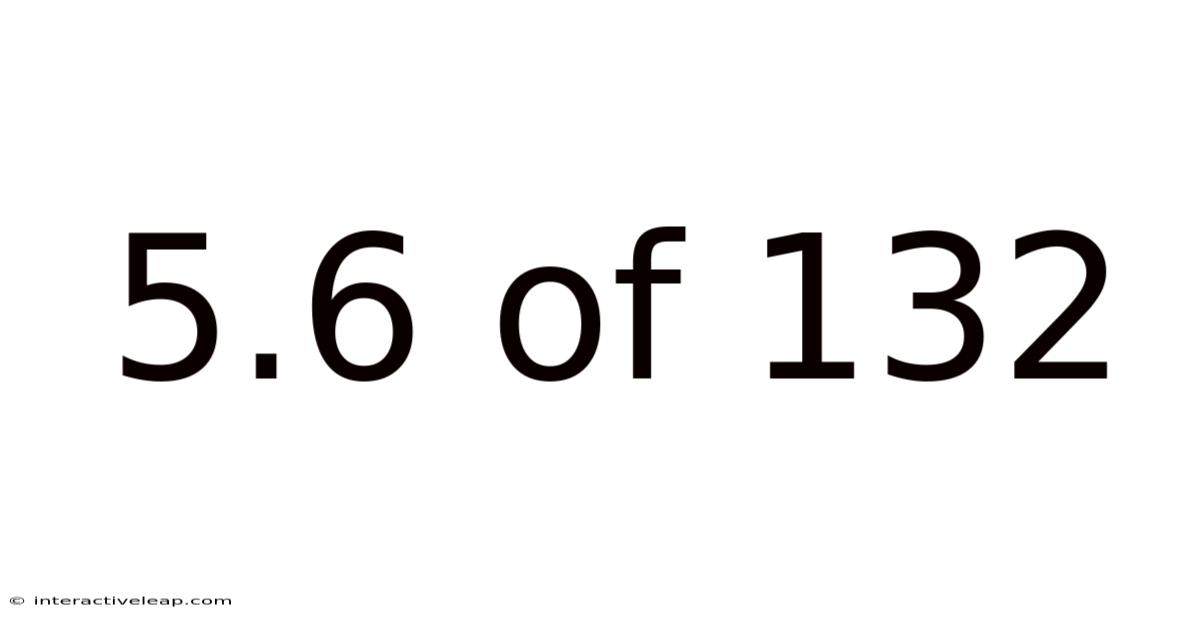
Table of Contents
Decoding 5.6 of 132: Understanding Proportions, Ratios, and Percentages
The seemingly simple phrase "5.6 of 132" presents a common mathematical challenge: understanding proportions and representing them in different formats. This article will delve into the intricacies of this specific example, explaining how to interpret it, calculate related values, and apply these concepts in various real-world scenarios. We'll cover everything from basic calculations to more advanced applications, ensuring a comprehensive understanding for learners of all levels. Understanding these concepts is crucial for various fields, from finance and statistics to everyday problem-solving.
Introduction: What Does "5.6 of 132" Mean?
At its core, "5.6 of 132" represents a part-to-whole relationship. It indicates that 5.6 is a portion of a larger whole, 132. To grasp the full meaning, we need to express this relationship in more meaningful ways, such as percentages, ratios, and fractions. This understanding is vital in numerous applications, such as calculating percentages in sales, determining proportions in recipes, or analyzing statistical data.
Calculating the Percentage
The most common way to represent "5.6 of 132" is as a percentage. A percentage indicates the proportion of a part to the whole, expressed as a fraction of 100. The calculation is straightforward:
(Part / Whole) * 100% = Percentage
In our case:
(5.6 / 132) * 100% ≈ 4.24%
Therefore, 5.6 represents approximately 4.24% of 132. This percentage gives us a clear and concise representation of the relative size of 5.6 compared to 132.
Representing as a Ratio
A ratio expresses the relationship between two quantities. The ratio of 5.6 to 132 can be written as:
5.6 : 132
This ratio can be simplified by dividing both numbers by their greatest common divisor (GCD). Since 5.6 and 132 are not easily simplified to whole numbers, we can leave the ratio as it is or express it as a decimal ratio: approximately 0.0424 : 1. This simplifies the comparison, highlighting that for every 1 unit of the whole, there are approximately 0.0424 units of the part.
Expressing as a Fraction
We can also represent "5.6 of 132" as a fraction:
5.6 / 132
To simplify this fraction, we can multiply both the numerator and denominator by 10 to remove the decimal:
56 / 1320
Now, we can simplify this fraction by finding the greatest common divisor (GCD) of 56 and 1320. The GCD is 8. Dividing both the numerator and the denominator by 8, we get:
7 / 165
This fraction, 7/165, represents the simplest form of the fractional relationship between 5.6 and 132. It provides a clear and concise representation of the proportion.
Real-World Applications: Illustrative Examples
The concept of "5.6 of 132" and its various representations has far-reaching applications across various fields. Let’s explore some illustrative examples:
-
Sales and Marketing: Imagine a company that set a sales target of 132 units. If they sold 5.6 units, the percentage (4.24%) indicates their performance against the target. This information is vital for performance analysis and future planning.
-
Finance: Consider a portfolio with a total value of 132,000 dollars. If 5,600 dollars represents the investment in a particular stock, the ratio and percentage help determine the allocation of assets within the portfolio.
-
Statistics: In statistical analysis, understanding proportions and percentages is fundamental. For instance, if 132 people participated in a survey and 5.6 expressed a particular opinion, the percentage reveals the prevalence of that opinion within the sample.
-
Scientific Research: In scientific experiments, analyzing proportions is crucial. For instance, if 132 trials were conducted and 5.6 showed a positive result, the percentage indicates the success rate of the experiment.
-
Everyday Life: Even in everyday tasks, proportions are important. If a recipe calls for 132 grams of flour and you only have 5.6 grams, you can calculate the adjusted quantities for other ingredients proportionally.
Further Calculations: Extending the Understanding
Understanding the core relationship of 5.6 to 132 allows us to perform various other calculations. For instance, we can determine:
-
The remaining portion: Subtracting 5.6 from 132 gives us the remaining portion (132 - 5.6 = 126.4). We can then express this remaining portion as a percentage of the whole, a ratio, or a fraction, providing a comprehensive understanding of the distribution.
-
Scaling the values: If we need to scale the problem proportionally, we can maintain the same ratio. For example, if the whole becomes 264 (double the original), the corresponding part would also double (11.2).
Frequently Asked Questions (FAQ)
Q: Why is it important to simplify ratios and fractions?
A: Simplifying ratios and fractions makes them easier to understand and compare. It provides a more concise representation of the relationship between the two quantities.
Q: Can I use a calculator for these calculations?
A: Yes, using a calculator is highly recommended, especially for more complex calculations involving decimals.
Q: What if the numbers were different? Would the process be the same?
A: Yes, the process remains the same regardless of the specific numbers. The core concepts of finding percentages, ratios, and fractions remain consistent.
Conclusion: Mastering Proportions and Ratios
Understanding the relationship between "5.6 of 132" involves more than just a simple calculation. It’s about grasping the concept of proportions, ratios, and percentages and applying them effectively in various contexts. By converting the initial statement into percentages, ratios, and fractions, we gain a comprehensive understanding of the relative size of one quantity compared to another. This knowledge is essential not just for academic pursuits but also for effective problem-solving and decision-making in various aspects of daily life and professional endeavors. Mastering these fundamental concepts empowers you to confidently analyze data, make informed decisions, and tackle quantitative challenges with ease. The ability to interpret and manipulate these numerical relationships is a valuable skill applicable across countless domains.
Latest Posts
Latest Posts
-
2500mm In Inches
Sep 21, 2025
-
80 7kg Into Stone
Sep 21, 2025
-
2 3x 7
Sep 21, 2025
-
Kellogg Briand Pact
Sep 21, 2025
-
Verbal Escalation Continuum
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 5.6 Of 132 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.