5 4x 3
interactiveleap
Sep 19, 2025 · 6 min read
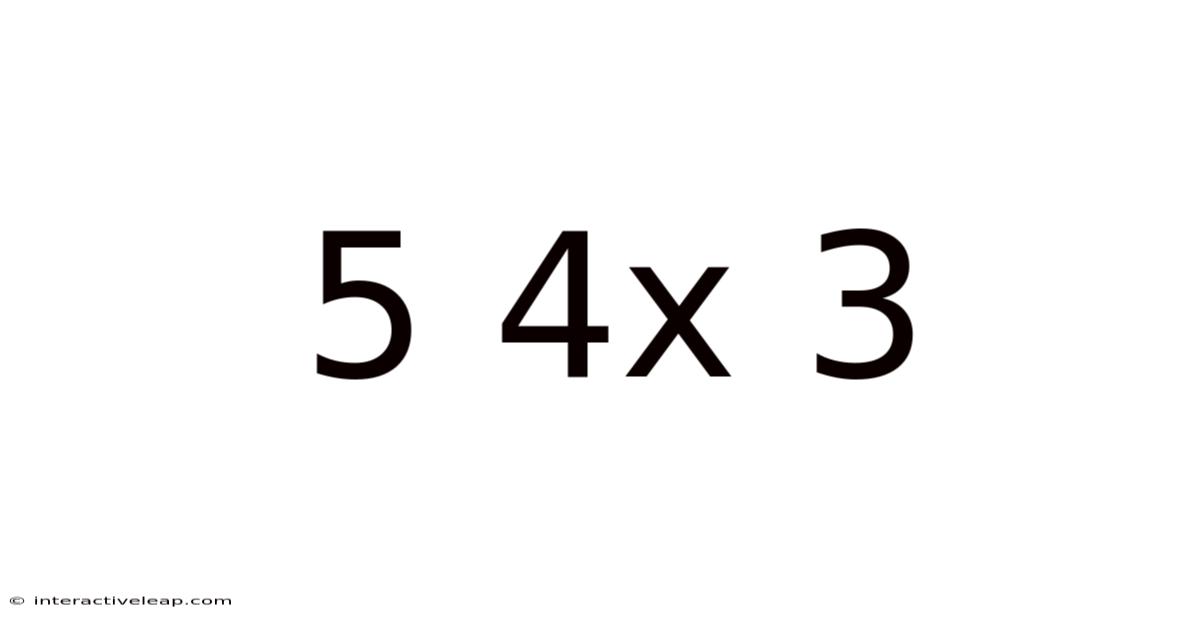
Table of Contents
Decoding 5 x 4 x 3: Exploring Volume, Combinations, and Beyond
This article delves into the seemingly simple mathematical expression "5 x 4 x 3," uncovering its multifaceted applications beyond basic multiplication. We'll explore its relevance in calculating volume, understanding combinations and permutations, and even touch upon its connections to more advanced mathematical concepts. This exploration will be accessible to a broad audience, from elementary school students grasping multiplication to those seeking a deeper understanding of its underlying principles.
Understanding the Basics: Multiplication and its Significance
At its core, "5 x 4 x 3" represents a series of multiplications. It's a concise way of saying: multiply 5 by 4, and then multiply the result by 3. The answer, 60, is the product of these three numbers. While seemingly simple, this operation forms the bedrock of countless calculations across various fields. Multiplication is fundamental to understanding quantities, scaling, and relationships between different variables.
Why is 5 x 4 x 3 important? Its significance extends beyond a simple numerical result. It represents a building block for comprehending more complex mathematical concepts. Let's explore some key applications:
1. Calculating Volume: A Practical Application
One of the most immediate and practical uses of 5 x 4 x 3 is in calculating the volume of a rectangular prism (or cuboid). Imagine a box with dimensions:
- Length: 5 units
- Width: 4 units
- Height: 3 units
The volume of this box is found by multiplying its length, width, and height: 5 x 4 x 3 = 60 cubic units. This calculation is crucial in various fields, including:
- Packaging and logistics: Determining the capacity of boxes for shipping goods.
- Construction and engineering: Calculating the amount of material needed for building structures.
- Manufacturing: Designing containers and molds for products.
Understanding how to calculate volume using multiplication is essential for efficient resource management and problem-solving in numerous real-world scenarios. The seemingly simple 5 x 4 x 3 becomes a powerful tool for practical applications.
2. Combinations and Permutations: Exploring Arrangements
Moving beyond volume calculations, "5 x 4 x 3" also reveals its importance in the realm of combinatorics. Specifically, it represents the number of permutations of selecting 3 items from a set of 5 items without replacement and with order mattering.
Let's illustrate this with an example. Imagine you have 5 different colored balls (red, blue, green, yellow, purple) and you want to arrange 3 of them in a row.
- First choice: You have 5 options for the first ball.
- Second choice: After selecting the first ball, you have 4 remaining options for the second ball.
- Third choice: With two balls already chosen, you have 3 remaining options for the third ball.
Therefore, the total number of possible arrangements (permutations) is 5 x 4 x 3 = 60. This calculation is vital in various fields, including:
- Probability and statistics: Determining the likelihood of specific outcomes in experiments.
- Cryptography: Analyzing the security of encryption methods.
- Computer science: Designing algorithms for sorting and searching data.
The Distinction Between Combinations and Permutations: It's crucial to differentiate between combinations and permutations. In a combination, the order doesn't matter; in a permutation, the order does. In our ball example, if we were only interested in the combination of 3 balls (regardless of order), the calculation would be different (using combinations formula). 5 x 4 x 3 accounts for permutations.
3. Factorials and their Role in Advanced Calculations
The expression "5 x 4 x 3" is closely related to the concept of factorials. A factorial (denoted by !) is the product of all positive integers less than or equal to a given positive integer. For example, 5! (5 factorial) is 5 x 4 x 3 x 2 x 1 = 120.
Notice that 5 x 4 x 3 is a part of 5!. Factorials are fundamental in various advanced mathematical areas, such as:
- Calculus: Used in Taylor series and other expansions.
- Probability and statistics: Calculating probabilities involving permutations and combinations.
- Number theory: Exploring properties of integers and their factorizations.
4. Extending the Concept: Generalizing the Pattern
We can generalize the pattern "5 x 4 x 3" to represent the product of consecutive decreasing integers. This can be written as a partial factorial: n(n-1)(n-2)... where 'n' is the starting integer. Understanding this pattern allows us to extend the concept to larger numbers and more complex scenarios.
5. Beyond the Numbers: Developing Mathematical Thinking
The true power of understanding "5 x 4 x 3" lies not just in the numerical result (60), but in the process of reaching that result. It encourages:
- Logical reasoning: Breaking down a complex problem into smaller, manageable steps.
- Pattern recognition: Identifying recurring mathematical structures and relationships.
- Problem-solving skills: Applying mathematical concepts to solve real-world problems.
These skills are transferable and valuable in many aspects of life, extending far beyond the realm of mathematics.
Frequently Asked Questions (FAQ)
Q: What if the numbers were different?
A: The calculation remains the same – multiply the numbers together sequentially. For instance, 7 x 6 x 5 = 210. The principle of multiplication remains consistent.
Q: Is there a shortcut for this type of calculation?
A: While there isn't a significant shortcut for multiplying three numbers directly, understanding the connection to factorials can provide a more efficient method for larger sequences of decreasing integers.
Q: What if the order of the numbers changes?
A: The order doesn't matter in multiplication. 5 x 4 x 3 is the same as 3 x 5 x 4 or 4 x 3 x 5, the result remains 60. This is the commutative property of multiplication.
Q: Where else can I use this kind of calculation in everyday life?
A: Besides calculating volume, you might use similar calculations for things like determining the number of possible outfits you can create from a selection of clothes, figuring out seating arrangements for a small gathering, or even estimating the number of possible combinations when choosing items from a menu.
Conclusion: The Unsung Power of a Simple Equation
The seemingly simple mathematical expression "5 x 4 x 3" holds far more depth than its initial appearance suggests. From calculating volumes to exploring the intricacies of combinations and permutations, and forming a foundation for understanding factorials and more advanced mathematical concepts, this equation serves as a gateway to a wider understanding of mathematical principles and their practical applications. The real value lies not just in the numerical answer, but in the development of critical thinking, problem-solving skills, and a deeper appreciation for the interconnectedness of mathematical ideas. By understanding this seemingly simple equation, we unlock a broader understanding of the world around us.
Latest Posts
Latest Posts
-
94 6kg In Stones
Sep 19, 2025
-
37 4celsius To Fahrenheit
Sep 19, 2025
-
122lbs In Kg
Sep 19, 2025
-
55lbs To Kg
Sep 19, 2025
-
10 Ounce Steak
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 4x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.