5/16 Of 246
interactiveleap
Sep 15, 2025 · 6 min read
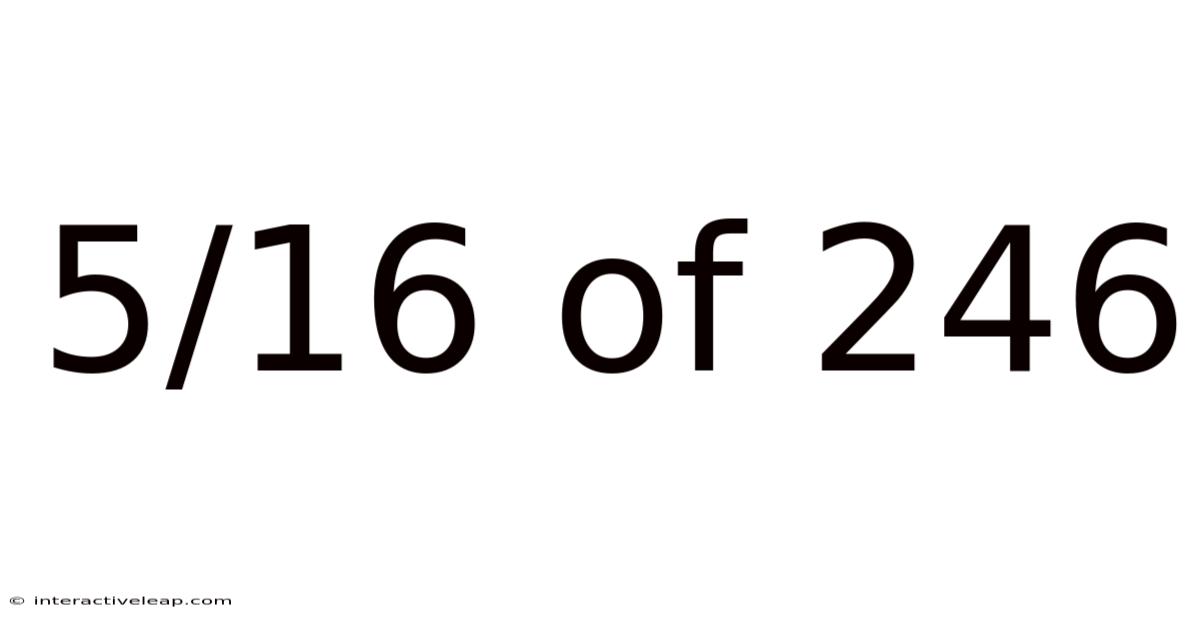
Table of Contents
Decoding 5/16 of 246: A Deep Dive into Fractions and Their Applications
Finding 5/16 of 246 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding the process behind solving this seemingly basic equation unlocks a deeper understanding of fractions, their practical applications, and their importance in various fields. This article will not only show you how to calculate 5/16 of 246 but will also explore the underlying mathematical concepts and real-world scenarios where this type of calculation is crucial. We’ll delve into the mechanics, discuss different solution methods, and address common misconceptions. By the end, you’ll have a comprehensive grasp of this fundamental mathematical operation.
Understanding Fractions: The Building Blocks
Before we tackle 5/16 of 246, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In our problem, 5/16, 5 is the numerator and 16 is the denominator.
Fractions can be:
- Proper fractions: Where the numerator is smaller than the denominator (e.g., 5/16, 1/2, 3/4). These represent values less than 1.
- Improper fractions: Where the numerator is equal to or larger than the denominator (e.g., 16/16, 5/4, 7/3). These represent values equal to or greater than 1.
- Mixed numbers: A combination of a whole number and a proper fraction (e.g., 1 1/2, 2 3/4).
Calculating 5/16 of 246: Step-by-Step Solutions
There are several ways to calculate 5/16 of 246. Let's explore two common methods:
Method 1: Multiplication
This is the most straightforward approach. To find a fraction of a number, we multiply the fraction by the number.
-
Convert the whole number to a fraction: We can express 246 as a fraction by placing it over 1: 246/1.
-
Multiply the fractions: Multiply the numerators together and the denominators together:
(5/16) * (246/1) = (5 * 246) / (16 * 1) = 1230 / 16
-
Simplify the fraction: Now we simplify the resulting fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 1230 and 16 is 2.
1230 / 2 = 615 16 / 2 = 8
Therefore, the simplified fraction is 615/8.
-
Convert to a mixed number (optional): To make the answer easier to understand, we can convert the improper fraction 615/8 into a mixed number. We divide the numerator (615) by the denominator (8):
615 ÷ 8 = 76 with a remainder of 7.
So, 615/8 is equal to 76 7/8.
Therefore, 5/16 of 246 is 76 7/8.
Method 2: Divide and Multiply
This method involves dividing the whole number by the denominator of the fraction and then multiplying the result by the numerator.
-
Divide by the denominator: Divide 246 by 16:
246 ÷ 16 = 15.375
-
Multiply by the numerator: Multiply the result by 5:
15.375 * 5 = 76.875
-
Convert to a fraction (optional): We can convert the decimal 0.875 to a fraction. 0.875 is equivalent to 7/8.
Therefore, 5/16 of 246 is 76 7/8.
Real-World Applications of Fraction Calculations
Understanding how to calculate fractions like 5/16 of 246 is far from being a purely academic exercise. It finds practical application in many everyday situations and professional fields:
- Cooking and Baking: Recipes often require fractional measurements of ingredients. Scaling up or down a recipe necessitates understanding and calculating fractions.
- Construction and Engineering: Precise measurements are vital in construction and engineering. Calculating fractions is crucial for accurate dimensions and material estimations.
- Finance and Accounting: Fractions are used extensively in finance for calculating percentages, interest rates, and proportions of investments.
- Data Analysis and Statistics: In statistics, fractions are fundamental for representing proportions and probabilities in data analysis.
- Manufacturing and Production: Precise measurements and proportions are key in manufacturing processes.
- Software Development: Many algorithms and calculations within computer programs rely on fraction manipulation.
Addressing Common Misconceptions
Several common mistakes can occur when working with fractions. Let's clarify these:
- Incorrect order of operations: Remember to follow the order of operations (PEMDAS/BODMAS). Multiplication and division should be performed before addition and subtraction.
- Improper simplification: Always simplify fractions to their lowest terms by finding the GCD of the numerator and denominator.
- Misunderstanding mixed numbers: Remember to convert mixed numbers to improper fractions before performing calculations, especially multiplication.
- Decimal approximations: While using decimal approximations can be helpful, it's crucial to understand that they can introduce minor inaccuracies, especially when dealing with repeating decimals.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator to perform the multiplication and division involved. However, understanding the underlying mathematical principles is crucial for solving similar problems without relying solely on a calculator.
Q: Why are multiple methods presented?
A: Different methods cater to different learning styles and preferences. Understanding multiple methods provides flexibility and a deeper understanding of the concept.
Q: What if the fraction and the whole number were larger or more complex?
A: The same principles apply. The calculations might become more involved, but the underlying methodology remains the same. You might find using a calculator helpful for larger numbers.
Q: What if the fraction was an improper fraction?
A: Even with improper fractions, the calculation process remains the same. Simply multiply the fractions and then simplify the result.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes the answer easier to understand and work with. It also ensures consistency and avoids unnecessary complexity.
Conclusion: Beyond the Numbers
Finding 5/16 of 246, while seemingly straightforward, opens a window into the broader world of fractions and their significant role in mathematics and numerous real-world applications. Mastering the calculation of fractions is not just about getting the right answer; it's about developing a deeper understanding of mathematical concepts and their practical implications. Through understanding the various methods and addressing common misconceptions, you've gained not only the solution to this specific problem but also a more comprehensive understanding of fractions, empowering you to tackle similar challenges with confidence and accuracy. This knowledge extends far beyond the classroom, proving invaluable in various aspects of daily life and professional endeavors. Remember, the power of mathematics lies not just in the numbers themselves, but in the ability to apply them effectively and creatively.
Latest Posts
Latest Posts
-
11 3km To Miles
Sep 15, 2025
-
8 Sq Meters
Sep 15, 2025
-
The Sleeping Giant
Sep 15, 2025
-
85grams To Oz
Sep 15, 2025
-
Intermittent Fire Alarm
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5/16 Of 246 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.