45 Of 800
interactiveleap
Sep 23, 2025 · 5 min read
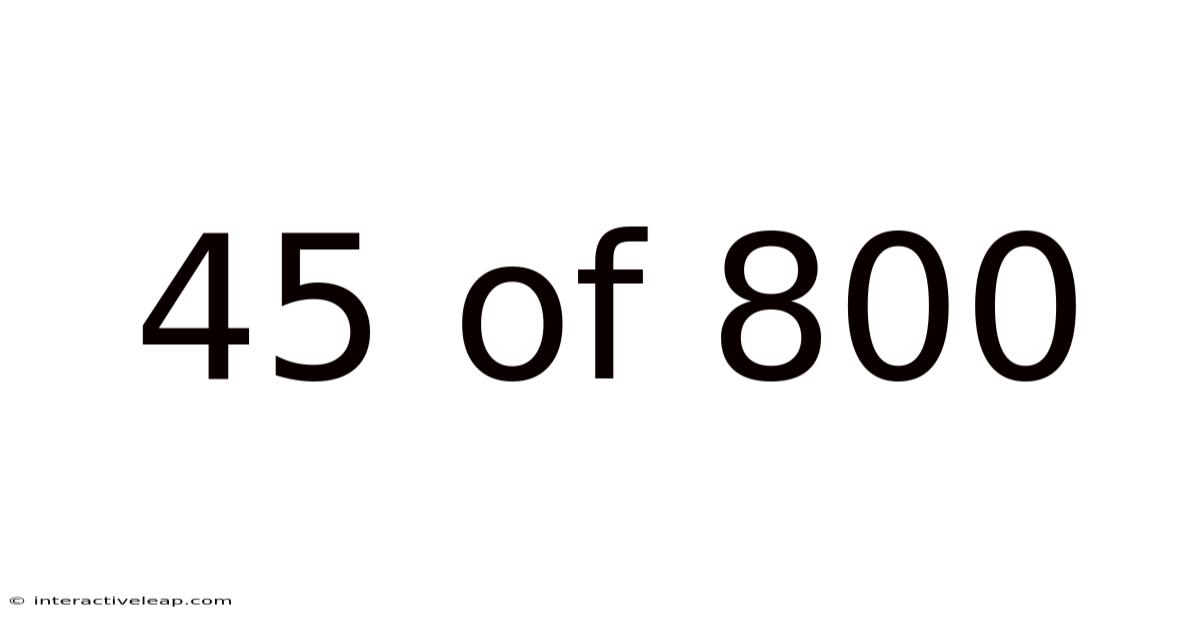
Table of Contents
Decoding the Fraction: Understanding 45/800 and its Implications
The fraction 45/800 might seem insignificant at first glance. Just a simple ratio, right? But understanding how to simplify, interpret, and apply this fraction opens doors to a wider understanding of mathematical concepts, from basic arithmetic to more complex applications in various fields. This article will delve deep into the meaning, simplification, percentage representation, and real-world applications of the fraction 45/800, providing a comprehensive guide for anyone wanting to grasp its significance.
Introduction: Breaking Down 45/800
The fraction 45/800 represents a part-to-whole relationship. It signifies 45 parts out of a total of 800 parts. While seemingly straightforward, this fraction can be simplified, converted to a percentage, and used to solve practical problems across various disciplines. Understanding its implications requires a step-by-step approach, which we'll explore in detail. We'll cover simplifying the fraction, calculating the percentage equivalent, and exploring its significance in scenarios like data analysis, probability, and even everyday decision-making. We’ll also tackle frequently asked questions to ensure a complete understanding of this seemingly simple yet impactful fraction.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve into further analysis, simplifying 45/800 is crucial. This involves finding the greatest common divisor (GCD) of both the numerator (45) and the denominator (800). The GCD is the largest number that divides both 45 and 800 without leaving a remainder. Let's find the GCD using prime factorization:
- Prime factorization of 45: 3 x 3 x 5 = 3² x 5
- Prime factorization of 800: 2 x 2 x 2 x 2 x 2 x 5 x 5 = 2⁵ x 5²
The common factor between 45 and 800 is 5. Therefore, the GCD is 5.
Now, we can simplify the fraction by dividing both the numerator and the denominator by the GCD:
45 ÷ 5 = 9 800 ÷ 5 = 160
Therefore, the simplified fraction is 9/160. This simplified form is easier to work with and provides a clearer representation of the ratio.
Converting to Percentage: Expressing the Fraction as a Proportion
Converting the simplified fraction 9/160 to a percentage allows for easier comparison and interpretation. To convert a fraction to a percentage, we multiply the fraction by 100%:
(9/160) x 100% = 5.625%
Therefore, 45/800 represents 5.625%. This percentage representation provides a readily understandable proportion, making it easier to visualize and communicate the relative size of the fraction.
Real-World Applications: Exploring Practical Uses of 45/800
The fraction 45/800, or its simplified form 9/160, and its percentage equivalent, 5.625%, finds applications in various contexts. Here are some examples:
-
Data Analysis: Imagine a survey of 800 people, where 45 responded positively to a particular question. The fraction 45/800 (or 5.625%) represents the proportion of positive responses. This data can be used to draw conclusions about the population's opinion.
-
Probability: If there are 800 equally likely outcomes in an experiment, and 45 correspond to a specific event, then the probability of that event occurring is 45/800, or 5.625%.
-
Resource Allocation: Consider a budget of $800. If $45 is allocated to a specific project, the fraction 45/800 represents the proportion of the budget allocated to that project.
-
Performance Metrics: In a company with 800 employees, if 45 employees received a specific performance award, 45/800 (or 5.625%) indicates the proportion of employees who received the award. This can be used to assess the company's performance recognition system.
Further Mathematical Explorations:
Beyond its simple application, 45/800 provides a basis for exploring deeper mathematical concepts:
-
Decimals: The fraction 45/800 can be easily converted to a decimal by performing the division: 45 ÷ 800 = 0.05625.
-
Ratios: The fraction represents a ratio of 45 to 800, indicating a proportional relationship between two quantities.
-
Proportions: The fraction can be used to solve proportion problems. For example, if 45 out of 800 items are defective, how many defective items would you expect in a batch of 1000 items? This can be solved using proportional reasoning.
Frequently Asked Questions (FAQ)
-
Q: Can 45/800 be simplified further than 9/160?
- A: No. 9 and 160 share no common factors other than 1, making 9/160 the simplest form of the fraction.
-
Q: What is the reciprocal of 45/800?
- A: The reciprocal is found by flipping the fraction: 800/45. This can be simplified to 160/9.
-
Q: How do I convert 45/800 to a decimal quickly?
- A: Use a calculator to divide 45 by 800. Alternatively, you can use the simplified fraction 9/160 and perform the division.
-
Q: What are some other real-world examples where this fraction might be useful?
- A: This fraction could represent the completion rate of a project (45 tasks completed out of 800 total tasks), the percentage of students who passed an exam, the proportion of a specific product sold compared to the total inventory, etc. The possibilities are vast depending on the context.
Conclusion: The Significance of Understanding Fractions
The seemingly simple fraction 45/800 provides a valuable opportunity to understand fundamental mathematical concepts. Through simplification, percentage conversion, and exploration of real-world applications, we see its practical significance. Understanding fractions like this lays the foundation for tackling more complex mathematical problems and improves analytical skills applicable across diverse fields. The ability to manipulate and interpret fractions is crucial for effective problem-solving in numerous aspects of life, highlighting the importance of mastering this basic yet powerful mathematical tool. By understanding the process of simplification, conversion, and application, we can confidently use 45/800, and other fractions, to analyze data, solve problems, and make informed decisions.
Latest Posts
Latest Posts
-
Centilitre To Litre
Sep 23, 2025
-
Graphic Vector Definition
Sep 23, 2025
-
Purple Pizzazz Brand
Sep 23, 2025
-
Colombia And Coffee
Sep 23, 2025
-
3tbsp To Oz
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 45 Of 800 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.