45 Of 120
interactiveleap
Sep 19, 2025 · 5 min read
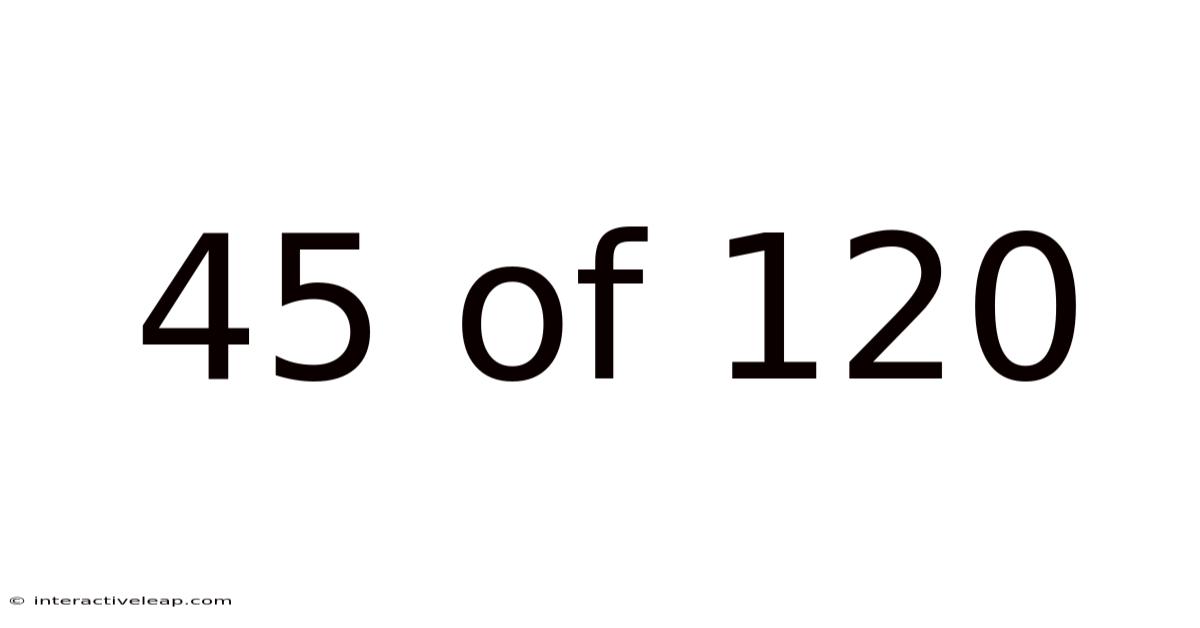
Table of Contents
Decoding the Fraction: Understanding and Applying 45/120
The seemingly simple fraction 45/120 represents a gateway to understanding fundamental mathematical concepts. This article will delve into the intricacies of this fraction, exploring its simplification, decimal representation, percentage equivalent, and practical applications. We'll move beyond mere calculation and explore the broader mathematical principles involved, making this a valuable resource for students and anyone seeking a deeper comprehension of fractions.
Introduction: Why 45/120 Matters
Fractions are a cornerstone of mathematics, appearing in various fields from everyday calculations to advanced scientific applications. Understanding how to manipulate and interpret fractions is crucial for developing strong mathematical reasoning skills. The fraction 45/120, while seemingly straightforward, offers a perfect example to illustrate key concepts like simplification, finding equivalent fractions, and converting between fractions, decimals, and percentages. This article aims to provide a comprehensive guide, empowering you to confidently tackle similar fractional problems.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve into other representations, simplifying the fraction is the first step. This involves finding the greatest common divisor (GCD) of the numerator (45) and the denominator (120). The GCD is the largest number that divides both 45 and 120 without leaving a remainder.
One way to find the GCD is through prime factorization. Let's break down 45 and 120 into their prime factors:
- 45 = 3 x 3 x 5 = 3² x 5
- 120 = 2 x 2 x 2 x 3 x 5 = 2³ x 3 x 5
The common prime factors are 3 and 5. The GCD is the product of these common factors: 3 x 5 = 15.
Now, we divide both the numerator and the denominator by the GCD:
45 ÷ 15 = 3 120 ÷ 15 = 8
Therefore, the simplified fraction is 3/8. This simplified form is crucial because it represents the same value as 45/120 but in a more manageable and easily understandable format.
2. Decimal Representation: Converting Fractions to Decimals
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case, we'll use the simplified fraction 3/8:
3 ÷ 8 = 0.375
Therefore, the decimal representation of 45/120 (or 3/8) is 0.375. This decimal form is useful in various contexts, particularly when performing calculations involving decimals or when comparing fractions to decimal values.
3. Percentage Equivalent: Expressing Fractions as Percentages
Percentages are a common way to represent fractions, often used to express proportions or ratios. To convert a fraction to a percentage, we multiply the decimal equivalent by 100:
0.375 x 100 = 37.5%
Therefore, 45/120 is equivalent to 37.5%. This percentage representation is widely used in various fields, making it a valuable tool for interpreting data and making comparisons.
4. Visual Representation: Understanding Fractions Geometrically
Visualizing fractions can greatly enhance understanding. Imagine a circle divided into 120 equal parts. Shading 45 of those parts represents the fraction 45/120. Simplifying the fraction to 3/8 means we can now visualize this as a circle divided into 8 equal parts, with 3 of them shaded. This visual approach helps to solidify the concept of equivalent fractions and provides a more intuitive grasp of the fraction's magnitude.
5. Applications of 45/120 (or 3/8) in Real-World Scenarios
The fraction 45/120, or its simplified form 3/8, has numerous practical applications:
-
Cooking and Baking: Imagine a recipe that calls for 120 grams of flour, and you only want to make a smaller portion. If you use 45 grams, you're using 3/8 of the original recipe.
-
Measurements: If a project requires a total length of 120 centimeters and you've completed 45 centimeters, you've finished 3/8 of the project.
-
Probability: If there are 120 equally likely outcomes in an experiment, and 45 of them result in a specific event, the probability of that event occurring is 45/120, or 3/8.
-
Data Analysis: If a survey of 120 people shows that 45 prefer a particular product, 3/8 of the respondents prefer that product.
These examples demonstrate that understanding fractions is essential in numerous everyday situations.
6. Further Exploration: Working with More Complex Fractions
While 45/120 is a relatively simple fraction, understanding its manipulation provides a solid foundation for working with more complex fractions. The principles of simplification, decimal conversion, and percentage calculation remain the same, regardless of the size of the numbers involved.
-
Improper Fractions: Fractions where the numerator is larger than the denominator (e.g., 120/45) can be simplified similarly by finding the GCD and then expressed as mixed numbers (a whole number and a fraction).
-
Adding and Subtracting Fractions: To add or subtract fractions, they need to have a common denominator. This involves finding the least common multiple (LCM) of the denominators. After finding the LCM, convert the fractions into equivalent fractions with the LCM as the denominator and then perform the addition or subtraction.
-
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions involves inverting the second fraction and then multiplying.
Mastering these operations is crucial for advanced mathematical applications.
7. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 45/120?
- A: The simplest form is 3/8.
-
Q: How do I convert 45/120 to a decimal?
- A: Divide the numerator (45) by the denominator (120). Or, more efficiently, divide the simplified numerator (3) by the simplified denominator (8), resulting in 0.375.
-
Q: What is the percentage equivalent of 45/120?
- A: 37.5%
-
Q: Can 45/120 be further simplified after simplifying to 3/8?
- A: No, 3/8 is already in its simplest form because 3 and 8 share no common factors other than 1.
8. Conclusion: Mastering Fractions – A Building Block for Success
This in-depth exploration of the fraction 45/120 demonstrates that even seemingly simple fractions offer opportunities to enhance our understanding of fundamental mathematical concepts. By mastering the techniques of simplification, decimal conversion, and percentage calculation, we build a strong foundation for tackling more complex mathematical problems. The ability to confidently manipulate and interpret fractions is invaluable, applicable across various academic and real-world scenarios. Remember to practice regularly to solidify your understanding and build your confidence in handling fractions. The journey towards mathematical proficiency is built upon a solid understanding of these fundamental building blocks. Through consistent practice and application, you'll find that fractions become less daunting and more readily manageable tools in your mathematical arsenal.
Latest Posts
Latest Posts
-
102mm In Inches
Sep 19, 2025
-
1 68 To Feet
Sep 19, 2025
-
100 6f To C
Sep 19, 2025
-
Crossword Clue Gloomy
Sep 19, 2025
-
19 3 4
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 45 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.