40 Of 450
interactiveleap
Sep 24, 2025 · 6 min read
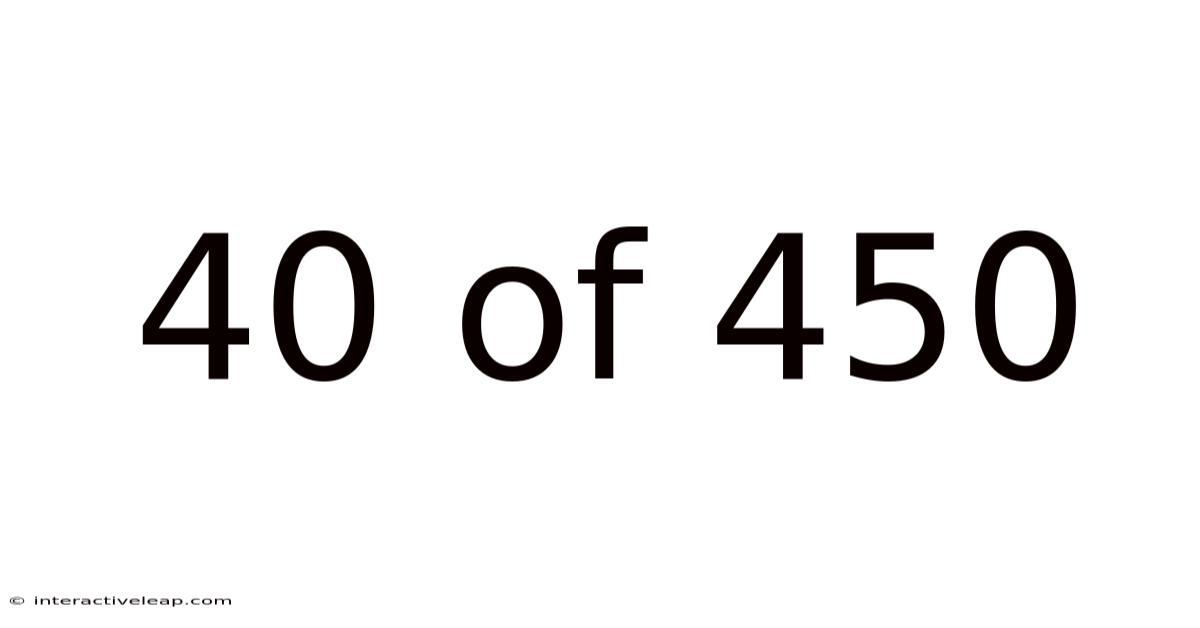
Table of Contents
Decoding 40 out of 450: Understanding Proportions, Percentages, and Applications
The seemingly simple fraction "40 out of 450" holds a wealth of information, representing a proportion, a percentage, and a gateway to understanding various concepts across numerous fields. This article will delve into the meaning of this fraction, exploring its calculation, interpretation, and practical applications in everyday life and specialized areas like statistics and probability. We will also examine how to represent this data effectively and understand its significance within a larger context.
Understanding the Basic Proportion
The phrase "40 out of 450" represents a simple proportion: 40 successful events out of a total of 450 possible events. This can be expressed as a fraction (40/450), a decimal (approximately 0.0889), or a percentage (approximately 8.89%). Understanding these different representations is crucial for interpreting the data and making informed decisions.
Calculating the Percentage
To convert the fraction 40/450 into a percentage, we perform the following calculation:
(40/450) * 100% = 8.89% (approximately)
This calculation shows that 40 represents approximately 8.89% of 450. The approximation arises because the exact decimal value is a recurring decimal. For most practical purposes, rounding to two decimal places provides sufficient accuracy.
Interpreting the Results: What Does 8.89% Mean?
The percentage 8.89% provides a concise and readily understandable representation of the proportion. It indicates that for every 100 possible events, approximately 8.89 events are successful. The specific interpretation depends heavily on the context. For instance:
- In a test: If 40 out of 450 students passed a particular exam, it would indicate a relatively low pass rate. Further investigation into the reasons for the low pass rate might be necessary.
- In manufacturing: If 40 out of 450 products were defective, it would indicate a defect rate of approximately 8.89%. This might require adjustments to the manufacturing process to improve quality control.
- In a survey: If 40 out of 450 respondents answered "yes" to a particular question, it would represent a response rate of about 8.89%. This might be considered low or high depending on the nature of the survey and the target population.
The key takeaway is that the meaning of 8.89% is not inherent; its significance is entirely dependent on the context in which it is presented.
Simplifying the Fraction
Before moving on to more advanced applications, it is beneficial to simplify the fraction 40/450. Both the numerator and the denominator are divisible by 10, resulting in 4/45. This simplified fraction provides an equivalent representation but is easier to work with in some calculations. Further simplification is not possible because 4 and 45 share no common factors other than 1.
Applications in Different Fields
The principles illustrated by "40 out of 450" have widespread applications in various fields:
- Statistics: This proportion can be used to calculate confidence intervals, test hypotheses, and estimate population parameters. For example, in sampling, if 40 out of 450 randomly selected individuals exhibit a certain characteristic, we can use statistical methods to estimate the proportion of the entire population possessing that characteristic.
- Probability: The fraction 40/450 can represent the probability of a specific event occurring. If a random selection is made from a group of 450 items, the probability of selecting one of the 40 specific items is 40/450, or 4/45.
- Business and Finance: This proportion might represent market share, conversion rates, or the success rate of a marketing campaign. For example, if 40 out of 450 potential customers made a purchase, the conversion rate would be 8.89%.
- Science and Research: Proportions are frequently used in scientific experiments and studies to analyze data and draw conclusions. For instance, if 40 out of 450 experimental subjects showed a positive response to a new treatment, this data would be crucial in assessing the treatment's effectiveness.
- Everyday Life: We encounter proportions daily, whether it's calculating discounts, determining the percentage of a task completed, or understanding statistics presented in news reports.
Representing Data Effectively
Visual representations of data, such as pie charts, bar graphs, and line graphs, can greatly enhance the understanding and communication of information. In the case of "40 out of 450," a pie chart would visually represent the 8.89% of successful events compared to the remaining 91.11% of unsuccessful events. A bar graph could compare the number of successful events (40) to the number of unsuccessful events (410). The choice of visual representation depends on the specific context and the intended audience.
Further Considerations and Advanced Applications
The simple proportion 40/450 can serve as a foundation for more complex statistical analysis. For example:
- Confidence Intervals: Using statistical methods, we can calculate a confidence interval around the 8.89% estimate, providing a range within which the true population proportion is likely to fall.
- Hypothesis Testing: We can use hypothesis testing to determine if the observed proportion (8.89%) is significantly different from a hypothesized proportion. This could help us evaluate whether a particular intervention or treatment has a significant impact.
- Regression Analysis: If we have additional data related to the 450 events, we could use regression analysis to model the relationship between the success rate and other relevant factors.
Frequently Asked Questions (FAQ)
-
Q: What is the simplified form of 40/450?
- A: The simplified form is 4/45.
-
Q: How do I convert a fraction to a percentage?
- A: Multiply the fraction by 100%. For example, (40/450) * 100% = 8.89%.
-
Q: What are some real-world examples of using proportions?
- A: Calculating discounts, determining the percentage of a completed task, understanding statistics in news reports, analyzing market share, and assessing the success rate of a marketing campaign are all real-world examples.
-
Q: What statistical methods can be used to analyze data based on a proportion like 40/450?
- A: Confidence intervals, hypothesis testing, and regression analysis are some statistical methods that can be used.
-
Q: Is it always necessary to simplify a fraction?
- A: While simplifying a fraction makes it easier to work with in some cases, it's not always strictly necessary, especially if the original fraction is clear and easily understood in the given context.
Conclusion
The seemingly simple statement "40 out of 450" unlocks a wide range of statistical and mathematical concepts. Understanding how to calculate percentages, interpret proportions, and utilize various visual representations are crucial skills applicable in numerous fields. Beyond the basic calculations, the ability to analyze data using more advanced statistical methods allows for deeper insights and informed decision-making across diverse disciplines. This article has explored the fundamental concepts, provided practical examples, and highlighted the significant role of proportions in various aspects of life, underscoring the importance of numerical literacy and data analysis.
Latest Posts
Latest Posts
-
66 3kg In Lbs
Sep 24, 2025
-
Costume Headless Horseman
Sep 24, 2025
-
Cross Dock Warehouse
Sep 24, 2025
-
20 Of 335
Sep 24, 2025
-
Native American Pattern
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.