40 Of 28
interactiveleap
Sep 16, 2025 · 5 min read
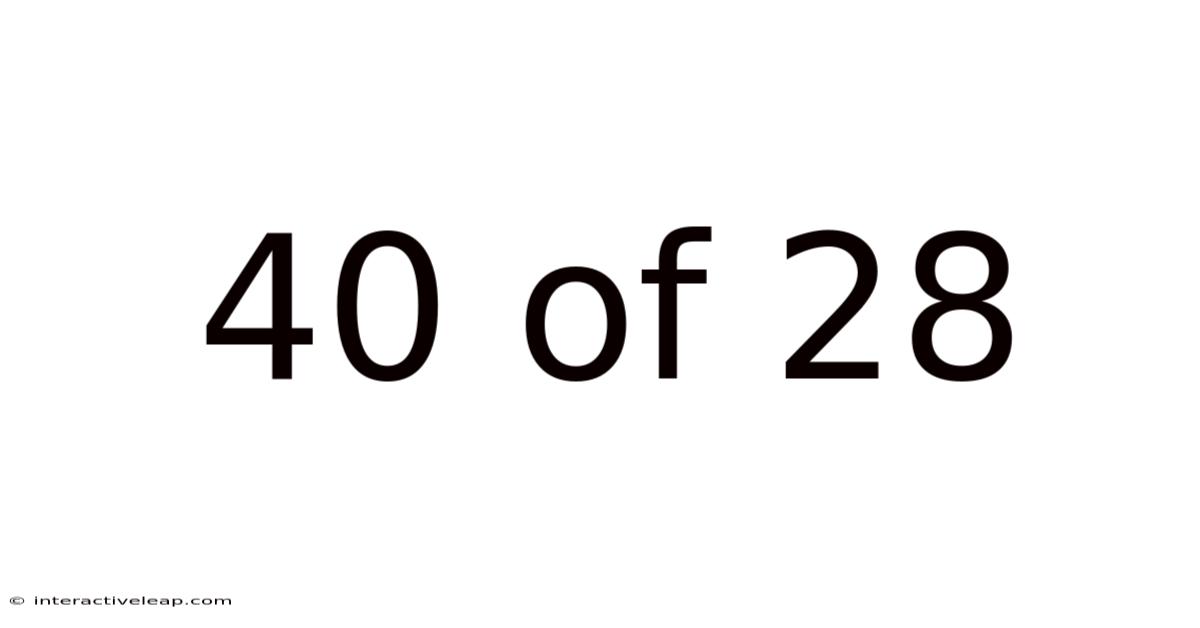
Table of Contents
Decoding the Enigma: Understanding the Fraction 40/28
The seemingly simple fraction 40/28 might appear straightforward at first glance. However, a deeper dive reveals opportunities to explore fundamental mathematical concepts, including simplification, improper fractions, mixed numbers, decimals, and percentages. This comprehensive guide will dissect 40/28, providing a clear understanding for students and anyone looking to refresh their fraction knowledge. We'll explore its various representations and delve into the underlying principles that govern its manipulation.
Introduction: What Does 40/28 Represent?
The fraction 40/28 represents a part of a whole. The number 40 is the numerator, indicating the number of parts we have, while 28 is the denominator, representing the total number of equal parts that make up the whole. This means we have 40 parts out of a possible 28 parts. Since the numerator is larger than the denominator, 40/28 is an improper fraction. Understanding this basic representation is crucial before moving on to more complex manipulations.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before exploring other representations, simplifying the fraction is a crucial first step. This involves finding the greatest common divisor (GCD) of the numerator (40) and the denominator (28). The GCD is the largest number that divides both 40 and 28 without leaving a remainder.
Several methods can be used to find the GCD:
-
Listing Factors: List all the factors of 40 (1, 2, 4, 5, 8, 10, 20, 40) and 28 (1, 2, 4, 7, 14, 28). The largest number present in both lists is 4.
-
Prime Factorization: Break down 40 and 28 into their prime factors:
- 40 = 2 x 2 x 2 x 5 = 2³ x 5
- 28 = 2 x 2 x 7 = 2² x 7 The common prime factors are 2² (or 4). Therefore, the GCD is 4.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. Repeatedly divide the larger number by the smaller number and replace the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
- 40 ÷ 28 = 1 with a remainder of 12
- 28 ÷ 12 = 2 with a remainder of 4
- 12 ÷ 4 = 3 with a remainder of 0 The GCD is 4.
Once we've determined the GCD is 4, we simplify the fraction by dividing both the numerator and the denominator by 4:
40 ÷ 4 = 10 28 ÷ 4 = 7
Therefore, the simplified fraction is 10/7.
2. Converting to a Mixed Number
Since 10/7 is still an improper fraction (the numerator is larger than the denominator), we can convert it to a mixed number. A mixed number combines a whole number and a proper fraction.
To do this, we perform division:
10 ÷ 7 = 1 with a remainder of 3.
This means that 10/7 is equivalent to 1 whole and 3/7. Therefore, the mixed number representation of 40/28 is 1 3/7.
3. Converting to a Decimal
To convert the fraction 10/7 (or 40/28) to a decimal, we simply perform the division:
10 ÷ 7 ≈ 1.42857
Therefore, the decimal representation of 40/28 is approximately 1.42857. Note that this is a repeating decimal, meaning the digits after the decimal point repeat infinitely (in this case, 42857).
4. Converting to a Percentage
To express 40/28 as a percentage, we first convert it to a decimal (as shown above) and then multiply by 100%:
1.42857 x 100% ≈ 142.86%
5. Understanding the Context: Real-World Applications
The fraction 40/28 can represent various real-world situations. For example:
-
Shares: Imagine you own 40 shares of a company, and the total number of shares outstanding is 28. This would represent an ownership stake significantly greater than 100%.
-
Production: A factory produced 40 units of a product, exceeding its planned production of 28 units. The fraction indicates the exceeding production compared to the target.
-
Measurement: Imagine a length of 40 cm compared to a standard length of 28 cm. The fraction would show a length exceeding the standard.
6. Further Exploration: Working with Fractions
Understanding 40/28 provides a stepping stone to mastering more complex fraction operations. Here are some related concepts to explore:
-
Adding and Subtracting Fractions: Requires finding a common denominator.
-
Multiplying Fractions: Multiply numerators and denominators separately.
-
Dividing Fractions: Invert the second fraction and multiply.
-
Working with Negative Fractions: Follow the same rules as positive fractions, considering the sign.
7. Frequently Asked Questions (FAQ)
-
Q: Why is simplifying a fraction important?
- A: Simplifying makes fractions easier to understand and work with. It also ensures consistency in calculations and comparisons.
-
Q: What if I get a different GCD using a different method?
- A: You should always obtain the same GCD regardless of the method used. Double-check your calculations to ensure accuracy.
-
Q: Can all fractions be converted to decimals?
- A: Yes, all fractions can be converted to decimals by performing division. However, some decimals will be terminating (ending) and others will be repeating (non-terminating).
-
Q: What is the significance of the percentage representation?
- A: Percentages provide a convenient way to express fractions as parts of 100, making comparisons and interpretations easier.
8. Conclusion: Mastering Fraction Fundamentals
This in-depth look at 40/28 demonstrates the versatility and importance of understanding fractions. From simplification to decimal and percentage conversion, each step builds upon fundamental mathematical concepts. Mastering these principles is crucial for success in algebra, calculus, and numerous other fields. Remember that practice is key – continue working with different fractions to solidify your understanding. Don't be afraid to explore further mathematical concepts to enhance your skills and confidently tackle more complex problems. The journey of learning mathematics is continuous, and a solid understanding of fractions lays a strong foundation for future achievements. By understanding the underlying principles and practicing different methods, you can approach any fraction with confidence and ease.
Latest Posts
Latest Posts
-
1 7km To Miles
Sep 16, 2025
-
15 Of 48
Sep 16, 2025
-
50 X 20
Sep 16, 2025
-
20 Of 200
Sep 16, 2025
-
Wishes Were Horses
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.