40 Of 24
interactiveleap
Sep 17, 2025 · 6 min read
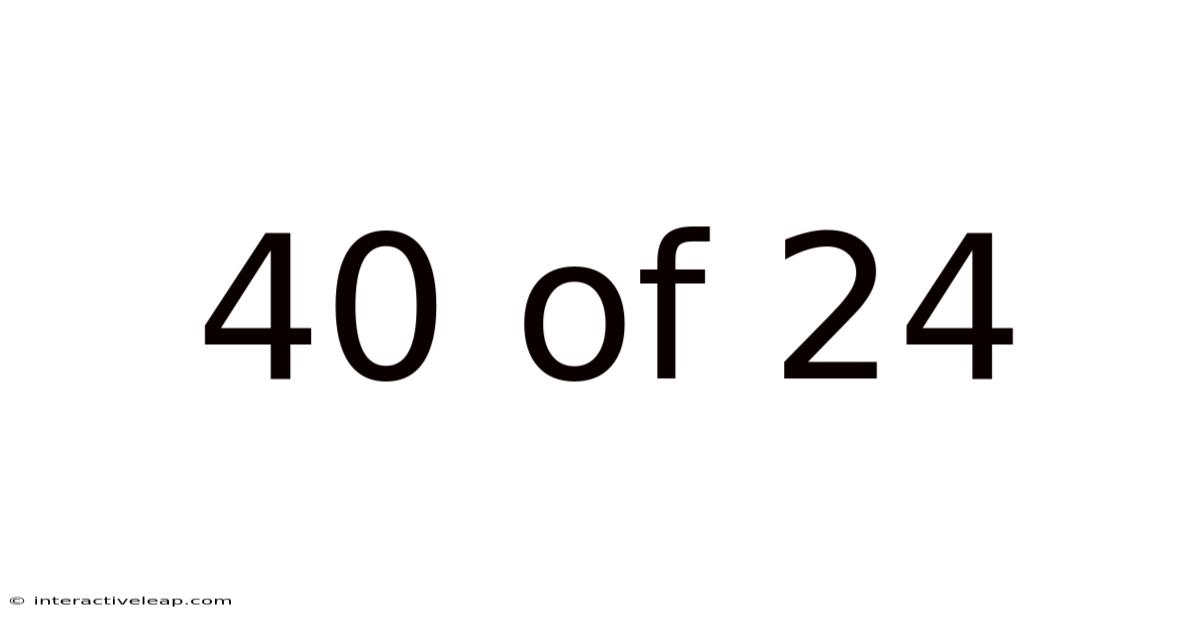
Table of Contents
Decoding the Enigma: Understanding the Fraction 40/24 and its Implications
The seemingly simple fraction 40/24 presents a fascinating opportunity to delve into the world of mathematics, exploring concepts beyond basic arithmetic. This article will unravel the complexities of this fraction, examining its simplification, decimal representation, percentage equivalent, and its applications in various fields. We'll move beyond the simple act of division to understand the underlying principles and broader implications of working with fractions like 40/24. Understanding fractions like this is crucial for mastering fundamental mathematical concepts and applying them to real-world problems.
I. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
The first step in understanding 40/24 is to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (40) and the denominator (24). The GCD is the largest number that divides both numbers without leaving a remainder.
Several methods exist to find the GCD. One common approach is to list the factors of each number:
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Comparing the lists, we see that the largest common factor is 8. Therefore, the GCD of 40 and 24 is 8.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
40 ÷ 8 = 5 24 ÷ 8 = 3
Therefore, the simplified form of 40/24 is 5/3. This simplified fraction is easier to work with and represents the same value as the original fraction.
II. Decimal Representation and Percentage Equivalent
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. In this case:
5 ÷ 3 ≈ 1.666666...
The result is a recurring decimal, meaning the digit 6 repeats infinitely. This is often represented as 1.6̅6̅ or 1.6 recurring.
To express the fraction as a percentage, we multiply the decimal equivalent by 100:
1.666666... × 100 ≈ 166.67%
Therefore, 40/24 is approximately equal to 1.67 as a decimal and 166.67% as a percentage. Note that the percentage exceeds 100% because the fraction is an improper fraction – the numerator is larger than the denominator.
III. Applications of the Fraction 5/3 in Real-World Scenarios
The simplified fraction 5/3, or its decimal equivalent 1.67, has numerous applications across various fields. Let's consider a few examples:
-
Recipe Scaling: Imagine a recipe calling for 24 units of an ingredient. If you want to increase the recipe to yield 40 units of the final product, you need to multiply the quantity of each ingredient by 40/24, which simplifies to 5/3. This means you would use 5/3 times the original quantity of each ingredient.
-
Financial Calculations: Suppose you invest a certain amount of money and it increases by 40/24 (or 5/3) of its initial value. This represents a significant increase, indicating a successful investment.
-
Engineering and Construction: Fractions are fundamental in various engineering and construction calculations. Consider a scenario where a certain length needs to be increased by a factor of 40/24. The simplified fraction 5/3 will provide a more manageable and precise calculation.
-
Data Analysis: In statistical analysis and data representation, fractions are often used. For instance, if 40 out of 24 data points meet a specific criterion, this ratio, represented as 40/24 and simplified to 5/3, would be crucial for understanding the data.
IV. Further Exploration: Improper Fractions and Mixed Numbers
The fraction 40/24 is an improper fraction because the numerator (40) is greater than the denominator (24). Improper fractions can be converted to mixed numbers, which combine a whole number and a proper fraction.
To convert 5/3 to a mixed number, we perform the division:
5 ÷ 3 = 1 with a remainder of 2
This means 5/3 can be written as 1 2/3. This signifies one whole unit and two-thirds of another unit. Both 5/3 and 1 2/3 represent the same value, offering different ways of expressing the same quantity.
V. Understanding the Concept of Ratio and Proportion
The fraction 40/24 fundamentally represents a ratio. It shows the relationship between two quantities: 40 and 24. This ratio can be used to solve problems involving proportion.
For example, if we know that 24 units cost $X, and we want to find the cost of 40 units, we can set up a proportion:
24/X = 40/Y
Solving this proportion for Y (the cost of 40 units) will utilize the simplified ratio 5/3 to derive the answer efficiently. This principle is crucial for solving a wide array of practical problems.
VI. Beyond the Basics: Working with Fractions in Advanced Mathematics
While 40/24 may seem like a simple fraction, understanding its simplification, decimal and percentage equivalents, and its application in real-world scenarios provides a strong foundation for tackling more complex mathematical concepts. This includes:
-
Algebra: Fractions are integral to algebraic equations and manipulations. Solving for variables often involves working with fractions.
-
Calculus: Fractions are crucial in differential and integral calculus, especially when dealing with derivatives and integrals.
-
Probability and Statistics: Fractions are essential for expressing probabilities and ratios in statistical analysis.
VII. Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 40/24?
A1: The simplest form of 40/24 is 5/3.
Q2: How do I convert 40/24 to a decimal?
A2: Divide the numerator (40) by the denominator (24). This results in approximately 1.666... or 1.6̅6̅.
Q3: What is the percentage equivalent of 40/24?
A3: The percentage equivalent is approximately 166.67%.
Q4: Can 40/24 be expressed as a mixed number?
A4: Yes, 40/24 simplifies to 5/3, which can be expressed as the mixed number 1 2/3.
Q5: What are some real-world applications of 40/24 or its simplified form?
A5: Applications include scaling recipes, financial calculations, engineering and construction calculations, and data analysis.
VIII. Conclusion: Mastering Fractions – A Foundation for Success
Understanding the fraction 40/24, from its simplification to its various representations and applications, provides valuable insight into the fundamental principles of mathematics. While seemingly a simple concept, mastering fractions is a cornerstone for success in more advanced mathematical fields and numerous real-world applications. The ability to simplify, convert, and apply fractions effectively showcases a crucial skillset for problem-solving and critical thinking. This article serves not only as a guide for understanding 40/24 but also as a springboard for further exploration of the fascinating world of fractions and their importance in various aspects of life.
Latest Posts
Latest Posts
-
70 Of 32
Sep 17, 2025
-
Decimal Of 5 9
Sep 17, 2025
-
Liter Water Weight
Sep 17, 2025
-
Best Nail Wraps
Sep 17, 2025
-
77 1kg In Stone
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.