40 Of 225
interactiveleap
Sep 17, 2025 · 6 min read
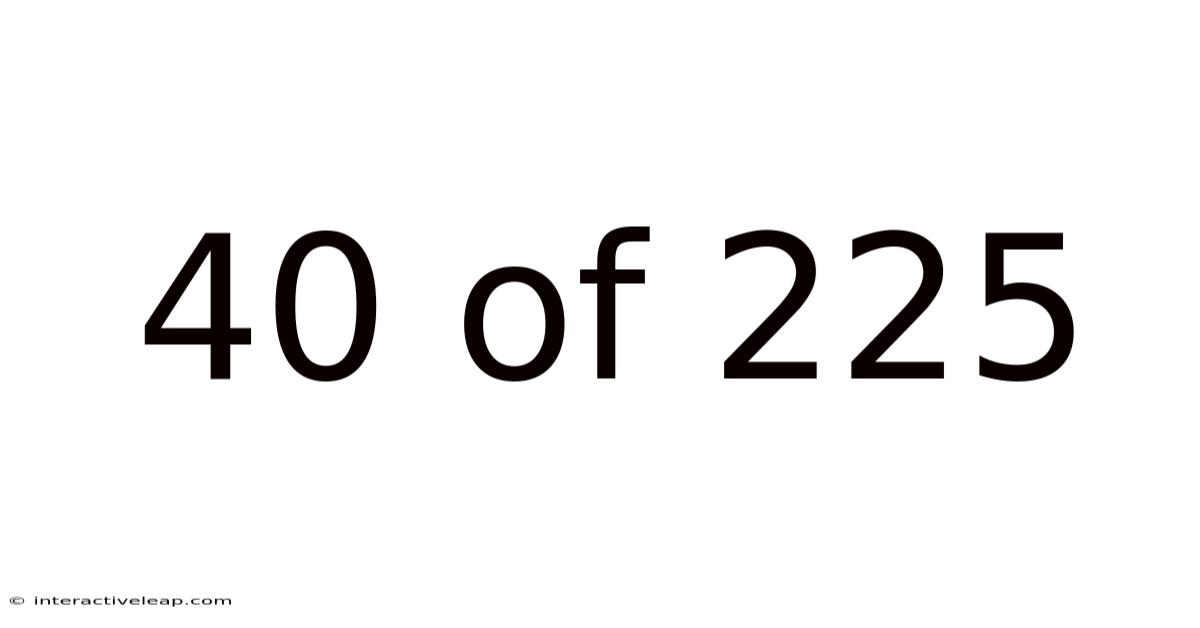
Table of Contents
Understanding the Fraction 40/225: A Comprehensive Guide
The fraction 40/225 might seem intimidating at first glance, but understanding it involves a straightforward process of simplification and interpretation. This article will guide you through the steps of simplifying this fraction, exploring its decimal and percentage equivalents, and examining its applications in various contexts. We'll also delve into the mathematical concepts behind fraction reduction and explore related problems to solidify your understanding. This comprehensive guide aims to equip you with the knowledge and skills to confidently tackle similar fractional problems in the future.
Introduction: Deconstructing 40/225
The fraction 40/225 represents a part-to-whole relationship. The numerator (40) indicates the number of parts we're considering, while the denominator (225) represents the total number of equal parts in the whole. Our primary goal is to simplify this fraction to its lowest terms, making it easier to understand and use in calculations. This process involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. This simplification doesn't change the fraction's value; it simply presents it in a more concise and manageable form. We'll explore this process step-by-step, clarifying the underlying mathematical principles.
Step-by-Step Simplification: Finding the Greatest Common Divisor (GCD)
To simplify 40/225, we need to find the greatest common divisor (GCD) of 40 and 225. Several methods exist for finding the GCD. One common approach is prime factorization:
-
Prime Factorization of 40: We break 40 down into its prime factors. 40 = 2 x 2 x 2 x 5 = 2³ x 5
-
Prime Factorization of 225: We do the same for 225. 225 = 3 x 3 x 5 x 5 = 3² x 5²
-
Identifying Common Factors: Now, we identify the common prime factors between 40 and 225. Both numbers share a single factor of 5.
-
Calculating the GCD: The GCD is the product of the common prime factors raised to the lowest power they appear in either factorization. In this case, the GCD is 5.
-
Simplifying the Fraction: We divide both the numerator and denominator by the GCD (5): 40 ÷ 5 = 8 and 225 ÷ 5 = 45.
Therefore, the simplified form of 40/225 is 8/45.
Alternative Method: Euclidean Algorithm
Another efficient method for finding the GCD is the Euclidean algorithm. This iterative process involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCD.
-
Divide 225 by 40: 225 = 5 x 40 + 25
-
Divide 40 by the remainder (25): 40 = 1 x 25 + 15
-
Divide 25 by the remainder (15): 25 = 1 x 15 + 10
-
Divide 15 by the remainder (10): 15 = 1 x 10 + 5
-
Divide 10 by the remainder (5): 10 = 2 x 5 + 0
The last non-zero remainder is 5, confirming that the GCD of 40 and 225 is 5. We then simplify the fraction as before: 40/225 = 8/45.
Decimal and Percentage Equivalents
Now that we've simplified the fraction to 8/45, we can easily find its decimal and percentage equivalents:
-
Decimal Equivalent: Divide the numerator (8) by the denominator (45): 8 ÷ 45 ≈ 0.1778
-
Percentage Equivalent: Multiply the decimal equivalent by 100: 0.1778 x 100 ≈ 17.78%
Therefore, 40/225 is approximately equal to 0.1778 or 17.78%.
Real-World Applications and Interpretations
The fraction 40/225, or its simplified form 8/45, can represent various real-world scenarios. For example:
-
Test Scores: If a student answered 40 questions correctly out of a total of 225 questions, their score would be 8/45, or approximately 17.78%.
-
Survey Results: If 40 out of 225 respondents chose a particular option in a survey, that option received an 8/45 share of the responses.
-
Proportions: The fraction can represent a proportion, such as 8 parts out of a total of 45 parts.
The interpretation of the fraction depends entirely on the context in which it's used. Understanding the fraction's simplified form (8/45) and its decimal/percentage equivalents (0.1778 or 17.78%) makes it much easier to grasp the implications in any given situation.
Further Exploration: Related Fraction Problems
Let's explore a few related problems to further solidify our understanding of fraction simplification and manipulation.
Problem 1: Simplify the fraction 60/337.5.
First, notice that this fraction involves a decimal number in the denominator. To simplify, we need to convert the decimal to a fraction. 337.5 can be expressed as 3375/10. Therefore, the fraction becomes:
60/(3375/10) = (60 x 10)/3375 = 600/3375
Now, we find the GCD of 600 and 3375 using either prime factorization or the Euclidean algorithm. The GCD is 75. Simplifying:
600/3375 = (600 ÷ 75) / (3375 ÷ 75) = 8/45
Notice that we arrive at the same simplified fraction as before, highlighting the inherent relationships between these numbers.
Problem 2: A recipe calls for 40 grams of sugar for every 225 grams of flour. If you want to use only 100 grams of flour, how much sugar should you use?
This problem involves using proportions. We can set up a proportion using the original fraction:
40/225 = x/100
To solve for x (the amount of sugar needed), cross-multiply:
40 x 100 = 225 x
4000 = 225x
x = 4000/225
Now simplify this fraction (using the GCD of 25):
x = (4000 ÷ 25) / (225 ÷ 25) = 160/9 grams of sugar.
This demonstrates how understanding fractions is crucial for solving real-world problems involving proportions and ratios.
Problem 3: Comparing Fractions
Let's compare 40/225 and another fraction, say 1/5. To compare fractions, we need to have a common denominator.
Convert 1/5 to have a denominator of 45: 1/5 = 9/45
Now we can compare 8/45 and 9/45 directly. Since 8 < 9, we conclude that 8/45 < 9/45, meaning 40/225 < 1/5.
This exercise illustrates the importance of simplifying fractions for easier comparison.
Frequently Asked Questions (FAQ)
-
Q: Why is simplifying fractions important? A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It presents the fraction in its most concise form without changing its value.
-
Q: What if the GCD is 1? A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form.
-
Q: Can I use a calculator to simplify fractions? A: Some calculators have built-in functions to simplify fractions. However, understanding the underlying process of finding the GCD is essential for deeper mathematical comprehension.
-
Q: Are there other methods to find the GCD besides prime factorization and the Euclidean algorithm? A: Yes, there are other methods, but these two are among the most commonly used and efficient.
Conclusion: Mastering Fractions for a Brighter Future
Understanding the fraction 40/225, and more broadly, the concept of fraction simplification, is a fundamental skill in mathematics. By mastering the techniques of finding the GCD and simplifying fractions, you equip yourself with the tools to tackle various mathematical problems with confidence. This knowledge extends beyond the classroom, finding application in countless real-world situations involving proportions, ratios, percentages, and more. The ability to confidently manipulate and interpret fractions is a valuable asset for success in various fields and everyday life. Continue practicing these techniques, exploring related problems, and building your mathematical fluency. With consistent effort, you will gain mastery over this important mathematical concept.
Latest Posts
Latest Posts
-
1 72m In Feet
Sep 17, 2025
-
3 5 Of 240
Sep 17, 2025
-
Magnesium Sulphide Formula
Sep 17, 2025
-
80 Of 55
Sep 17, 2025
-
Parasol Umbrella Black
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 225 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.