40 Divided 8
interactiveleap
Sep 18, 2025 · 5 min read
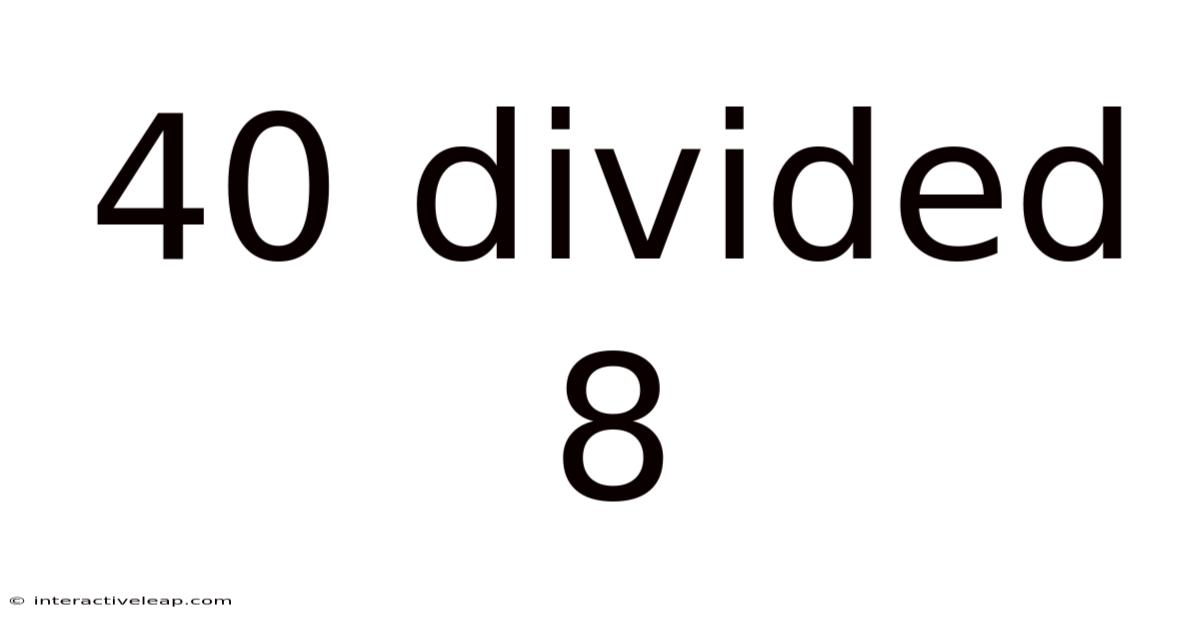
Table of Contents
40 Divided by 8: A Deep Dive into Division and its Applications
Understanding division is a fundamental skill in mathematics, crucial for everyday life and advanced studies alike. This article explores the seemingly simple problem of 40 divided by 8, delving into the process, different methods of solving it, real-world applications, and related mathematical concepts. We'll move beyond simply stating the answer and explore the 'why' behind the calculation, making it accessible and engaging for learners of all levels.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts or groups. The problem "40 divided by 8" asks: "How many times does 8 fit into 40?" The answer to this question forms the basis of many practical calculations and theoretical understandings in mathematics. This exploration will unpack this seemingly simple equation, illuminating the underlying principles and its broader significance.
Methods for Solving 40 ÷ 8
There are several ways to solve 40 divided by 8, each offering a slightly different perspective on the process:
1. Repeated Subtraction:
This is a fundamental approach, especially useful for visualizing division. We repeatedly subtract 8 from 40 until we reach 0.
- 40 - 8 = 32
- 32 - 8 = 24
- 24 - 8 = 16
- 16 - 8 = 8
- 8 - 8 = 0
We subtracted 8 five times, therefore, 40 ÷ 8 = 5.
2. Multiplication Tables:
If you know your multiplication tables, solving 40 ÷ 8 becomes much quicker. You ask yourself: "What number multiplied by 8 equals 40?" The answer, from the 8 times table, is 5. This method highlights the inverse relationship between multiplication and division.
3. Long Division:
Long division is a formal method for dividing larger numbers. While seemingly complex for this particular problem, understanding long division is crucial for tackling more challenging division problems.
5
8 | 40
-40
0
We divide 40 by 8, which goes 5 times. 5 multiplied by 8 is 40. Subtracting 40 from 40 leaves a remainder of 0.
4. Using Visual Aids:
Visual aids can be particularly helpful for younger learners. Imagine you have 40 objects, and you want to arrange them into groups of 8. You would create five groups, each containing 8 objects. This visual representation reinforces the concept of division.
Real-World Applications of Division
Division is used extensively in everyday life, across various disciplines:
-
Sharing Equally: Dividing a pizza among friends, sharing candies among siblings, or splitting the cost of a bill among roommates are common applications of division.
-
Calculating Unit Rates: Determining the price per item (unit price), the speed in miles per hour, or the fuel efficiency in kilometers per liter all involve division. For example, if you travel 40 miles in 8 hours, your speed is 40 ÷ 8 = 5 miles per hour.
-
Scaling Recipes: If a recipe calls for 8 cups of flour and you want to halve the recipe, you would divide the amount of flour by 2 (8 ÷ 2 = 4 cups). Similarly, if you want to double the recipe, you would multiply the amount of flour by 2 (8 x 2 = 16 cups).
-
Averaging: Calculating the average of a set of numbers involves division. Suppose you scored 40 points in 8 games; your average score per game would be 40 ÷ 8 = 5 points.
-
Financial Calculations: Dividing your total income by the number of months in a year helps to determine your average monthly income. Calculating interest rates, profit margins, and unit costs also require division.
-
Engineering and Science: Division is fundamental in numerous scientific and engineering calculations, from determining densities to calculating concentrations and velocities.
Expanding on the Concept: Remainders and Fractions
While 40 ÷ 8 results in a whole number (5), not all division problems result in a neat whole number answer. Sometimes, there's a remainder. For instance, if we divide 43 by 8:
5 R3
8 | 43
-40
3
Here, 8 goes into 43 five times, with a remainder of 3. This remainder can be expressed as a fraction (3/8), leading to the answer 5 3/8. Understanding remainders and fractions is crucial for a complete grasp of division.
Connecting Division to Other Mathematical Concepts
Division is intrinsically linked to other mathematical concepts:
-
Fractions: Division is directly related to fractions. 40 ÷ 8 can be written as the fraction 40/8, which simplifies to 5.
-
Decimals: Division can result in decimal answers. For example, 41 ÷ 8 = 5.125. Understanding decimal representation is essential for working with division problems that don't yield whole numbers.
-
Ratio and Proportion: Division is used to simplify ratios and solve proportions. A ratio of 40:8 can be simplified by dividing both numbers by 8, resulting in the ratio 5:1.
-
Algebra: Division is used extensively in algebra to solve equations and manipulate variables. For example, to solve the equation 8x = 40, we divide both sides by 8 to find x = 5.
Frequently Asked Questions (FAQ)
Q1: What is the inverse operation of division?
A1: The inverse operation of division is multiplication. They are opposite operations that undo each other.
Q2: What happens if you divide by zero?
A2: Dividing by zero is undefined in mathematics. It's not a valid operation because it leads to inconsistencies and contradictions.
Q3: How do I handle division with larger numbers?
A3: For larger numbers, using long division is the most reliable method. This systematic approach ensures accuracy even with complex calculations.
Q4: Are there different types of division?
A4: While the basic concept is consistent, there are different methods of division (as outlined above). Also, there's a distinction between division with whole numbers, fractions, and decimals, each requiring slightly different approaches.
Conclusion: The Significance of Understanding Division
The simple problem of 40 divided by 8 provides a gateway to a deeper understanding of division and its far-reaching applications. From everyday tasks to complex scientific calculations, division plays a vital role. Mastering this fundamental operation is essential for success in mathematics and numerous other fields. This exploration has moved beyond the simple answer of 5, emphasizing the process, different approaches, and the broader mathematical context of division. By grasping these concepts, learners can confidently tackle more challenging problems and appreciate the power and versatility of this fundamental arithmetic operation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 40 Divided 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.