4 X 0.4
interactiveleap
Sep 17, 2025 · 6 min read
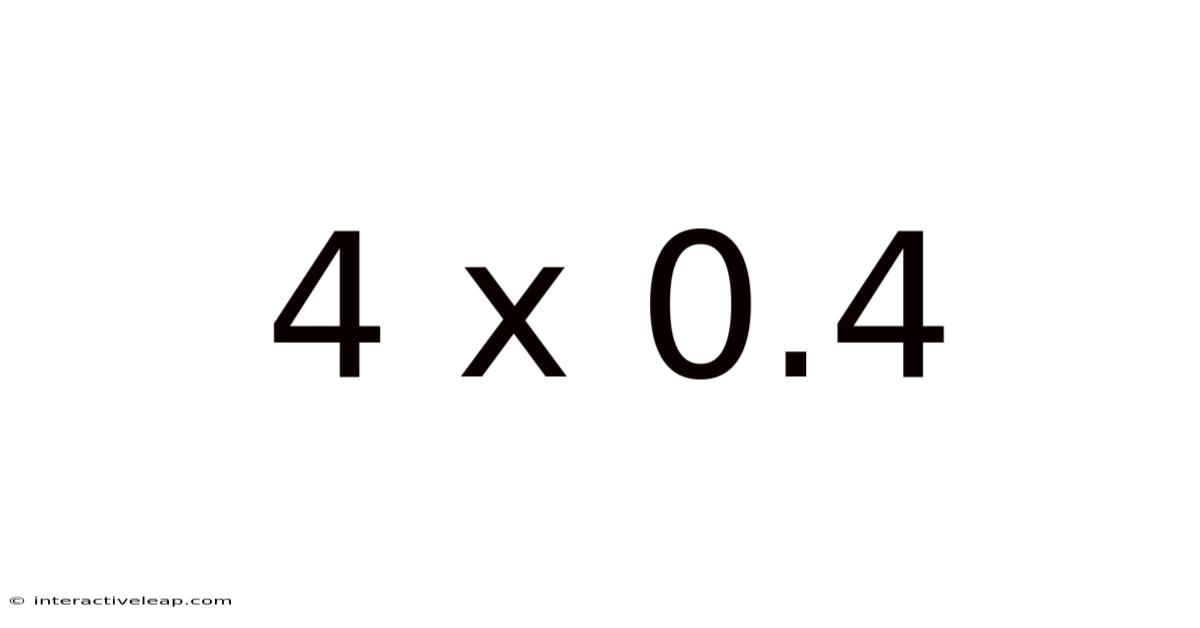
Table of Contents
Unpacking the Seemingly Simple: A Deep Dive into 4 x 0.4
This article explores the seemingly simple mathematical equation, 4 x 0.4, going far beyond the immediate answer. We'll delve into the underlying concepts, explore different methods of solving it, discuss its applications in various fields, and address common misconceptions. Understanding this seemingly basic calculation provides a strong foundation for more complex mathematical operations and real-world problem-solving. This exploration will be suitable for students, educators, and anyone curious about the building blocks of mathematics.
Introduction: More Than Just a Calculation
At first glance, 4 x 0.4 appears trivial. The answer, 1.6, is readily obtainable with a calculator or basic multiplication skills. However, this simple equation offers a rich opportunity to explore fundamental mathematical principles, including decimal multiplication, the commutative property, and real-world applications of multiplication. This deep dive will unveil the layers of understanding hidden within this seemingly straightforward calculation.
Method 1: Direct Multiplication
The most straightforward approach is to perform the multiplication directly. We can treat 0.4 as 4/10, making the equation:
4 x (4/10) = 16/10 = 1.6
This method clearly demonstrates the conversion of a decimal to a fraction, simplifying the multiplication process.
Method 2: Decomposition and Distribution
Another approach involves decomposing 0.4 into its constituent parts. We can express 0.4 as 0.1 + 0.1 + 0.1 + 0.1. This allows us to use the distributive property of multiplication:
4 x (0.1 + 0.1 + 0.1 + 0.1) = (4 x 0.1) + (4 x 0.1) + (4 x 0.1) + (4 x 0.1) = 0.4 + 0.4 + 0.4 + 0.4 = 1.6
This method highlights the distributive property, a fundamental concept in algebra, which states that multiplying a number by a sum is the same as multiplying the number by each addend and then adding the products.
Method 3: Using Fractions
As mentioned earlier, we can represent 0.4 as the fraction 4/10 or its simplified form, 2/5. This leads to:
4 x (2/5) = (4 x 2) / 5 = 8/5 = 1.6
This method reinforces the connection between decimals and fractions, a crucial understanding in mathematics. Converting decimals to fractions often simplifies calculations, particularly when dealing with more complex equations.
Method 4: Visual Representation
Visual aids can significantly aid understanding, particularly for those who benefit from concrete representations. Imagine four groups, each containing 0.4 units. If each unit represents, say, a meter, you could visualize four groups of 0.4 meters each. Combining these lengths gives a total length of 1.6 meters. This approach makes the abstract concept of multiplication more tangible.
Understanding Decimals and Place Value
The equation involves decimals, necessitating a firm grasp of place value. The number 0.4 represents four-tenths (4/10). Understanding place value is crucial for accurately performing decimal operations, avoiding common errors such as misplacing the decimal point. The ability to convert decimals to fractions and vice-versa is an essential skill in mastering decimal arithmetic.
The Commutative Property in Action
The commutative property of multiplication states that the order of the numbers does not affect the product. Therefore, 4 x 0.4 is the same as 0.4 x 4. This property simplifies calculations and allows for flexibility in problem-solving. Understanding this property is vital for more advanced algebraic manipulations.
Real-World Applications: Beyond the Classroom
The simple equation 4 x 0.4 finds numerous applications in everyday life:
- Calculating Costs: If each apple costs $0.40, and you buy four apples, the total cost is 4 x $0.40 = $1.60.
- Measuring Distances: If you take four steps, each 0.4 meters long, your total distance covered is 1.6 meters.
- Calculating Areas: Imagine a rectangle with a length of 4 units and a width of 0.4 units. Its area would be 4 x 0.4 = 1.6 square units.
- Data Analysis: In statistics, this type of calculation might represent a portion of a larger dataset, for example, calculating 40% (0.4) of a sample size of 4.
- Scientific Calculations: In many scientific fields, similar calculations are done regularly to convert units, adjust measurements, and perform basic data analysis.
These examples demonstrate the practical relevance of even the most fundamental mathematical operations. The ability to quickly and accurately perform such calculations is an indispensable life skill.
Addressing Common Misconceptions
Several common misconceptions surround decimal multiplication:
- Misplacing the decimal point: This is a frequent error, often leading to incorrect answers. A thorough understanding of place value is crucial to avoid this.
- Confusing multiplication with addition: Some students might mistakenly add the numbers instead of multiplying them. Clear instruction and practice are vital to prevent this.
- Difficulty visualizing decimals: Abstract concepts like decimals can be challenging for some learners. Visual aids and real-world examples can significantly improve understanding.
Addressing these misconceptions proactively is crucial for ensuring a solid understanding of basic arithmetic.
Expanding the Scope: Beyond 4 x 0.4
While this article focuses on 4 x 0.4, the principles discussed apply broadly to all decimal multiplication problems. Understanding these principles is fundamental to mastering more complex calculations involving decimals, fractions, and algebraic expressions.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to solve 4 x 0.4?
- A: The easiest way is direct multiplication: 4 x 0.4 = 1.6. However, understanding alternative methods is valuable for developing a deeper understanding of mathematical principles.
-
Q: Why is understanding place value important in decimal multiplication?
- A: Place value is crucial for accurately placing the decimal point in the answer. Misplacing the decimal point leads to significant errors.
-
Q: How can I help a child understand decimal multiplication?
- A: Use visual aids like blocks or drawings to represent decimals. Relate the concept to real-world scenarios like money or measurements. Start with simpler examples before progressing to more complex ones. Practice is key.
-
Q: What are some real-world applications of this type of calculation besides the ones mentioned?
- A: Many more applications exist across various fields. For instance, in baking, calculating ingredient amounts often involves decimal multiplication; in finance, calculating interest often relies on these basic calculations. The possibilities are numerous.
Conclusion: The Significance of Simplicity
The seemingly simple equation, 4 x 0.4, provides a rich learning opportunity. By exploring different solution methods and real-world applications, we've revealed the depth of understanding embedded within this fundamental calculation. Mastering this basic operation builds a strong foundation for more advanced mathematical concepts, ultimately equipping individuals with essential problem-solving skills applicable across various fields and life situations. The journey from a simple calculation to a profound understanding underscores the power of mathematical exploration. This exploration highlights that even seemingly basic mathematical concepts offer layers of understanding and applications far beyond the immediate answer. Remember, a solid foundation in basic mathematics is the cornerstone of success in more advanced studies and real-world problem-solving.
Latest Posts
Latest Posts
-
5 4 In Meters
Sep 17, 2025
-
Half Of 240
Sep 17, 2025
-
65 Into Fraction
Sep 17, 2025
-
New York Coordinates
Sep 17, 2025
-
20 Of 57
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 4 X 0.4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.