4 Of 32000
interactiveleap
Sep 25, 2025 · 7 min read
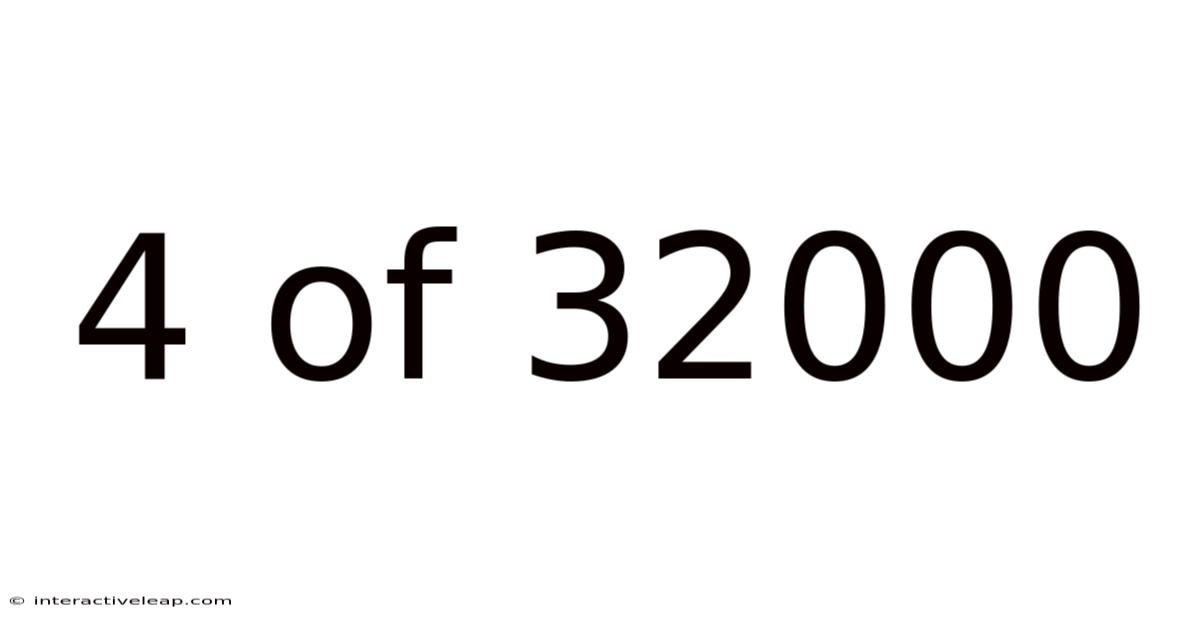
Table of Contents
Decoding the Enigma: Understanding the Significance of 4 out of 32,000
The seemingly simple ratio of 4 out of 32,000, or 4/32000, might initially appear insignificant. However, depending on the context, this fraction can represent a crucial piece of data, whether it's a success rate, a failure rate, or a statistical anomaly. This article delves deep into understanding this ratio, exploring its implications across various fields and illustrating how to interpret its significance. We'll examine methods of calculating probabilities, exploring the concepts of percentages, ratios, and their applications in real-world scenarios. This seemingly small number can hold significant weight, and understanding its meaning can be crucial for informed decision-making.
Understanding the Basic Calculation: Percentages and Ratios
Before jumping into complex applications, let's solidify our understanding of the core concepts. The ratio 4 out of 32,000 essentially means that for every 32,000 instances, an event occurred 4 times. We can represent this in several ways:
- Ratio: 4:32000 (or its simplified form 1:8000)
- Fraction: 4/32000 (simplified to 1/8000)
- Decimal: 0.000125
- Percentage: 0.0125% (or approximately 0.01%)
This simple transformation allows us to visualize the scale of the event relative to the total number of instances. The percentage representation is particularly useful for quick comprehension, showing the event's frequency within the larger context.
Context is King: Interpreting 4/32000 in Different Fields
The meaning of 4/32000 drastically changes depending on the context. Let's explore a few scenarios:
1. Medical Trials: Imagine a clinical trial testing a new drug. 4 out of 32,000 participants experiencing a severe side effect might seem low. However, even a small percentage can be significant if the side effect is life-threatening. Further investigation is necessary to determine if this rate is acceptable given the potential benefits of the drug. A statistical analysis would be needed to determine if this rate is significantly different from the expected background rate of the side effect in the control group.
2. Manufacturing Defects: In a manufacturing plant producing 32,000 widgets, finding 4 defective items represents a 0.0125% defect rate. While seemingly low, this could still be unacceptable depending on the industry standards and the cost of rectifying the defects. This low number might necessitate a review of the manufacturing process to identify and eliminate the source of defects, even if the number seems small.
3. Environmental Studies: If 4 out of 32,000 samples of water from a lake tested positive for a specific pollutant, this relatively low number still signals a potential environmental problem requiring further investigation. The source of the pollutant needs to be identified and addressed to prevent larger-scale contamination. The low number doesn't negate the severity of the issue.
4. Lottery Winnings: Winning the lottery with a probability of 4/32000 implies extremely low odds. While not impossible, the likelihood of winning is incredibly small. This understanding of probability is essential for making informed decisions regarding lottery participation.
5. Scientific Research: In scientific research, observing 4 occurrences out of 32,000 trials might represent a statistically significant result, particularly if it deviates from a null hypothesis. This would depend on the chosen significance level (alpha) and the power of the statistical test conducted. Further statistical analysis is crucial to assess the result's significance.
Beyond Simple Calculation: Delving into Statistical Significance
Simply calculating the percentage or ratio is often insufficient. To truly understand the implications of 4/32000, we must delve into statistical significance. This involves determining if the observed frequency is likely due to chance or represents a genuine effect.
- Null Hypothesis: We typically start with a null hypothesis, which states there's no significant difference or effect. In our example, the null hypothesis could be that the event has a probability of 0%.
- Alternative Hypothesis: The alternative hypothesis proposes that there is a significant difference or effect. This might be that the event has a probability greater than 0%.
- Statistical Tests: Various statistical tests, like chi-squared tests or z-tests, can assess whether the observed data (4 out of 32000) significantly contradicts the null hypothesis. These tests consider the sample size and variability to determine the likelihood of observing such results purely by chance.
- P-Value: The p-value represents the probability of observing the results (or more extreme results) if the null hypothesis were true. A low p-value (typically below 0.05) suggests strong evidence against the null hypothesis, indicating statistical significance.
Expanding the Understanding: Exploring Larger Datasets and Probabilities
The ratio 4/32000 can be viewed within the broader context of probability theory. While it represents a low probability in itself, it's crucial to consider the possibility of this event recurring or escalating. For instance, if the event represents a manufacturing defect, and the rate remains consistently at 4/32000, the cumulative effect over time might lead to a significant number of defective products.
Furthermore, the ratio could be a part of a larger dataset. Perhaps a more comprehensive analysis reveals that the event only occurred in a specific subset of the 32,000 instances. This additional context dramatically changes our interpretation of the significance.
Practical Applications and Real-World Examples
Let's illustrate with a few scenarios:
-
A pharmaceutical company conducts a clinical trial. 4 out of 32,000 participants experience a severe allergic reaction. This is a low percentage, but the severity of the reaction necessitates further investigation to identify risk factors and assess the overall risk-benefit profile of the drug. Is this allergic reaction rate significantly higher than what would be expected in a control group?
-
A quality control team finds 4 defective units out of 32,000 produced. While the defect rate is low, the cost of rectifying these defects needs to be weighed against the potential cost of failing to identify and address the underlying causes. Statistical Process Control (SPC) techniques could be employed to monitor the production process for further improvements.
-
An environmental monitoring agency collects 32,000 water samples and finds 4 contaminated samples. The small number suggests a localized source of contamination, which needs to be identified and remediated to prevent widespread pollution. Further sampling in the vicinity would be crucial to pinpoint the exact source.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage from a ratio like 4/32000?
A: To convert a fraction to a percentage, divide the numerator (4) by the denominator (32000) and then multiply the result by 100%. (4/32000) * 100% = 0.0125%
Q: Is a 0.0125% probability significant?
A: The significance depends entirely on the context. In some scenarios, this probability is considered negligible, while in others, even such a small probability might be cause for concern, especially if the consequences are severe. Statistical tests are needed to determine its significance based on the underlying data and hypothesis.
Q: What statistical tests could I use to analyze data like 4/32000?
A: Depending on the specific context and data, appropriate statistical tests would include chi-squared tests, z-tests, or proportion tests. The choice of test depends on the nature of the data (categorical or continuous) and the specific research question.
Q: How can I determine if a low probability, like 4/32000, is truly rare?
A: Compare it to established base rates or expectations for similar events. If this rate is unexpectedly high or low compared to historical data or theoretical predictions, then it signals a potential deviation that warrants further examination.
Conclusion: Contextual Understanding and Further Analysis are Key
The ratio 4/32000, while seemingly small, carries significant weight depending on the context. A thorough understanding of percentages, ratios, and statistical significance is crucial for correctly interpreting this number. Simple calculation is only the first step. Further analysis, considering the specific application, the potential consequences, and the use of appropriate statistical tests, is vital for making informed decisions based on the data. Remember, context is king, and a seemingly insignificant number can hold crucial insights when analyzed within the correct framework. Always consider the potential implications of the data, both statistically and practically, to reach a meaningful conclusion.
Latest Posts
Latest Posts
-
20 Of 49 99
Sep 25, 2025
-
Lionel First Aid
Sep 25, 2025
-
Tivoli Cinema Cambridge
Sep 25, 2025
-
20 Of 31
Sep 25, 2025
-
Factors For 210
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 4 Of 32000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.