3x 4 2
interactiveleap
Sep 22, 2025 · 6 min read
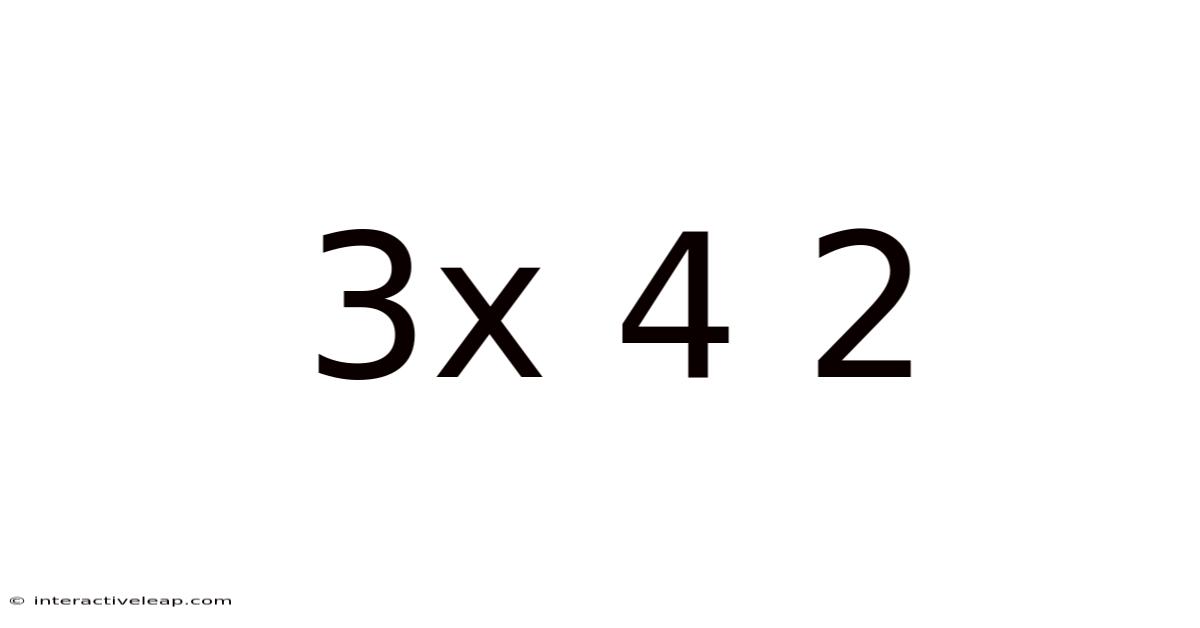
Table of Contents
Decoding the Enigma: A Deep Dive into the Mathematical Concept of 3x4=2 (and Why It's Not True)
The equation "3 x 4 = 2" is, at first glance, baffling. It contradicts fundamental principles of arithmetic learned in elementary school. This article will explore why this equation is incorrect within the standard framework of mathematics, delve into potential misinterpretations that could lead to this erroneous conclusion, and discuss mathematical contexts where similar-looking equations might hold true, albeit with different underlying principles. This exploration will provide a comprehensive understanding of multiplication, its properties, and its limitations, illuminating the core concepts for both beginners and those seeking a deeper appreciation for mathematical logic.
Understanding the Basics of Multiplication
Before we dissect the false equation, let's reaffirm the fundamental concept of multiplication. Multiplication is essentially repeated addition. When we say "3 x 4," we're essentially saying "add 3 four times" or "add 4 three times." Both approaches yield the same result: 3 + 3 + 3 + 3 = 12, and 4 + 4 + 4 = 12. This fundamental principle underpins all multiplication operations within the standard number system. The commutative property of multiplication further clarifies this: the order of the numbers doesn't affect the outcome (3 x 4 = 4 x 3 = 12).
Why 3 x 4 ≠ 2: A Mathematical Refutation
The assertion that 3 x 4 equals 2 directly contradicts the established principles of multiplication. There is no valid mathematical operation or interpretation within the standard number system (integers, rational numbers, real numbers, etc.) that could justify this equation. The result of multiplying 3 by 4 is unequivocally 12. Any attempt to "prove" 3 x 4 = 2 would involve a logical fallacy, a misapplication of mathematical rules, or an operation outside the commonly understood scope of arithmetic.
Potential Sources of Misunderstanding
While 3 x 4 = 2 is demonstrably false, certain scenarios might lead to misunderstandings that could produce this incorrect equation. Let's examine some potential sources of error:
- Typographical errors: A simple typo could lead to misreading the equation. Perhaps the intended equation was 3 x 4 = 12 or a completely different mathematical expression.
- Misinterpretation of symbols: A misunderstanding of the multiplication symbol "x" or the equal sign "=" could lead to an incorrect interpretation.
- Modulo Arithmetic (Clock Arithmetic): Modulo arithmetic, also known as clock arithmetic, operates within a specific range of numbers. For example, in modulo 10 arithmetic, the numbers wrap around after reaching 10. In this system, 12 would be equivalent to 2 (12 mod 10 = 2). However, this doesn't mean 3 x 4 equals 2 in standard arithmetic. It simply implies that the result of 3 x 4 (which is 12) has a remainder of 2 when divided by 10. This is a completely different mathematical operation.
- Incorrect application of mathematical operations: A sequence of operations performed incorrectly could mistakenly lead to an outcome of 2, but this would invalidate the original equation. For example, dividing 12 by 6, then subtracting 10 would incorrectly produce -8. This doesn't make 3 x 4 = 2 valid.
Exploring Modulo Arithmetic in Detail
Modulo arithmetic is a fascinating area of mathematics that provides a different perspective on arithmetic operations. Let's explore this further to clarify its role and its distinction from standard arithmetic.
In modulo arithmetic, we operate within a specific modulus (a positive integer). The result of an operation is the remainder when the result is divided by the modulus.
For example:
-
Modulo 5:
- 3 x 4 = 12. 12 divided by 5 has a remainder of 2. Therefore, in modulo 5 arithmetic, 3 x 4 ≡ 2 (mod 5). The symbol ≡ denotes congruence.
- 7 + 8 = 15. 15 divided by 5 has a remainder of 0. Therefore, 7 + 8 ≡ 0 (mod 5).
-
Modulo 12 (like a clock):
- 3 x 4 = 12. 12 divided by 12 has a remainder of 0. Therefore, 3 x 4 ≡ 0 (mod 12).
It's crucial to understand that this is a different system of arithmetic. While modulo arithmetic uses similar symbols (+, -, x), it operates under different rules, specifically focusing on remainders. It doesn't invalidate standard arithmetic; it simply offers an alternative system with unique applications in various fields, including cryptography and computer science.
Abstract Algebra and Group Theory: A More Advanced Perspective
The concept of 3 x 4 = 2 can also be considered in the abstract algebra context of groups. Groups are sets with a binary operation that satisfies certain properties (closure, associativity, identity element, and inverse element). It's theoretically possible to define a group where a specific operation might yield a result that appears similar to 3 x 4 = 2, but this would involve a completely different definition of the operation 'x' and a different underlying mathematical structure. The operation wouldn't be the standard multiplication we're familiar with.
This highlights that mathematical operations can be defined abstractly and that the familiar operations we use in everyday arithmetic are just one specific instance within a broader framework of mathematical structures.
Frequently Asked Questions (FAQs)
- Q: Is there any mathematical system where 3 x 4 = 2 is true? A: Not in standard arithmetic. However, in modulo arithmetic (specifically modulo 10), the remainder of 3 x 4 when divided by 10 is 2. This is not the same as stating 3 x 4 = 2 directly.
- Q: Could a different definition of multiplication make 3 x 4 = 2 true? A: Theoretically yes, within a completely different mathematical framework, but this would redefine the operation entirely, making it different from standard multiplication.
- Q: Why is it important to understand the limitations of mathematical systems? A: Understanding the limitations helps prevent misinterpretations and ensures the accurate application of mathematical concepts in various contexts.
Conclusion: The Importance of Rigor in Mathematics
The equation "3 x 4 = 2" is fundamentally incorrect within the context of standard arithmetic. While modulo arithmetic and abstract algebra offer alternative perspectives, these systems operate under different rules and do not contradict the validity of standard arithmetic. This exploration emphasizes the importance of rigorous mathematical reasoning, accurate application of rules, and a clear understanding of the underlying principles of each mathematical system. Understanding the nuances of different mathematical structures not only strengthens our grasp of fundamental concepts but also opens doors to more advanced and fascinating areas of mathematical study. The apparent simplicity of the equation belies a deeper lesson about the precision and consistency required in the world of mathematics. It's not just about getting the right answer; it's about understanding why that answer is correct and the implications of diverging from established mathematical principles.
Latest Posts
Latest Posts
-
Millimolar To Micromolar
Sep 22, 2025
-
Whats 3 3
Sep 22, 2025
-
Bunching On Motorway
Sep 22, 2025
-
2 Kg Weight
Sep 22, 2025
-
2 2 1
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3x 4 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.