3x 2 11
interactiveleap
Sep 16, 2025 · 6 min read
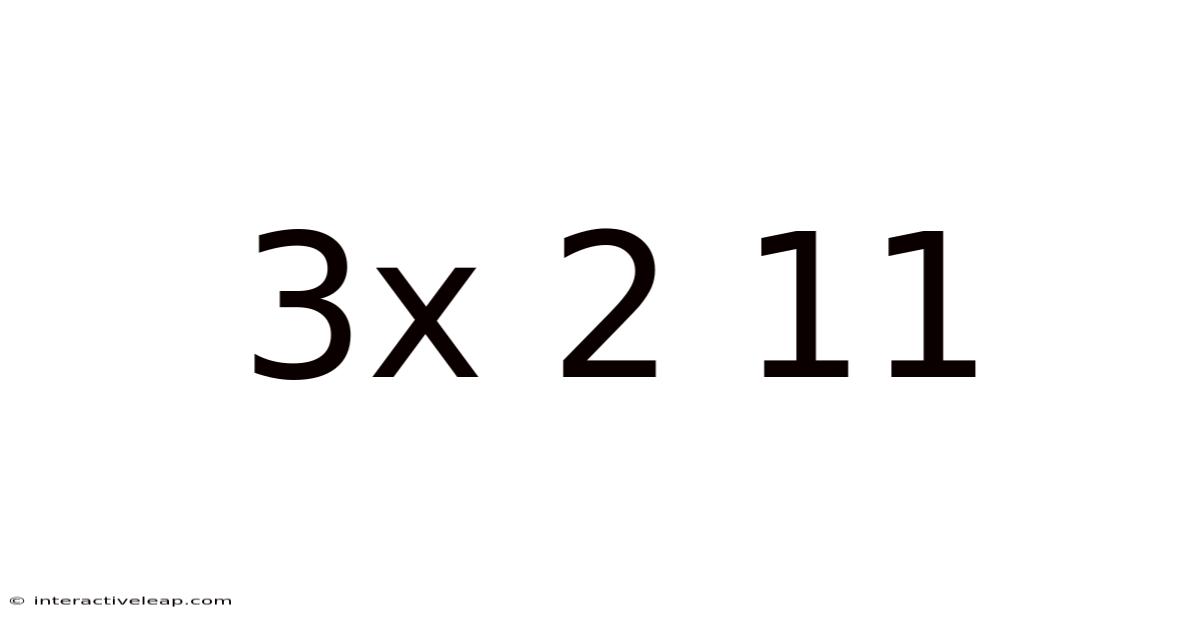
Table of Contents
Decoding the Enigma: A Deep Dive into "3 x 2 = 11"
The seemingly simple equation "3 x 2 = 11" is not, in fact, a true mathematical statement. It's a puzzle, a riddle, a playful challenge to our assumptions about basic arithmetic. This article will explore the various ways this equation can be interpreted, moving beyond the immediate incorrectness to uncover the underlying logic and principles involved. We'll delve into its potential origins, examine possible solutions within different mathematical frameworks, and consider its applications in problem-solving and critical thinking. Understanding "3 x 2 = 11" isn't just about finding the answer; it's about understanding the process of questioning assumptions and exploring alternative perspectives.
I. The Obvious Incorrectness and the Search for Meaning
At first glance, "3 x 2 = 11" is plainly wrong. Basic multiplication dictates that 3 multiplied by 2 equals 6. However, the very existence of this statement suggests that there's more to it than meets the eye. It's a prompt to look beyond the familiar rules of arithmetic and consider unconventional interpretations. This immediately introduces a crucial element of problem-solving: recognizing that a seemingly simple problem might have a hidden complexity requiring a different approach.
II. Possible Interpretations and Solutions
The "3 x 2 = 11" equation challenges us to think outside the box. Let's explore some potential solutions, acknowledging that "correctness" might depend on the context and the rules we establish.
A. Alternate Number Systems:
Our familiar decimal system (base-10) isn't the only one. Other number systems, such as binary (base-2), ternary (base-3), and hexadecimal (base-16), represent numbers differently. Could "3 x 2 = 11" be valid in a different base?
- Base-10 (Decimal): As established, 3 x 2 = 6, not 11.
- Base-2 (Binary): In binary, 3 is represented as 11 and 2 as 10. Their multiplication doesn't yield 11 (binary).
- Base-3 (Ternary): 3 is represented as 10 and 2 as 2. Their product isn't 11 (ternary).
- Higher Bases: Exploring higher bases doesn't immediately lead to a solution where 3 multiplied by 2 results in a value represented as "11" in that base. This highlights that the problem isn't directly solvable using a simple change of base.
B. Logical or Mathematical Operations Beyond Basic Arithmetic:
The equation might involve more complex mathematical operations or logical manipulations hidden within the seemingly simple presentation.
-
Concatenation: Instead of multiplication, perhaps "x" represents concatenation, where numbers are joined together. In this case, 3 concatenated with 2 would result in 32, not 11. This shows that simple concatenation also fails to produce the desired result.
-
Modular Arithmetic: Modular arithmetic involves performing arithmetic within a specified range. For instance, in modulo 5 arithmetic, the result of any calculation is always the remainder after dividing by 5. However, finding a modulo that yields 11 when 3 is multiplied by 2 proves difficult and doesn't seem to directly address the problem's unusual format.
-
Hidden Operations: It's possible that some hidden, unstated operations are involved. Let’s explore some examples to showcase the logic needed to arrive at 11:
- Adding the Digits and Then Multiplying: 3 + 2 = 5. Then, some unknown operation applied to 5 leads to 11. We would need an additional constraint to define this hidden operation.
- Introducing a Constant: We might have a hidden constant, ‘c’, such that 3 x 2 + c = 11. Solving for c, we find c = 5. This suggests an operation that adds 5 to the product of 3 and 2.
C. Redefining the Symbols:
The symbols themselves could have alternative meanings. If we re-interpret the symbols "3", "2", "x", "=", and "11", entirely different possibilities might emerge. However, without a specified context or code, this is entirely speculative and not a concrete mathematical solution.
III. The Importance of Context and Assumptions
The puzzle of "3 x 2 = 11" underscores the importance of clearly defined context and assumptions in problem-solving. In standard mathematics, the equation is incorrect. However, by considering other possibilities—different number systems, additional hidden operations, or redefining symbols—we can construct scenarios where the equation, or something closely resembling it, might hold true. The key takeaway is the need to critically examine assumptions and consider alternative frameworks when facing a seemingly paradoxical situation.
IV. Applications in Problem-Solving and Critical Thinking
The "3 x 2 = 11" puzzle serves as a valuable exercise in problem-solving and critical thinking skills. It demonstrates that:
- Assumptions are Crucial: Our initial assumption of standard arithmetic led to an immediate dismissal of the equation. Challenging this assumption opened the door to exploring alternative solutions.
- Creativity is Key: Finding solutions required creative thinking and considering unconventional interpretations of symbols and operations.
- Multiple Solutions are Possible: There isn’t one single “right” answer. The existence of multiple possible interpretations, even if none perfectly align with the original equation, highlights the flexibility and complexity of mathematical thought.
- Context Matters: The meaning and validity of the equation heavily depend on the defined context and the rules of the system in which it operates.
V. Expanding on the Problem: Introducing Variations
Let's consider variations of the original problem to further explore the underlying concepts:
- Introducing more complex expressions: Instead of just "3 x 2," we could consider more intricate expressions, such as "3 x 2 + 4 - 1 = 11" or "3² + 2 = 11." These variations would require different problem-solving strategies.
- Different symbols: Replace the multiplication symbol "x" with other symbols or operations, perhaps to imply a more intricate function or transformation.
- Working backwards: Start with the result "11" and work backwards to identify potential expressions that could lead to that result. This approach fosters reverse engineering and a deeper understanding of arithmetic operations.
VI. The Puzzle's Potential Origins
The exact origin of the "3 x 2 = 11" puzzle is difficult to trace. However, its simplicity and paradoxical nature suggest it likely emerged as a brain teaser or a playful challenge within mathematical or logical circles. Its viral nature showcases its effectiveness in highlighting the need for careful thinking and consideration of context.
VII. Frequently Asked Questions (FAQ)
-
Is "3 x 2 = 11" mathematically correct? No, in standard arithmetic, 3 multiplied by 2 equals 6, not 11.
-
What are the possible solutions? Possible solutions involve considering different number bases, adding hidden operations (like adding a constant), redefining symbols, or applying more advanced mathematical concepts.
-
Why is this puzzle important? It serves as an excellent exercise in critical thinking, problem-solving, and challenging assumptions. It shows that a seemingly simple problem can have multiple interpretations and solutions depending on the context and the rules applied.
-
What skills does solving this puzzle enhance? Solving this puzzle enhances logical reasoning, analytical skills, creative problem-solving, and the ability to think outside the box.
VIII. Conclusion: Beyond the Numbers
The seemingly simple equation "3 x 2 = 11" is far more than a wrong arithmetic statement. It's a thought-provoking puzzle that challenges our assumptions, encourages creative problem-solving, and highlights the importance of context in mathematical interpretation. By exploring its various potential solutions and their underlying principles, we deepen our understanding not only of arithmetic but also of the broader process of critical thinking and the art of problem-solving. The true value lies not in finding the "correct" answer, but in the journey of exploring possibilities and embracing the inherent ambiguity. The exploration of this deceptively simple statement offers a valuable lesson in the power of questioning, the flexibility of mathematics, and the multifaceted nature of problem-solving itself. The puzzle serves as a constant reminder to always question assumptions and embrace the complexity of seemingly simple statements.
Latest Posts
Latest Posts
-
2 Of 300000
Sep 16, 2025
-
2 25 To Fraction
Sep 16, 2025
-
10 Of 115
Sep 16, 2025
-
Poems Using Alliteration
Sep 16, 2025
-
25 Of 450
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.