38 Of 2350
interactiveleap
Sep 14, 2025 · 5 min read
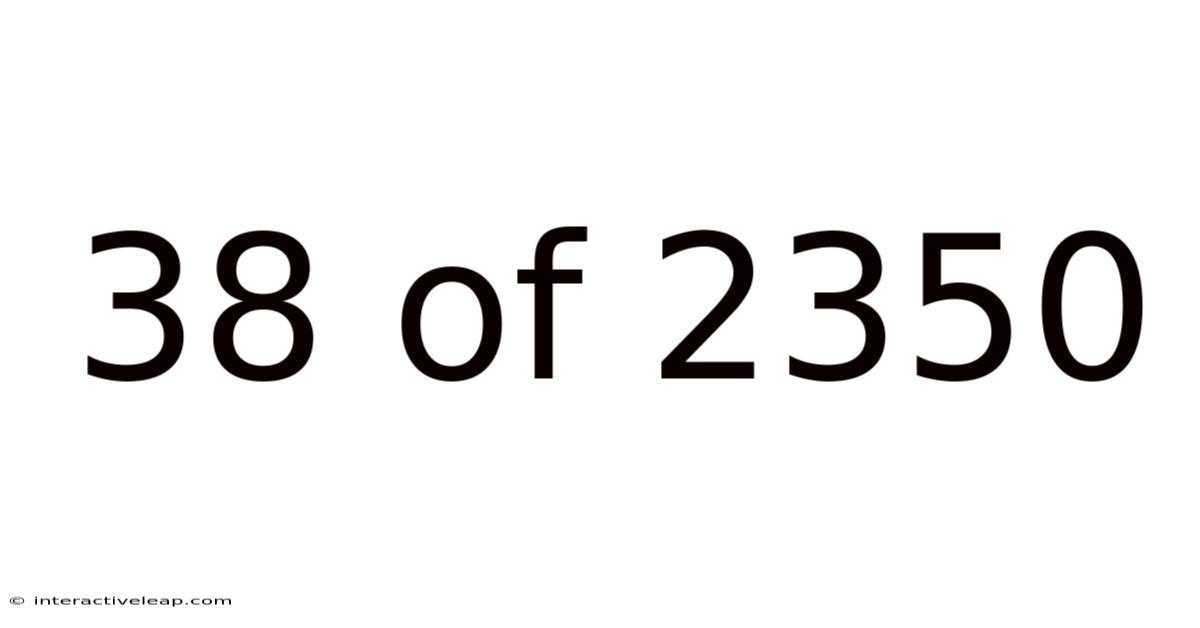
Table of Contents
Understanding the Significance of 38 out of 2350: A Deep Dive into Proportions, Percentages, and Applications
This article explores the meaning and implications of the fraction 38/2350, delving into its proportional representation, percentage calculation, and practical applications across various fields. We'll cover how to interpret this fraction, its relative size, and how to use it effectively in different contexts, from statistical analysis to everyday problem-solving. Understanding this seemingly simple ratio can unlock a deeper understanding of numerical representation and its importance in decision-making.
Introduction: Deconstructing the Fraction 38/2350
The fraction 38/2350 represents a part-to-whole relationship. It indicates that 38 units are present out of a total of 2350 units. This kind of ratio is commonplace in many areas of life, from calculating survey results to determining success rates in manufacturing. Understanding how to express this relationship in different ways – as a decimal, a percentage, or within a broader context – is crucial for drawing meaningful conclusions.
We will begin by simplifying the fraction, calculating the percentage, and then exploring various interpretations and applications. This approach will provide a comprehensive understanding of the numerical significance of 38 out of 2350.
Simplifying the Fraction
Before we dive into percentages and interpretations, let's simplify the fraction 38/2350. Simplifying a fraction means reducing it to its lowest terms by finding the greatest common divisor (GCD) of the numerator (38) and the denominator (2350).
The GCD of 38 and 2350 is 2. Dividing both the numerator and denominator by 2, we get:
38 ÷ 2 = 19 2350 ÷ 2 = 1175
Therefore, the simplified fraction is 19/1175. This simplified form makes it easier to work with and understand the relationship between the parts and the whole.
Calculating the Percentage
Converting the fraction to a percentage provides a more intuitive understanding of its relative size. To calculate the percentage, we divide the numerator by the denominator and multiply the result by 100:
(19 / 1175) * 100 ≈ 1.617%
Therefore, 38 out of 2350 represents approximately 1.617%. This indicates that 38 constitutes a relatively small portion of the total 2350.
Interpreting the Results: Context is Key
The interpretation of 1.617% depends heavily on the context in which this ratio arises. Let's consider some examples:
-
Survey Results: If 38 out of 2350 respondents answered "yes" to a survey question, then 1.617% of respondents agreed. This suggests a relatively low level of agreement. Further investigation might be needed to understand why such a small percentage agreed.
-
Manufacturing Defects: If 38 out of 2350 manufactured items are defective, then the defect rate is approximately 1.617%. This is a low defect rate, suggesting a relatively high level of quality control. However, even a small defect rate can have significant consequences depending on the product and its application.
-
Medical Trials: If 38 out of 2350 patients in a clinical trial experienced a specific side effect, the incidence rate is about 1.617%. This requires careful consideration within the context of the trial's objectives and the severity of the side effect.
Expanding the Understanding: Proportions and Ratios
The fraction 38/2350 can also be expressed as a proportion. A proportion is a statement of equality between two ratios. For instance, we can express the proportion as:
38 : 2350 = x : 100
Solving for x gives us the percentage we calculated earlier (approximately 1.617%). Understanding proportions allows us to scale the ratio up or down to different contexts. For example, we could use this proportion to estimate how many out of 10,000 units would be expected to exhibit the same characteristic.
Applications in Different Fields
The concept of finding a small percentage within a large sample has widespread applications:
- Market Research: Analyzing customer preferences from a large sample size.
- Quality Control: Determining defect rates in manufacturing processes.
- Epidemiology: Tracking the prevalence of diseases within populations.
- Environmental Science: Assessing pollution levels in various locations.
- Finance: Calculating investment returns or risk assessment.
Further Analysis: Statistical Significance
In statistical analysis, the significance of 38 out of 2350 would depend on several factors, including:
- The nature of the data: Is it categorical (yes/no) or continuous?
- The expected proportion: Was there a pre-existing hypothesis about the expected proportion?
- The level of significance: What is the acceptable margin of error?
Statistical tests, such as hypothesis testing, can determine whether the observed proportion (1.617%) is statistically different from an expected or hypothesized proportion. This analysis would help determine whether the observed result is due to chance or represents a genuine effect.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage from a fraction?
A: To calculate the percentage from a fraction, divide the numerator by the denominator and then multiply the result by 100.
Q: What if my fraction is already in its simplest form?
A: If your fraction is already simplified, you can proceed directly to calculating the percentage.
Q: How does the size of the sample affect the interpretation?
A: A larger sample size generally leads to a more reliable estimate. With a larger sample, the results are less likely to be significantly affected by random variation.
Q: What are the limitations of using percentages alone to interpret data?
A: Percentages alone don't provide the entire picture. Contextual information, such as the sample size and the nature of the data, is vital for a complete interpretation. It's also important to consider the potential for bias or confounding factors.
Conclusion: The Power of Proportion
The seemingly simple fraction 38/2350, when examined carefully, offers insights into the broader world of proportions, percentages, and their applications in diverse fields. Understanding how to simplify fractions, calculate percentages, and interpret the results within a specific context is crucial for effective data analysis and decision-making. Remember that the numerical value itself is only a starting point. The real significance lies in how we interpret and apply that value within the context of the problem at hand. Whether it's analyzing survey data, assessing quality control, or interpreting medical trial results, a thorough understanding of proportions and percentages is essential for drawing meaningful conclusions and making informed decisions.
Latest Posts
Latest Posts
-
Latitude Montreal Canada
Sep 14, 2025
-
45km To Miles
Sep 14, 2025
-
North East Landmarks
Sep 14, 2025
-
97lbs To Stone
Sep 14, 2025
-
178kg In Stone
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 38 Of 2350 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.