36 X 7
interactiveleap
Sep 18, 2025 · 6 min read
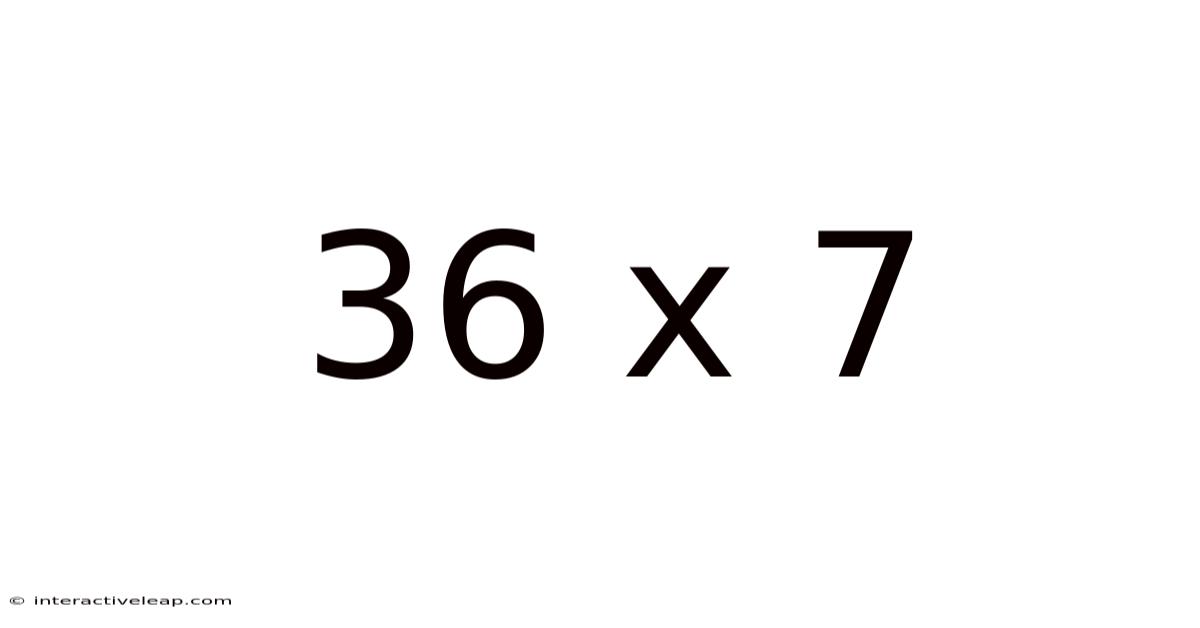
Table of Contents
Unveiling the Wonders of 36 x 7: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem of 36 x 7, delving far beyond the basic answer to uncover the underlying mathematical principles, practical applications, and even the historical context of multiplication itself. We'll journey from basic arithmetic to advanced concepts, making this exploration accessible and engaging for learners of all levels. Understanding 36 x 7 is more than just getting the right answer; it's about appreciating the power and elegance of mathematics.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is simply repeated addition. 36 x 7 means adding 36 seven times: 36 + 36 + 36 + 36 + 36 + 36 + 36. This fundamental understanding forms the bedrock for comprehending more complex multiplication problems. While this method works, it can be time-consuming for larger numbers. That's where more efficient strategies come into play.
Calculating 36 x 7: Different Approaches
Several methods exist to solve 36 x 7 efficiently. Let's explore a few:
1. The Standard Algorithm: This is the method most commonly taught in schools. It involves multiplying the ones digit (6) by 7, then the tens digit (3) by 7, and finally adding the results.
- 6 x 7 = 42. We write down the 2 and carry-over the 4.
- 3 x 7 = 21. We add the carried-over 4 to get 25.
- Therefore, 36 x 7 = 252.
2. Distributive Property: This method leverages the distributive property of multiplication over addition. We can break down 36 into 30 + 6, making the calculation easier:
- (30 + 6) x 7 = (30 x 7) + (6 x 7) = 210 + 42 = 252
3. Mental Math Techniques: With practice, you can develop mental math skills to solve this quickly. For example, you could double 36 to get 72, then double again to get 144, and finally add 72 to get 216. While this specific approach doesn't directly solve 36 x 7, it highlights the flexibility of mental math and the importance of number sense. Approximations can also be helpful; 36 is close to 35 (which is easily multiplied by 7 as 7 x 35 = 245), providing a quick estimate. Then, simply adjust for the difference between 35 and 36.
4. Lattice Multiplication: This visually appealing method is less commonly used today but offers a unique approach. It involves creating a grid and breaking down the numbers. While it might seem more complex initially, it's particularly useful for larger multiplication problems and can be a fun way to learn.
The Importance of Understanding the Process
Regardless of the method used, understanding why the process works is crucial. The standard algorithm, for instance, relies on the place value system of our number system. The distributive property highlights a fundamental algebraic concept. Mastering these underlying principles allows you to tackle more complex problems with confidence.
Beyond the Calculation: Real-World Applications of 36 x 7
While 36 x 7 might seem like an abstract mathematical problem, it has numerous practical applications in everyday life:
- Calculating Costs: Imagine buying 7 items that cost $36 each. Knowing 36 x 7 allows you to quickly calculate the total cost.
- Measuring and Construction: If you're working on a project that requires 7 pieces of wood, each measuring 36 inches long, this calculation helps determine the total length needed.
- Time Management: If a task takes 36 minutes and needs to be repeated 7 times, this calculation determines the total time commitment.
- Data Analysis: In various fields like data science or statistics, the multiplication of numbers plays a role in calculations involving proportions, averages, or other statistical measures.
Exploring the Historical Context of Multiplication
Multiplication, as a mathematical operation, has a rich history. Ancient civilizations, including the Egyptians and Babylonians, developed sophisticated methods of multiplication centuries before the standard algorithms we use today. Understanding this historical context provides a deeper appreciation for the evolution of mathematical thinking and the significance of efficient calculation methods. Early methods often relied on techniques like repeated doubling or using multiplication tables, highlighting the fundamental importance of understanding numerical relationships.
Expanding Our Horizons: Exploring Related Concepts
Understanding 36 x 7 opens doors to exploring related mathematical concepts:
- Factors and Multiples: 36 and 7 are factors of 252. Understanding factors and multiples is crucial in simplifying fractions, solving algebraic equations, and performing other mathematical operations.
- Prime Factorization: Finding the prime factors of 252 helps in simplifying fractions and understanding number properties. 252 = 2 x 2 x 3 x 3 x 7.
- Division: The inverse operation of multiplication is division. Knowing that 36 x 7 = 252 means that 252 / 7 = 36 and 252 / 36 = 7.
- Algebra: Multiplication is a fundamental building block in algebra. Understanding how it works is crucial for solving equations and understanding algebraic expressions.
Frequently Asked Questions (FAQ)
-
Q: What is the quickest way to solve 36 x 7? A: The quickest method depends on your familiarity with different techniques. The standard algorithm, distributive property, or even mental math can be efficient, depending on individual preference and skill level.
-
Q: Are there any tricks to make multiplication easier? A: Yes! Many mental math techniques, such as using the distributive property or breaking down numbers into easier-to-multiply parts, can significantly simplify calculations. Practice and familiarity with various techniques are key.
-
Q: Why is understanding the underlying principles of multiplication important? A: Understanding the underlying principles (like the distributive property and place value) allows for flexibility in problem-solving, enables you to tackle more complex problems, and builds a solid foundation for further mathematical learning.
-
Q: How can I improve my multiplication skills? A: Consistent practice, exploring different methods, and focusing on understanding the underlying principles are crucial. Using flashcards, engaging in interactive math games, and seeking help when needed are also valuable strategies.
Conclusion: The Enduring Power of 36 x 7
This seemingly simple equation, 36 x 7, provides a gateway to exploring a wealth of mathematical concepts and their real-world applications. From the fundamental principles of multiplication to its historical context and its relevance in various fields, this exploration underscores the power and beauty of mathematics. By understanding not just how to solve 36 x 7, but why the methods work, we build a stronger mathematical foundation and cultivate a deeper appreciation for the elegance and practical utility of this essential operation. The journey from a simple calculation to a comprehensive understanding of mathematical principles is a testament to the ever-expanding world of numbers and their enduring influence on our lives. So, next time you encounter 36 x 7, remember the journey, the methods, and the vast mathematical landscape it represents.
Latest Posts
Latest Posts
-
Picogram To Nanogram
Sep 18, 2025
-
216 X 2
Sep 18, 2025
-
40 Divided 8
Sep 18, 2025
-
Square Foot Symbol
Sep 18, 2025
-
Percentage Increase Questions
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 36 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.