36/360 X 40
interactiveleap
Sep 19, 2025 · 6 min read
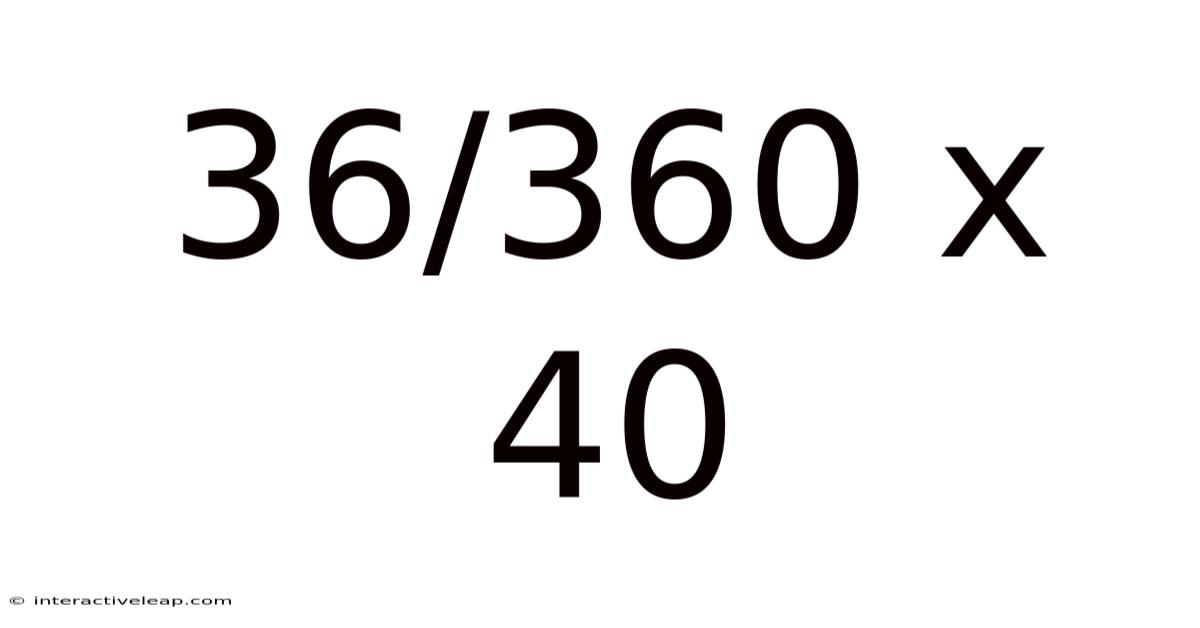
Table of Contents
Decoding 36/360 x 40: A Deep Dive into Fractional Calculations and Real-World Applications
This article explores the seemingly simple calculation, 36/360 x 40, unraveling its mathematical underpinnings and demonstrating its surprising relevance across various fields. We'll move beyond a mere solution to understand the underlying principles of fractions, proportions, and their practical applications in areas like finance, engineering, and everyday life. This detailed explanation will equip you with a deeper understanding of this specific calculation and broader mathematical concepts.
Understanding the Fundamentals: Fractions and Proportions
Before diving into the calculation itself, let's refresh our understanding of fractions and proportions. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts in the whole.
A proportion is a statement that two ratios are equal. For example, 1/2 = 2/4 is a proportion because both ratios represent the same value – one-half. Proportions are crucial in solving many real-world problems where we need to find an unknown quantity based on a known relationship between two or more quantities. The calculation 36/360 x 40 is fundamentally a proportion problem.
Solving 36/360 x 40: A Step-by-Step Approach
The calculation 36/360 x 40 can be approached in several ways. Let's explore two common methods:
Method 1: Simplifying the Fraction First
This method prioritizes simplifying the fraction before performing the multiplication. It often makes the calculation easier and less prone to errors.
-
Simplify the fraction: The fraction 36/360 can be simplified by finding the greatest common divisor (GCD) of 36 and 360. The GCD of 36 and 360 is 36. Dividing both the numerator and the denominator by 36, we get:
36/360 = 1/10
-
Perform the multiplication: Now, we multiply the simplified fraction by 40:
1/10 x 40 = 4
Therefore, 36/360 x 40 = 4.
Method 2: Direct Multiplication and Simplification
This method involves performing the multiplication first and then simplifying the resulting fraction.
-
Perform the multiplication: Multiply the numerator (36) by 40:
36 x 40 = 1440
-
Form the new fraction: This gives us the fraction 1440/360.
-
Simplify the fraction: Now, we simplify 1440/360 by dividing both the numerator and the denominator by their GCD, which is 360:
1440/360 = 4
Again, we arrive at the solution: 36/360 x 40 = 4.
The Significance of the 360-Day Year
The denominator, 360, is often used in financial calculations, particularly when dealing with simple interest. A 360-day year, also known as a banker's year, simplifies calculations compared to a 365-day year (or 366-day leap year). While less accurate, the 360-day year provides a convenient approximation, making computations quicker and easier, especially before the widespread use of calculators and computers. Using a 360-day year is a convention, and its use depends on the specific context and agreement between parties involved.
Real-World Applications: Beyond the Classroom
The calculation 36/360 x 40, despite its seemingly simple nature, finds applications in several real-world scenarios:
-
Simple Interest Calculations: This type of calculation is frequently used in calculating simple interest earned on an investment or loan. The fraction 36/360 might represent the portion of a year (36 days out of a 360-day year), and 40 could represent the principal amount or the daily interest rate.
-
Engineering and Proportionality: Engineers use proportions to scale models, designs, and calculations. The concept underlying 36/360 x 40 – finding a portion of a whole – is fundamental in proportional scaling and similar applications.
-
Percentage Calculations: Expressing 36/360 as a percentage (10%) highlights its application in calculating percentages. For example, finding 10% of 40 is equivalent to 36/360 x 40.
-
Data Analysis and Sampling: In statistical analysis, we frequently work with proportions and samples. Understanding how to manipulate fractions and proportions is essential for accurate interpretation of data.
Explaining the 36/360 Convention in Detail
The use of 360 days in financial calculations is a long-standing convention, rooted in the ease of computation it provides. Here's a deeper look:
-
Simplified Calculations: Dividing by 360 is simpler than dividing by 365 or 366. It's easier to work with multiples of 10, 12, and other easily divisible numbers. This was particularly advantageous before the advent of calculators and computers.
-
Historical Context: The 360-day year has origins in ancient Babylonian mathematics and its use in calendars. While not perfectly reflective of a solar year, its simplicity made it appealing for various calculations.
-
Industry Standard: In many financial institutions and contracts, the 360-day year is still an accepted convention, primarily to ensure consistency and ease of calculation. This convention simplifies calculations of interest, discounts, and other financial instruments.
-
Approximation vs. Accuracy: While less accurate than using the actual number of days in a year, the 360-day year provides a reasonable approximation, particularly for shorter time periods. The error introduced is usually small enough to be acceptable for many applications.
Frequently Asked Questions (FAQ)
Q: Why is the 360-day year used instead of the actual number of days in a year?
A: The 360-day year (banker's year) simplifies calculations, making them easier and quicker, especially for manual computations. This was particularly important before the widespread use of calculators and computers. While less accurate, the approximation is often acceptable for many applications.
Q: Can I use this method for compound interest calculations?
A: No. The 36/360 x 40 calculation is specific to simple interest calculations where the interest is only calculated on the principal amount. Compound interest calculations are more complex and involve different formulas.
Q: Are there any situations where using a 360-day year is inappropriate?
A: Yes. For high-precision calculations or where the exact number of days is crucial (e.g., calculating interest for a very long period), using the actual number of days in a year (365 or 366) is necessary for greater accuracy.
Q: What if the number of days isn't a multiple of 360?
A: The fraction would represent the proportion of the 360-day year. For example, if you had 90 days, the fraction would be 90/360, which simplifies to 1/4.
Conclusion: Mastering Fractions and Their Applications
The seemingly simple calculation 36/360 x 40 offers a window into the world of fractions, proportions, and their wide-ranging applications. Understanding the underlying mathematical principles and their real-world relevance is crucial, not just for academic success, but also for navigating various aspects of life, from personal finance to professional endeavors. While the 360-day year convention offers computational simplicity, always remember to consider the context and the required level of accuracy when making financial or engineering calculations. Mastering these fundamental concepts empowers you to approach complex problems with confidence and precision. Remember, understanding the "why" behind the calculation is as important as knowing the "how."
Latest Posts
Latest Posts
-
170lbs In Stones
Sep 19, 2025
-
Mollie Animal Farm
Sep 19, 2025
-
Define Twilight Years
Sep 19, 2025
-
Athens Greece Democracy
Sep 19, 2025
-
72 To Feet
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 36/360 X 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.