35 Of 240
interactiveleap
Sep 20, 2025 · 5 min read
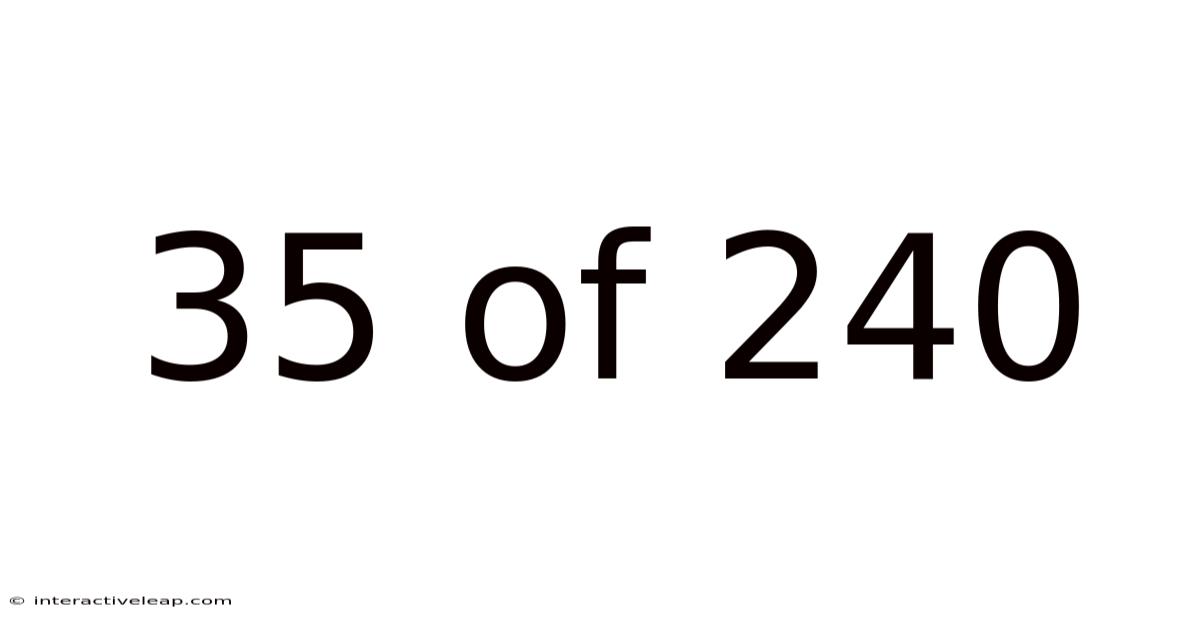
Table of Contents
Decoding the Enigma: Understanding the Fraction 35/240 and its Implications
The seemingly simple fraction 35/240 might appear insignificant at first glance. However, understanding its nuances reveals a wealth of mathematical concepts and practical applications. This article delves deep into the intricacies of this fraction, exploring its simplification, decimal representation, percentage equivalence, and its role in various real-world scenarios. We will also cover common misconceptions and provide clear explanations to solidify your understanding. By the end, you'll not only be able to confidently work with 35/240 but also appreciate the broader mathematical principles it embodies.
Introduction: A Deeper Dive into Fractions
Fractions are fundamental building blocks of mathematics, representing parts of a whole. They consist of a numerator (the top number, 35 in this case) and a denominator (the bottom number, 240). The fraction 35/240 signifies 35 out of 240 equal parts. Understanding fractions is crucial in various fields, including cooking, construction, finance, and even everyday life. This article focuses on 35/240, exploring its properties and applications in detail.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before delving into other aspects, simplifying the fraction is essential. This involves finding the greatest common divisor (GCD) of the numerator (35) and the denominator (240). The GCD is the largest number that divides both 35 and 240 without leaving a remainder.
To find the GCD, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- Prime factorization of 35: 5 x 7
- Prime factorization of 240: 2 x 2 x 2 x 2 x 3 x 5
The only common prime factor is 5. Therefore, the GCD of 35 and 240 is 5.
Now, we simplify the fraction by dividing both the numerator and the denominator by the GCD:
35 ÷ 5 = 7 240 ÷ 5 = 48
Therefore, the simplified fraction is 7/48. This simplified form is easier to work with and represents the same value as 35/240.
Decimal Representation and Percentage Equivalence
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. Let's convert 7/48:
7 ÷ 48 ≈ 0.1458333...
This is a recurring decimal, meaning the digits after the decimal point repeat infinitely. We can round this to a specific number of decimal places depending on the required precision. For example, rounded to three decimal places, it becomes 0.146.
To find the percentage equivalent, we multiply the decimal representation by 100:
0.1458333... x 100 ≈ 14.58%
Therefore, 35/240, or its simplified form 7/48, is approximately equal to 0.146 or 14.58%.
Real-World Applications: Illustrative Examples
The fraction 35/240, or its simplified version 7/48, can be applied in various real-world situations:
-
Surveys and Statistics: Imagine a survey of 240 people, where 35 responded positively to a particular question. The fraction 35/240 represents the proportion of positive responses. Simplifying it to 7/48 makes it easier to understand and visualize the result.
-
Proportions in Recipes: Let's say a recipe calls for 240 grams of flour and 35 grams of sugar. The fraction 35/240 indicates the ratio of sugar to flour in the recipe. Simplifying it shows the reduced ratio of sugar to flour.
-
Financial Calculations: If you have invested $240 and earned a profit of $35, the fraction 35/240 represents your profit margin, which can be simplified and expressed as a percentage.
-
Probability: In a scenario with 240 equally likely outcomes, 35 of which represent a specific event, the fraction 35/240 gives the probability of that event occurring. Again, simplification aids in easier understanding and interpretation.
Mathematical Properties and Further Exploration
Beyond its practical applications, 35/240 offers opportunities to explore broader mathematical concepts:
-
Rational Numbers: Fractions are rational numbers, which can be expressed as the ratio of two integers. This property distinguishes them from irrational numbers like π (pi) or √2 (square root of 2).
-
Equivalence of Fractions: The fraction 35/240 is equivalent to its simplified form 7/48. This highlights the concept that different fractions can represent the same value.
-
Decimal Expansions: The decimal representation of 7/48 exhibits a recurring pattern, providing an example of the properties of rational numbers' decimal expansions.
Addressing Common Misconceptions
-
Improper Fractions vs. Mixed Numbers: While 35/240 is a proper fraction (numerator < denominator), some might mistakenly convert it into a mixed number (a whole number and a proper fraction). While possible, it's often unnecessary for calculations or interpretations unless specifically needed for a particular context.
-
Oversimplification: Some might try to simplify the fraction further beyond its simplest form (7/48). This is incorrect; a fraction is in its simplest form when the numerator and denominator have no common factors other than 1.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 35/240?
-
A: The simplest form is 7/48.
-
Q: What is the decimal equivalent of 35/240?
-
A: Approximately 0.1458333... It's a recurring decimal.
-
Q: What is the percentage equivalent of 35/240?
-
A: Approximately 14.58%.
-
Q: Can 35/240 be expressed as a mixed number?
-
A: Yes, it can be expressed as 0 7/48, but the simplest and most often used form is the proper fraction 7/48.
-
Q: What are some real-world applications of this fraction?
-
A: Many, including surveys, recipes, finance, and probability calculations. See the "Real-World Applications" section for examples.
Conclusion: A Comprehensive Understanding
This article has explored the fraction 35/240 comprehensively, going beyond a simple numerical calculation. We've examined its simplification, decimal and percentage representation, and various practical applications. By understanding the fundamental concepts related to fractions, greatest common divisors, and decimal expansions, you can confidently tackle similar problems and appreciate the deeper mathematical principles involved. Remember, the seemingly simple fraction holds a wealth of knowledge within its seemingly simple structure, highlighting the beauty and power of mathematics in everyday life. The ability to manipulate and interpret fractions is a valuable skill applicable across a wide spectrum of disciplines.
Latest Posts
Latest Posts
-
176 To Feet
Sep 20, 2025
-
Ladder Santa Climbing
Sep 20, 2025
-
125 Divided 2
Sep 20, 2025
-
2 37m In Cm
Sep 20, 2025
-
X 3 64
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 35 Of 240 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.