30 Of 270
interactiveleap
Sep 19, 2025 · 6 min read
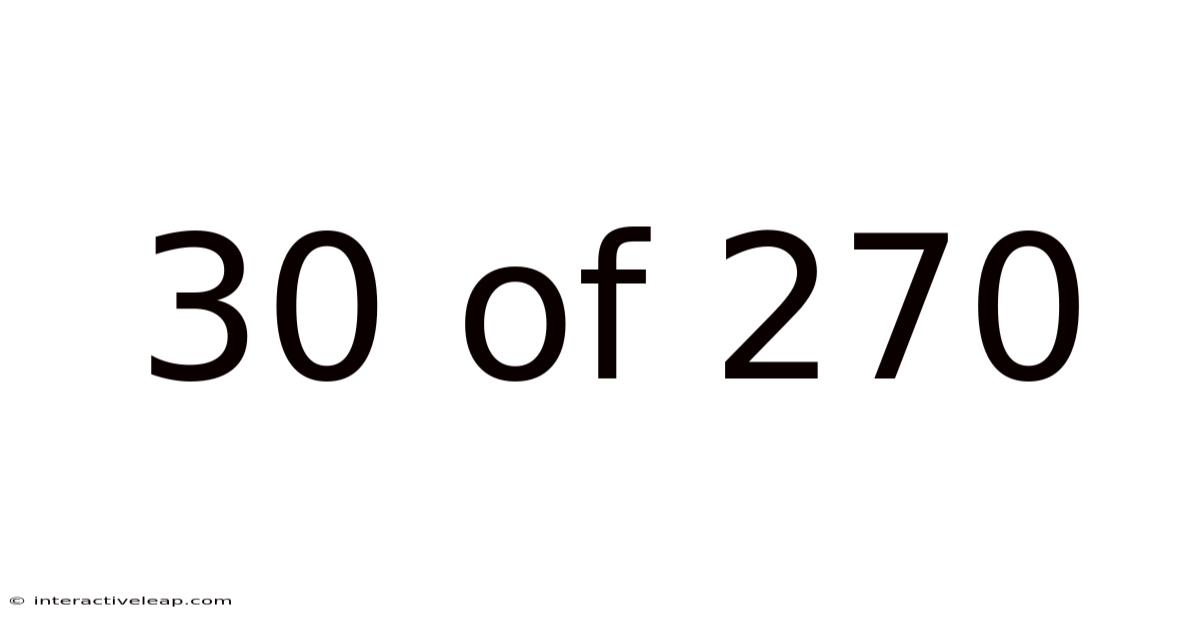
Table of Contents
Decoding the Mystery: Understanding the Fraction 30/270 and its Implications
The seemingly simple fraction 30/270 might appear insignificant at first glance. However, understanding this fraction opens doors to a deeper appreciation of mathematical concepts, particularly simplification, ratios, and their practical applications in various fields. This comprehensive guide will not only explain how to simplify 30/270 but will also explore its implications in different contexts, providing a solid foundation for understanding fractions and their relevance in everyday life.
Introduction: Why is 30/270 Important?
The fraction 30/270, while seemingly basic, serves as an excellent example to illustrate the importance of simplifying fractions and understanding their underlying ratios. Simplifying fractions makes them easier to understand and compare, facilitating calculations and interpretations. Moreover, the ratio represented by 30/270, once simplified, can be applied in numerous real-world scenarios, from calculating percentages to understanding proportions in various fields like cooking, construction, and even finance. This article will break down this fraction step-by-step, providing a clear understanding of its simplification and its broader implications.
Simplifying 30/270: A Step-by-Step Guide
Simplifying a fraction, also known as reducing a fraction to its lowest terms, involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. Let's simplify 30/270:
-
Find the GCD: The first step is to find the greatest common divisor (GCD) of 30 and 270. We can use several methods to find the GCD, including listing factors or using the Euclidean algorithm. Let's use the listing factors method:
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- Factors of 270: 1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270
The greatest common factor shared by both numbers is 30.
-
Divide both numerator and denominator by the GCD: Now that we've found the GCD (30), we divide both the numerator (30) and the denominator (270) by 30:
30 ÷ 30 = 1 270 ÷ 30 = 9
-
Simplified Fraction: Therefore, the simplified fraction is 1/9.
This means that 30/270 and 1/9 represent the same value; they are equivalent fractions. The simplified version, 1/9, is much easier to work with in calculations and comparisons.
Understanding the Ratio: What does 1/9 tell us?
The simplified fraction 1/9 represents a ratio. It tells us that for every 9 parts, 1 part is represented by the numerator. This ratio can be interpreted in many ways depending on the context. For instance:
-
Percentage: 1/9 can be easily converted to a percentage by dividing the numerator by the denominator and multiplying by 100: (1 ÷ 9) x 100 ≈ 11.11%. This means that 30 out of 270 represents approximately 11.11%.
-
Proportions: The ratio 1/9 can be used to determine proportions in various scenarios. If you have a total of 270 items, 1/9 of those items would be 30. Similarly, if you know that 1/9 of a quantity is 30, you can determine the total quantity by multiplying 30 by 9, which equals 270.
-
Scaling: In scaling projects, this ratio can be useful. If you have a model that is 1/9 the size of the real thing, you can use the ratio to scale the dimensions up or down.
Real-World Applications of the Ratio 1/9
The simplicity of the 1/9 ratio makes it applicable across a wide range of fields:
-
Cooking: Imagine a recipe that calls for 270 grams of flour and 30 grams of sugar. The ratio of sugar to flour is 30/270, which simplifies to 1/9. You can easily adjust the recipe by maintaining this ratio. If you only have 90 grams of flour, you'd need 10 grams of sugar (1/9 of 90).
-
Construction: In construction, ratios are crucial for maintaining proportions and ensuring structural integrity. The 1/9 ratio might be relevant when mixing concrete or calculating material requirements for a specific structure.
-
Finance: In finance, ratios are used to analyze financial statements and assess the financial health of a company. The 1/9 ratio could be relevant in comparing different financial metrics.
-
Science: In many scientific experiments, precise ratios are essential. This ratio could be relevant in various chemical or biological experiments where specific proportions of substances are required.
Further Exploration: Fractions and their Significance
The fraction 30/270 and its simplified form, 1/9, highlight the importance of understanding and manipulating fractions. Fractions are fundamental to mathematics and are extensively used in many aspects of life. Here's a deeper look into the broader significance of fractions:
-
Foundation of Arithmetic: Fractions are a cornerstone of arithmetic, forming the basis for operations like addition, subtraction, multiplication, and division. Mastering fractions is crucial for progressing to more advanced mathematical concepts.
-
Decimal Representation: Every fraction can be represented as a decimal. 1/9, for example, is equivalent to 0.111... (a repeating decimal). Understanding this equivalence is important for converting between fractions and decimals.
-
Percentage Calculations: As demonstrated earlier, fractions are directly related to percentages. Understanding how to convert fractions to percentages and vice versa is essential for various applications, from calculating discounts to analyzing statistical data.
-
Ratio and Proportion: Fractions are intrinsically linked to ratios and proportions. Understanding these concepts is critical for solving problems involving scaling, mixing, and comparison.
Frequently Asked Questions (FAQ)
Q1: Are there other methods to simplify 30/270?
A1: Yes, besides listing factors, you can use the Euclidean algorithm to find the GCD. The Euclidean algorithm is a more efficient method for finding the GCD of larger numbers.
Q2: What if I made a mistake in finding the GCD?
A2: If you make a mistake in finding the GCD, your simplified fraction will not be in its lowest terms. You'll have to re-check your work and find the correct GCD to simplify the fraction accurately.
Q3: Can all fractions be simplified?
A3: Not all fractions can be simplified. If the numerator and the denominator share no common factors other than 1, the fraction is already in its simplest form. For example, the fraction 7/11 is already simplified.
Q4: Why is simplifying fractions important?
A4: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also provides a clearer representation of the ratio between the numerator and the denominator.
Conclusion: The Power of Simplicity
The seemingly simple fraction 30/270, when simplified to 1/9, reveals a powerful concept: the importance of simplification and understanding ratios. This seemingly small fraction provides a gateway to comprehending deeper mathematical concepts and their applications in the real world. By understanding the steps involved in simplifying fractions and the significance of the resulting ratio, we can enhance our problem-solving abilities and gain a better appreciation for the practical applications of mathematics in various fields. Remember, the ability to simplify fractions is not just a mathematical skill; it's a valuable tool applicable across numerous domains of life. This understanding empowers us to tackle complex problems with clarity and efficiency. From everyday tasks to intricate scientific endeavors, the mastery of fractions and their underlying principles provides a solid foundation for success.
Latest Posts
Latest Posts
-
45 Of 20
Sep 19, 2025
-
144lb In Kg
Sep 19, 2025
-
1 96cm In Feet
Sep 19, 2025
-
Double Eagle Coin
Sep 19, 2025
-
4 5 X 5
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 30 Of 270 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.