3/8 Of 48
interactiveleap
Sep 13, 2025 · 6 min read
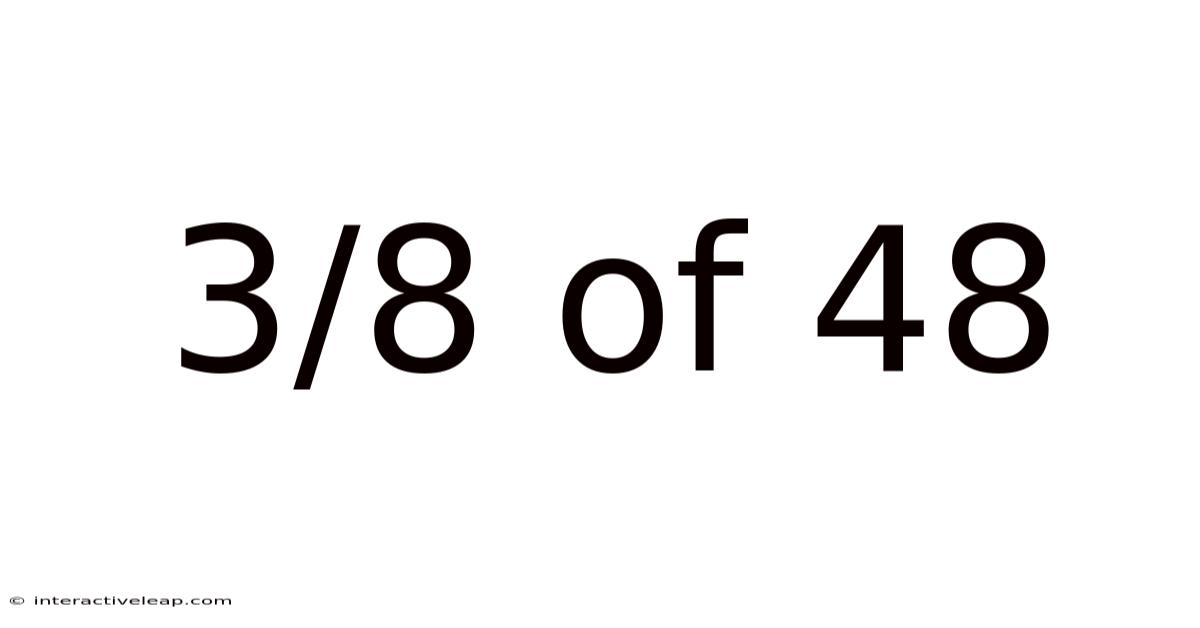
Table of Contents
Unveiling the Mystery: A Deep Dive into 3/8 of 48
Finding 3/8 of 48 might seem like a simple arithmetic problem, suitable only for elementary school. However, this seemingly straightforward calculation opens a door to a deeper understanding of fractions, proportions, and their real-world applications. This article will not only solve the problem but will also explore the underlying concepts, provide multiple solution methods, and delve into the broader implications of fractional calculations. We will even touch upon how this seemingly simple calculation relates to advanced mathematical concepts. This comprehensive guide is perfect for anyone wanting to solidify their understanding of fractions or simply curious to explore the mathematical beauty hidden within this seemingly simple equation.
Understanding Fractions: A Quick Refresher
Before we tackle 3/8 of 48, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we are considering 3 out of 8 equal parts of a whole.
Method 1: Direct Calculation – The Classic Approach
The most straightforward way to calculate 3/8 of 48 is to directly apply the concept of fractions. We can express "3/8 of 48" as a multiplication problem:
(3/8) * 48
To perform this calculation, we multiply the numerator (3) by 48 and then divide the result by the denominator (8):
(3 * 48) / 8 = 144 / 8 = 18
Therefore, 3/8 of 48 is 18.
Method 2: Simplification Before Calculation – Efficiency Matters
A slightly more efficient approach involves simplifying the fraction before performing the multiplication. Notice that 48 is divisible by 8:
48 / 8 = 6
Now, we can rewrite the original problem as:
3 * (48/8) = 3 * 6 = 18
This method reduces the size of the numbers involved, making the calculation simpler and less prone to errors. This approach highlights the importance of recognizing common factors and simplifying expressions before tackling complex calculations.
Method 3: Visual Representation – Understanding the Concept
For a visual approach, imagine a rectangular bar representing the whole number 48. We divide this bar into 8 equal parts. Each part represents 48/8 = 6. Since we want 3/8 of 48, we simply select three of these equal parts: 6 + 6 + 6 = 18. This method provides a concrete representation of the fraction and helps in understanding the concept intuitively. This is particularly helpful for beginners who are still grappling with the abstract nature of fractions.
Method 4: Proportion and Cross-Multiplication – A Broader Perspective
This problem can also be solved using proportions. We can set up a proportion where x represents 3/8 of 48:
3/8 = x/48
To solve for x, we use cross-multiplication:
8x = 3 * 48
8x = 144
x = 144 / 8
x = 18
This method demonstrates the power of proportions in solving problems involving fractions and ratios. It’s a valuable technique that extends far beyond this specific problem, finding applications in various fields like scaling recipes, converting units, and solving geometric problems.
Exploring Real-World Applications: Fractions in Everyday Life
Understanding fractions isn’t just about solving math problems; it’s crucial for navigating everyday situations. Consider these examples:
-
Cooking and Baking: Recipes often use fractions – 1/2 cup of sugar, 3/4 teaspoon of salt. Accurate measurements are essential for successful results. The ability to quickly calculate fractions ensures your culinary creations turn out perfectly.
-
Shopping and Budgeting: Discounts are often expressed as fractions or percentages. Understanding fractions allows you to quickly determine the final price after a discount. Similarly, managing a budget effectively often involves dividing resources into fractions to allocate funds for different expenses.
-
Measurement and Construction: Many construction and engineering projects require precise measurements. Understanding fractions is essential for accurately measuring materials and ensuring the structural integrity of buildings and other structures.
-
Data Analysis and Statistics: Fractions and proportions play a critical role in interpreting data. For instance, understanding the fraction of a population that holds a particular opinion is essential for accurate social and market research.
Beyond the Basics: Connecting to Advanced Mathematical Concepts
The simple problem of finding 3/8 of 48 subtly connects to more advanced mathematical concepts. These include:
-
Algebra: The proportion method used earlier is a fundamental concept in algebra, involving solving equations with unknowns.
-
Calculus: The concept of limits, a cornerstone of calculus, is fundamentally about approaching a value through increasingly smaller increments – similar to the idea of dividing a whole into smaller and smaller fractions.
-
Probability and Statistics: Fractions are intrinsically linked to probability and statistics. The concept of probability often involves expressing the likelihood of an event as a fraction.
-
Number Theory: Understanding fractions and their properties contributes to a deeper understanding of number theory, including concepts like prime numbers, factorization, and divisibility.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Absolutely! While understanding the underlying principles is important, a calculator can certainly speed up the process, particularly with more complex fractional calculations.
Q: What if the fraction wasn't simplified? Would the answer still be the same?
A: Yes, the answer would remain the same. While simplifying beforehand makes the calculation easier, it doesn't affect the final result.
Q: Are there other ways to visualize this problem?
A: Yes, you could use a pie chart or a set of objects to represent the whole and its fractional parts. The key is to choose a representation that helps you understand the concept.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through various problems involving fractions, try different solution methods, and use visual aids to reinforce your understanding. Online resources and educational materials can also be invaluable.
Conclusion: Mastering Fractions – A Stepping Stone to Mathematical Proficiency
Finding 3/8 of 48 is more than just a simple calculation; it's a gateway to understanding fundamental mathematical principles. Mastering fractions provides a strong foundation for tackling more complex mathematical concepts in algebra, calculus, statistics, and beyond. This seemingly simple problem emphasizes the importance of understanding the underlying concepts, choosing efficient methods, and visualizing mathematical problems to achieve a deeper level of comprehension. The ability to perform these calculations confidently opens doors to a wider range of applications in various aspects of life, from everyday tasks to specialized fields. Remember, the journey to mastering mathematics is a process of continuous learning and exploration. So, embrace the challenge, and enjoy the rewarding experience of unlocking the mathematical mysteries hidden within seemingly simple equations.
Latest Posts
Latest Posts
-
Poacher Turned Gamekeeper
Sep 13, 2025
-
7 5 To Fraction
Sep 13, 2025
-
Admission Point Score
Sep 13, 2025
-
2 Of 400
Sep 13, 2025
-
155lb To Kg
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3/8 Of 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.