3/8 Of 40
interactiveleap
Sep 17, 2025 · 6 min read
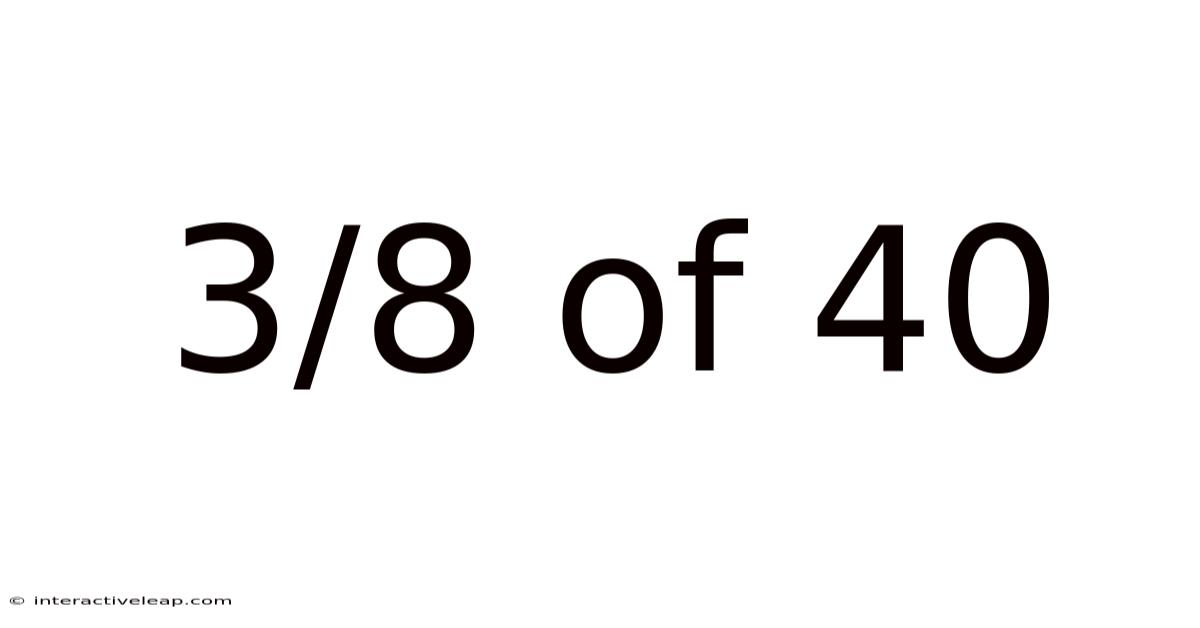
Table of Contents
Unveiling the Mystery: A Deep Dive into 3/8 of 40
Finding 3/8 of 40 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation offers a fantastic opportunity to explore fundamental mathematical concepts, delve into various solution methods, and even touch upon the broader applications of fractions in everyday life. This article will guide you through a comprehensive understanding of this calculation, moving beyond the simple answer to explore the underlying principles and practical implications. We'll cover different approaches to solving the problem, discuss the importance of understanding fractions, and even explore some related, more complex scenarios. By the end, you'll not only know the answer to 3/8 of 40 but also possess a deeper, more intuitive grasp of fraction arithmetic.
Understanding Fractions: The Building Blocks
Before we jump into calculating 3/8 of 40, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In our problem, 3/8, '3' is the numerator, and '8' is the denominator. This means we're interested in 3 out of 8 equal parts.
Think of a pizza cut into 8 equal slices. 3/8 of the pizza would mean you have 3 of those 8 slices. Understanding this visual representation can significantly simplify the process of working with fractions.
Method 1: Direct Calculation – The "Multiplication is Your Friend" Approach
The most straightforward method to find 3/8 of 40 involves multiplying the fraction by the whole number. We simply multiply the numerator (3) by 40 and then divide the result by the denominator (8).
- Step 1: Multiply the numerator by the whole number: 3 * 40 = 120
- Step 2: Divide the result by the denominator: 120 / 8 = 15
Therefore, 3/8 of 40 is 15.
Method 2: Finding One-Eighth First – The "Divide and Conquer" Strategy
This approach involves finding the value of one-eighth (1/8) of 40 first and then multiplying that value by 3 to get 3/8.
- Step 1: Divide the whole number by the denominator: 40 / 8 = 5 (This gives us the value of 1/8 of 40)
- Step 2: Multiply the result by the numerator: 5 * 3 = 15
Again, we arrive at the answer: 3/8 of 40 is 15. This method is particularly helpful when dealing with larger numbers or more complex fractions, as it breaks the problem down into smaller, more manageable steps.
Method 3: Simplifying the Fraction – The "Efficiency Expert" Approach
Before performing the calculation, we can sometimes simplify the fraction. While not necessary in this specific case, it’s a valuable skill to understand. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
In our example, 3/8 is already in its simplest form because 3 and 8 share no common divisors other than 1. However, let's consider an example where simplification would be useful. If the problem were to find 6/12 of 40, we would first simplify 6/12 to 1/2. Then, we would calculate 1/2 of 40, which is 20.
Beyond the Calculation: Real-World Applications of Fractions
Understanding fractions isn't just about solving math problems; it's a fundamental skill with countless real-world applications. Let's consider a few examples:
- Cooking and Baking: Recipes often use fractions (e.g., 1/2 cup of sugar, 2/3 cup of flour). Accurate fraction calculations are essential for achieving the desired results.
- Construction and Engineering: Precise measurements and calculations involving fractions are crucial in building structures, designing machines, and ensuring projects are completed accurately.
- Finance and Budgeting: Understanding fractions is essential for managing personal finances, calculating interest rates, and comprehending percentages (which are simply fractions expressed as a part of 100).
- Data Analysis: Many data analysis techniques involve working with proportions and ratios, which are fundamentally based on the concepts of fractions.
Expanding the Concept: Working with More Complex Fractions
Let's explore some more challenging scenarios to solidify our understanding of fraction calculations:
- Finding a Fraction of a Fraction: Imagine you need to find 1/4 of 3/8 of 40. This involves a two-step process: first, find 3/8 of 40 (which we already know is 15), and then find 1/4 of 15, which is 15/4 or 3.75.
- Fractions with Larger Numbers: Let's say we need to find 7/12 of 288. This could be solved using either method 1 or 2, resulting in an answer of 168. The "Divide and Conquer" method might be more manageable here.
- Mixed Numbers: Mixed numbers combine a whole number and a fraction (e.g., 2 1/2). To work with mixed numbers, first convert them to improper fractions (where the numerator is larger than the denominator). For example, 2 1/2 is equal to 5/2.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to understand fractions?
- A: Fractions are fundamental to many aspects of mathematics and have wide-ranging applications in everyday life, from cooking to finance to engineering. A strong understanding of fractions is crucial for success in many academic and professional fields.
-
Q: What if the denominator doesn't divide evenly into the whole number?
- A: If the denominator doesn't divide evenly into the whole number, the result will be a fraction or a decimal. For example, 1/3 of 10 is 10/3, which is approximately 3.33.
-
Q: Can I use a calculator for these calculations?
- A: Yes, calculators can be used to simplify the calculations, particularly when dealing with larger numbers or more complex fractions. However, understanding the underlying principles is essential for building a strong mathematical foundation.
-
Q: Are there other methods to solve this type of problem?
- A: Yes, depending on the context and the numbers involved, other methods might be more efficient. These could include using proportions, converting fractions to decimals, or employing visual aids like diagrams.
Conclusion: Mastering Fractions – A Journey Worth Taking
Finding 3/8 of 40 might seem trivial at first glance, but delving into the process reveals the richness and importance of understanding fractions. This seemingly simple calculation provides a stepping stone to mastering more complex mathematical concepts and applying those skills to diverse real-world situations. By understanding the different methods, exploring real-world applications, and tackling more challenging scenarios, you'll not only know that 3/8 of 40 is 15 but also build a strong foundation in fractional arithmetic – a skill that will serve you well throughout your life. Remember, the key is not just getting the right answer but also understanding the why behind the calculation. So keep practicing, keep exploring, and keep expanding your mathematical horizons!
Latest Posts
Latest Posts
-
Diet Coke Pink
Sep 17, 2025
-
Transpiration Vs Translocation
Sep 17, 2025
-
25 Of 1400
Sep 17, 2025
-
18 8kg In Stone
Sep 17, 2025
-
Battery With Indicator
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3/8 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.