3/8 Of 24
interactiveleap
Sep 17, 2025 · 6 min read
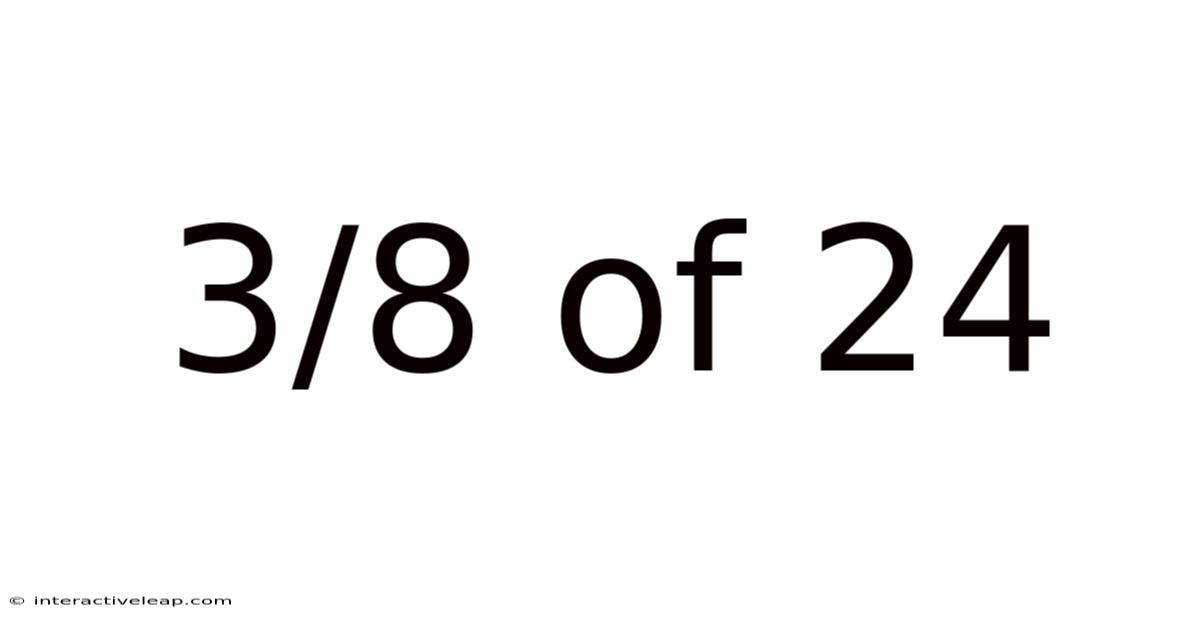
Table of Contents
Unveiling the Mystery: A Deep Dive into 3/8 of 24
Finding 3/8 of 24 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation offers a fascinating gateway to explore fundamental mathematical concepts, including fractions, multiplication, and their real-world applications. This article will not only solve the problem but also delve into the underlying principles, providing a comprehensive understanding for learners of all levels. We'll explore different methods of solving the problem, discuss the significance of fractions in everyday life, and even touch upon some advanced concepts related to proportional reasoning.
Understanding Fractions: The Building Blocks
Before we tackle the problem of finding 3/8 of 24, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, 3/8 means we have 3 parts out of a total of 8 equal parts.
Imagine a pizza cut into 8 equal slices. 3/8 of the pizza would represent 3 of those 8 slices. Understanding this visual representation is crucial for grasping the concept of fractions and applying it to real-world scenarios. This intuitive approach makes fractions less abstract and more relatable.
Method 1: Direct Multiplication
The most straightforward method to find 3/8 of 24 is through direct multiplication. We can express "of" as multiplication. Therefore, 3/8 of 24 can be written as:
(3/8) * 24
To solve this, we can multiply the numerator (3) by 24 and then divide the result by the denominator (8):
(3 * 24) / 8 = 72 / 8 = 9
Therefore, 3/8 of 24 is 9. This method is efficient and readily applicable to similar problems involving fractions and whole numbers.
Method 2: Simplifying Before Multiplication
A slightly more advanced approach involves simplifying the fraction before performing the multiplication. We can observe that 8 and 24 share a common factor, which is 8. We can simplify the fraction by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 8 in this case:
(3/8) * 24 can be simplified to:
3 * (24/8) = 3 * 3 = 9
This method reduces the complexity of the calculation by simplifying the fraction first, making it easier to compute the final answer. This approach is particularly useful when dealing with larger numbers or more complex fractions.
Method 3: Finding a Fraction of a Whole by Division and Multiplication
Another way to approach this problem is by first dividing the whole number (24) by the denominator (8) to find the value of one-eighth, then multiplying the result by the numerator (3).
24 / 8 = 3 (This is the value of 1/8 of 24)
3 * 3 = 9 (This is the value of 3/8 of 24)
This method emphasizes the meaning of the fraction as a part of a whole, providing a more conceptual understanding of the calculation. This approach is highly effective in visualizing the problem and breaking it down into smaller, more manageable steps.
Real-World Applications: Fractions in Everyday Life
Fractions are not just abstract mathematical concepts; they are integral to our daily lives. We encounter them in various contexts, including:
- Cooking: Recipes often involve fractional measurements, such as 1/2 cup of sugar or 2/3 cup of flour.
- Shopping: Discounts and sales are frequently expressed as fractions, such as a 1/4 off sale or a 2/5 reduction in price.
- Construction and Engineering: Precision in building and engineering relies heavily on fractional measurements to ensure accuracy and stability.
- Time: Telling time involves fractions; 15 minutes is 1/4 of an hour, while 30 minutes is 1/2 an hour.
- Data Analysis: Fractions are essential in statistical analysis and probability calculations.
Understanding and working with fractions is therefore essential for effective problem-solving in many real-world situations.
Expanding the Understanding: Proportional Reasoning
The problem of finding 3/8 of 24 can be extended to the broader concept of proportional reasoning. Proportional reasoning involves understanding the relationship between quantities and how they change proportionally. This is a critical skill applicable to many mathematical and real-world problems.
For example, if we know that 3/8 of 24 is 9, we can use this information to solve similar problems involving proportional relationships. If we need to find 6/8 (or 3/4) of 24, we can simply double the value of 3/8 of 24 (which is 9), resulting in 18. This demonstrates how understanding one proportional relationship can help us solve others.
Beyond the Basics: Working with More Complex Fractions
While our example uses a relatively simple fraction, the principles discussed apply to more complex scenarios. For example, finding 7/12 of 36 involves the same fundamental principles of multiplication and division, although the calculation might be slightly more involved. The key is to understand the meaning of the fraction and to apply the appropriate method for solving the problem. Mastering these skills builds a solid foundation for tackling more advanced mathematical concepts.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, absolutely. Calculators can efficiently handle fraction calculations. However, understanding the underlying principles is crucial, even when using technology.
Q: What if the fraction and the whole number don't have a common factor?
A: Even if there's no common factor, the direct multiplication method still works effectively. For example, finding 2/5 of 17 would be (2*17)/5 = 34/5 = 6.8.
Q: Are there other ways to represent 3/8 of 24?
A: Yes, the result can be represented as a decimal (9.0), a percentage (9/24 *100% = 37.5%), or even as a ratio (9:24, which can be simplified to 3:8).
Q: How can I improve my understanding of fractions?
A: Practice is key. Try solving various problems involving fractions, from simple to more complex ones. Visual aids, like diagrams and real-world examples, can significantly improve comprehension.
Conclusion: Mastering Fractions – A Stepping Stone to Success
Finding 3/8 of 24, while seemingly simple, provides a valuable opportunity to explore and reinforce our understanding of fractions, multiplication, and proportional reasoning. These fundamental mathematical concepts are essential building blocks for more advanced mathematical studies and are frequently applied in everyday life. By understanding the different methods for solving this problem and its real-world applications, we can appreciate the importance of fractions and develop a stronger mathematical foundation. Continue to practice, explore various problem-solving strategies, and never hesitate to delve deeper into the mathematical concepts that fascinate you. The journey of mathematical discovery is a rewarding one, filled with endless possibilities and applications. Remember, consistent practice and a curious mind are the keys to unlocking your full mathematical potential.
Latest Posts
Latest Posts
-
Diet Coke Pink
Sep 17, 2025
-
Transpiration Vs Translocation
Sep 17, 2025
-
25 Of 1400
Sep 17, 2025
-
18 8kg In Stone
Sep 17, 2025
-
Battery With Indicator
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3/8 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.