3/5 Of 240
interactiveleap
Sep 17, 2025 · 5 min read
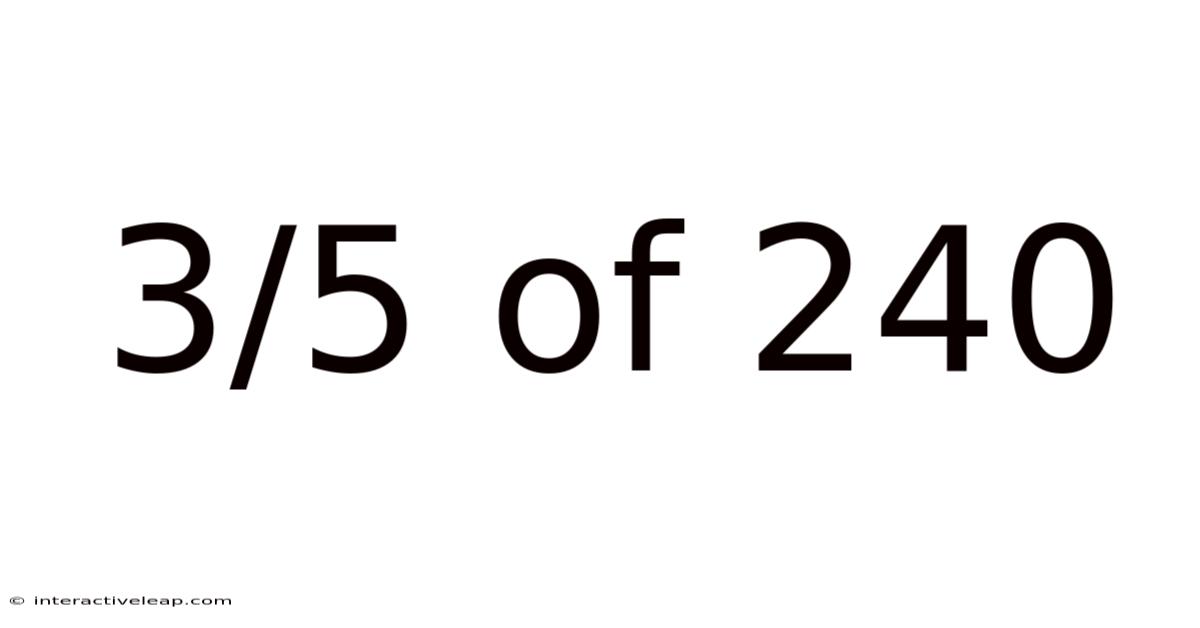
Table of Contents
Decoding 3/5 of 240: A Deep Dive into Fractions and Their Applications
Finding 3/5 of 240 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation unlocks a deeper understanding of fractions, their practical applications in everyday life, and even more advanced mathematical concepts. This article will not only solve the problem but also explore the underlying principles, provide multiple approaches to solving similar problems, and delve into real-world examples where such calculations are crucial. This comprehensive guide will leave you with a robust understanding of fractions and their significant role in various fields.
Understanding Fractions: A Foundation
Before tackling 3/5 of 240, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows the total number of equal parts the whole is divided into. In the fraction 3/5, 3 is the numerator, and 5 is the denominator. This means we're considering 3 parts out of a total of 5 equal parts.
Method 1: Direct Calculation – Multiplying Fractions and Whole Numbers
The most straightforward way to find 3/5 of 240 is to multiply the fraction by the whole number. Remember that a whole number can be written as a fraction with a denominator of 1 (e.g., 240 = 240/1). Therefore, our calculation becomes:
(3/5) * (240/1) = (3 * 240) / (5 * 1) = 720 / 5
Now, we simply divide 720 by 5:
720 / 5 = 144
Therefore, 3/5 of 240 is 144.
Method 2: Finding the Unit Fraction – A Step-by-Step Approach
This method involves first finding 1/5 of 240 and then multiplying the result by 3. This approach is particularly helpful for visualizing the problem and is often easier for beginners to grasp.
-
Find 1/5 of 240: To find one-fifth, we divide 240 by 5:
240 / 5 = 48
-
Find 3/5 of 240: Since we now know that 1/5 of 240 is 48, we multiply this value by 3 to find 3/5:
48 * 3 = 144
Again, we arrive at the answer: 3/5 of 240 is 144.
Method 3: Converting the Fraction to a Decimal – Using Decimal Multiplication
We can convert the fraction 3/5 into a decimal by dividing the numerator by the denominator:
3 / 5 = 0.6
Now, we multiply this decimal by 240:
0.6 * 240 = 144
This method provides an alternative approach, especially useful when working with calculators or when dealing with more complex fractions that are easily converted to decimals.
Real-World Applications: Where Fractions Matter
The seemingly simple calculation of 3/5 of 240 has numerous real-world applications across various fields:
-
Business and Finance: Calculating discounts, profit margins, and sales tax often involves fractional calculations. For example, a store offering a 3/5 discount on a $240 item would reduce the price by $144.
-
Engineering and Construction: Fractions are essential for precise measurements and calculations in blueprints and construction projects. Determining the amount of materials needed based on fractional proportions is crucial for accurate estimations and project success.
-
Cooking and Baking: Recipes often use fractional measurements (e.g., 1/2 cup, 2/3 teaspoon). Accurately calculating these fractions ensures that the dish turns out correctly. Scaling up or down recipes requires a clear understanding of fractional proportions.
-
Data Analysis and Statistics: Fractions and percentages (which are essentially fractions with a denominator of 100) are fundamental to interpreting and presenting data. Understanding proportions and ratios are crucial for making informed decisions based on statistical analysis.
-
Everyday Life: Sharing items equally among friends, calculating portions of a bill, or understanding discounts at the mall – all involve working with fractions. These simple, yet vital, calculations influence our daily choices and transactions.
Expanding the Concept: Working with More Complex Fractions
While we focused on 3/5 of 240, the principles apply to any fraction and whole number. Let's consider a slightly more complex example: finding 7/8 of 320.
-
Direct Calculation: (7/8) * (320/1) = (7 * 320) / (8 * 1) = 2240 / 8 = 280
-
Unit Fraction Method: 1/8 of 320 is 320 / 8 = 40. Therefore, 7/8 of 320 is 40 * 7 = 280
-
Decimal Conversion Method: 7/8 = 0.875. 0.875 * 320 = 280
Frequently Asked Questions (FAQ)
-
Q: What if the fraction and whole number don't simplify easily? A: You can still use the direct multiplication method, even if the resulting fraction requires more complex division. Calculators are helpful in these instances.
-
Q: Can I use mixed numbers (like 1 1/2) in these calculations? A: Yes, convert the mixed number into an improper fraction first (in this case, 3/2) and then proceed with the multiplication.
-
Q: What if I need to find a fraction of a fraction? A: Simply multiply the numerators together and the denominators together. For example, (1/2) * (2/3) = (12) / (23) = 2/6 = 1/3.
-
Q: Are there other methods to solve these types of problems? A: Yes, depending on the specific numbers involved, alternative approaches such as using proportions or ratios might be more efficient.
Conclusion: Mastering Fractions for a Brighter Future
Mastering fractions is not just about solving simple arithmetic problems; it's about developing a crucial skillset applicable across numerous domains. From managing personal finances to tackling complex engineering challenges, the ability to work confidently with fractions is an essential tool for success. This article has demonstrated various methods for solving problems involving fractions and whole numbers, providing a solid foundation for further exploration of mathematical concepts. By understanding the underlying principles and practicing different approaches, you can confidently navigate the world of fractions and unlock a deeper appreciation for their practical relevance. The seemingly simple calculation of 3/5 of 240 serves as a springboard to a much broader understanding of this fundamental mathematical concept. Remember, consistent practice and a curious mindset are key to mastering fractions and applying them effectively in your life.
Latest Posts
Latest Posts
-
60 Of 32
Sep 18, 2025
-
127km In Miles
Sep 18, 2025
-
Patterns And Numbers
Sep 18, 2025
-
360g In Oz
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3/5 Of 240 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.