3/10 + 0.5
interactiveleap
Sep 22, 2025 · 6 min read
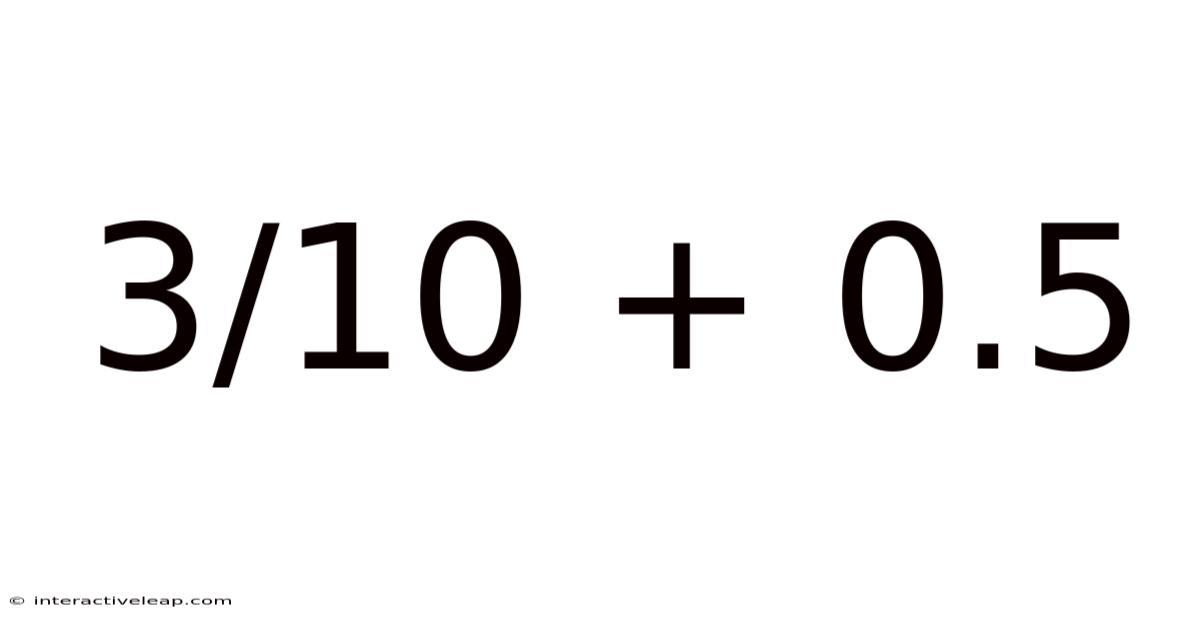
Table of Contents
Decoding 3/10 + 0.5: A Deep Dive into Fraction and Decimal Addition
This article will comprehensively explore the seemingly simple mathematical problem: 3/10 + 0.5. While the calculation itself is straightforward, unraveling it provides a valuable opportunity to reinforce fundamental concepts in fractions, decimals, and their interconversion. We will not only solve the problem but also delve into the underlying principles, providing a solid foundation for anyone looking to strengthen their mathematical skills. Understanding this seemingly simple equation unlocks a deeper understanding of number systems and their manipulation.
Introduction: Bridging the Gap Between Fractions and Decimals
The problem 3/10 + 0.5 presents a common scenario in mathematics: adding a fraction and a decimal. This requires a firm grasp of both number systems and the ability to seamlessly convert between them. Many find this transition challenging, but mastering it is crucial for success in more complex mathematical applications. This article aims to demystify this process, providing a step-by-step guide and illuminating the underlying logic. We'll cover various methods for solving the problem, emphasizing conceptual understanding over rote memorization.
Understanding Fractions and Decimals
Before diving into the solution, let's refresh our understanding of fractions and decimals.
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/10, 3 is the numerator and 10 is the denominator. This means we have 3 parts out of a total of 10 equal parts.
-
Decimals: A decimal is another way of representing a part of a whole. It uses a base-ten system, where each digit to the right of the decimal point represents a decreasing power of ten. The first digit after the decimal point represents tenths (1/10), the second represents hundredths (1/100), and so on. For example, 0.5 is equivalent to 5/10 or one-half.
Method 1: Converting the Fraction to a Decimal
The most straightforward approach to solving 3/10 + 0.5 is to convert the fraction 3/10 into its decimal equivalent. Since the denominator is 10, this is a simple conversion:
3/10 = 0.3
Now we can add the two decimals:
0.3 + 0.5 = 0.8
Therefore, the solution to 3/10 + 0.5 is 0.8.
Method 2: Converting the Decimal to a Fraction
Alternatively, we can convert the decimal 0.5 into a fraction and then add the two fractions. Since 0.5 represents five-tenths, we can write it as:
0.5 = 5/10
Now we add the two fractions:
3/10 + 5/10 = (3+5)/10 = 8/10
This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
8/10 = (8÷2)/(10÷2) = 4/5
Therefore, the solution, expressed as a fraction, is 4/5. Note that 4/5 is equivalent to 0.8, demonstrating the equivalence between the two representations.
Method 3: Finding a Common Denominator (for Fractions)
If we choose to work entirely with fractions, we can find a common denominator for 3/10 and the fractional equivalent of 0.5 (which is 5/10). Since both fractions already have a common denominator of 10, we can proceed directly with the addition:
3/10 + 5/10 = 8/10
As shown in Method 2, this simplifies to 4/5 or 0.8.
Visual Representation: Understanding the Concepts
Imagine a pizza cut into 10 equal slices. The fraction 3/10 represents 3 slices of the pizza. The decimal 0.5, or 5/10, represents 5 slices. Adding these together (3 slices + 5 slices) gives you 8 slices out of 10, or 8/10, which simplifies to 4/5 of the pizza. This visual representation makes the addition more intuitive and concrete.
The Importance of Decimal Places and Significant Figures
In calculations involving decimals, paying close attention to decimal places and significant figures is crucial, particularly in scientific and engineering applications. While the addition 3/10 + 0.5 is relatively simple, more complex calculations might involve rounding to a specific number of decimal places to maintain accuracy and prevent the accumulation of insignificant digits. This is an important consideration in fields where precision is paramount.
Expanding the Concept: Adding More Complex Fractions and Decimals
The principles discussed here extend to more intricate problems involving the addition of multiple fractions and decimals. The key steps remain consistent:
-
Convert all numbers to either fractions or decimals. Choose the representation that seems most convenient for the given problem.
-
Find a common denominator (if working with fractions). This allows you to add the numerators directly.
-
Simplify the result (if necessary). Reduce fractions to their simplest form and round decimals to the appropriate number of significant figures.
For example, consider the problem 1/4 + 0.25 + 2/5. You could convert all to decimals (0.25 + 0.25 + 0.4 = 0.9) or find a common denominator for the fractions (5/20 + 5/20 + 8/20 = 18/20 = 9/10 = 0.9).
Frequently Asked Questions (FAQ)
Q: Why is it important to be able to convert between fractions and decimals?
A: Converting between fractions and decimals is essential for solving a wide range of mathematical problems. It allows you to use the most convenient representation for a particular calculation and ensures seamless transitions between different number systems. This skill is fundamental for higher-level mathematics and its applications in various fields.
Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator to solve 3/10 + 0.5. Most calculators handle both fractions and decimals. However, understanding the underlying principles is crucial for developing a strong mathematical foundation. Using a calculator without comprehension only provides an answer; it does not build mathematical proficiency.
Q: What if the fractions have different denominators?
A: If the fractions have different denominators, you must first find a common denominator before adding them. This involves finding the least common multiple (LCM) of the denominators. For example, to add 1/3 + 1/4, you would find the LCM of 3 and 4, which is 12. Then, you would rewrite the fractions with a denominator of 12 before adding them (4/12 + 3/12 = 7/12).
Q: Are there any real-world applications of this type of calculation?
A: Yes! Adding fractions and decimals is used extensively in many real-world situations, such as calculating proportions in cooking, measuring distances, determining financial amounts, and solving problems in science and engineering. The ability to perform these calculations accurately and efficiently is a valuable skill in various contexts.
Conclusion: Mastering the Fundamentals
Solving 3/10 + 0.5 might appear trivial at first glance, but it serves as a potent illustration of fundamental mathematical concepts. Mastering the conversion between fractions and decimals, along with the ability to perform arithmetic operations on both, forms the cornerstone of more advanced mathematical skills. By understanding the underlying principles and practicing different methods, you can build a strong foundation for future mathematical endeavors. The ability to comfortably navigate between fractions and decimals is not just a mathematical skill; it’s a problem-solving tool applicable to countless aspects of life. This simple equation unlocks a world of numerical understanding, empowering you to tackle more complex challenges with confidence.
Latest Posts
Latest Posts
-
13 3stone In Kg
Sep 22, 2025
-
1200mg To Grams
Sep 22, 2025
-
250 Litres Gallons
Sep 22, 2025
-
15 18 Simplified
Sep 22, 2025
-
103 4kg In Stones
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3/10 + 0.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.