2x 5x 2
interactiveleap
Sep 20, 2025 · 7 min read
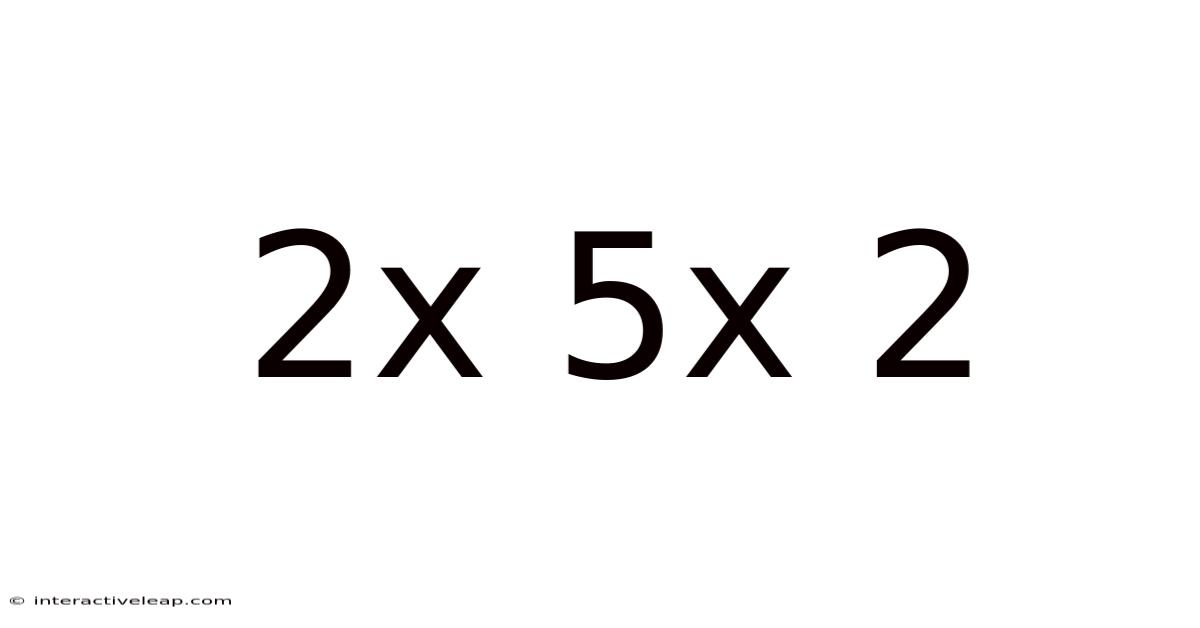
Table of Contents
Decoding the Mystery: Exploring the Mathematical Significance of "2 x 5 x 2"
The seemingly simple expression "2 x 5 x 2" might appear trivial at first glance. However, this seemingly innocuous equation holds a surprising depth, offering a gateway to explore fundamental concepts in mathematics, from basic arithmetic to more advanced applications. This article will delve into the various interpretations and implications of this expression, demonstrating its significance beyond a simple calculation. We’ll explore its use in different mathematical contexts, its relevance in real-world applications, and even touch upon its potential for inspiring further mathematical exploration.
Understanding the Fundamentals: Basic Arithmetic
At its core, "2 x 5 x 2" is a multiplication problem. Multiplication, one of the four basic arithmetic operations, represents repeated addition. In this case, we are essentially adding two five times and then doubling the result. The order of operations, dictated by the commutative and associative properties of multiplication, allows us to solve this in several ways:
- Method 1 (Left to Right): (2 x 5) x 2 = 10 x 2 = 20
- Method 2 (Right to Left): 2 x (5 x 2) = 2 x 10 = 20
- Method 3 (Rearranging Factors): 2 x 2 x 5 = 4 x 5 = 20
The result remains constant: 20. This consistency highlights the fundamental properties of multiplication – specifically, the commutative property (the order of the numbers doesn't matter) and the associative property (the grouping of the numbers doesn't matter). These properties are cornerstones of algebra and beyond.
Beyond the Basics: Applications in Geometry and Measurement
The expression "2 x 5 x 2" finds practical application in various geometrical calculations. Consider, for instance, calculating the volume of a rectangular prism (a box). If the dimensions of the box are 2 units by 5 units by 2 units, then the volume is simply the product of these three dimensions: 2 x 5 x 2 = 20 cubic units. This simple calculation has countless real-world applications, from packaging and shipping to construction and engineering.
Imagine calculating the amount of concrete needed for a foundation, the volume of a storage container, or even the space occupied by a stack of books. Understanding how to calculate volume, a direct application of "2 x 5 x 2" type calculations, is crucial in various fields. This extends to more complex shapes; calculating the volume of irregular shapes often involves breaking them down into simpler rectangular prisms, each requiring similar multiplicative calculations.
Exploring Number Theory: Prime Factorization and Divisibility
The expression "2 x 5 x 2" offers an excellent opportunity to delve into number theory. The numbers 2 and 5 are prime numbers – numbers greater than 1 that are divisible only by 1 and themselves. Prime factorization is the process of expressing a number as a product of its prime factors. In the case of 20 (the result of our calculation), the prime factorization is 2 x 2 x 5 or 2² x 5.
Understanding prime factorization is critical for various mathematical concepts, including:
- Finding the Greatest Common Divisor (GCD): Identifying the largest number that divides two or more numbers without leaving a remainder.
- Finding the Least Common Multiple (LCM): Determining the smallest number that is a multiple of two or more numbers.
- Simplifying Fractions: Expressing fractions in their lowest terms.
These concepts are fundamental to algebra, number theory, and even cryptography. The seemingly simple act of breaking down 20 into its prime factors unlocks a wealth of mathematical understanding.
Algebraic Expressions and Variables: Expanding the Scope
Moving beyond arithmetic, we can introduce variables to generalize the expression. Instead of fixed numbers, we can represent the dimensions with variables, say length (l), width (w), and height (h). The volume of a rectangular prism would then be represented by the algebraic expression l x w x h. Substituting specific values (like 2, 5, and 2) would yield the numerical result 20.
This algebraic representation allows us to analyze and manipulate the volume formula more flexibly. We can, for instance, solve for one dimension given the other two and the volume. This ability to use variables and equations to represent and solve problems is the cornerstone of algebra and is essential for problem-solving in numerous scientific and engineering disciplines.
Real-World Applications: Beyond Geometry
The principles behind "2 x 5 x 2" extend far beyond simple geometrical calculations. Consider these real-world examples:
- Cost Calculation: If a pack of pencils costs $2, and you buy 5 packs, the total cost is 2 x 5 = $10. If you buy two such sets, the total cost becomes 2 x 5 x 2 = $20.
- Production and Inventory: A factory produces 2 batches of a product daily, each batch containing 5 units. Over two days, the total production is 2 x 5 x 2 = 20 units.
- Data Analysis: Imagine a simple dataset with 2 categories, each with 5 sub-categories, and 2 data points per sub-category. The total number of data points would be 2 x 5 x 2 = 20.
These examples illustrate the wide applicability of this seemingly simple mathematical principle across various fields.
Mathematical Progression: Extending the Concept
The expression "2 x 5 x 2" can be used as a springboard to explore more complex mathematical concepts. For example:
- Exponents and Powers: We can rewrite the expression as 2² x 5, introducing the concept of exponents. This leads to a deeper understanding of exponential growth and decay, essential for understanding compound interest, population dynamics, and radioactive decay.
- Sequences and Series: The numbers 2, 5, and 2 could be seen as part of a sequence. Exploring different patterns and sequences leads to a broader understanding of mathematical patterns and relationships.
- Matrices and Linear Algebra: Matrices are rectangular arrays of numbers, and operations on matrices involve multiplications similar to what we see in "2 x 5 x 2". This opens up the world of linear algebra, vital in fields like computer graphics, data science, and physics.
These extensions demonstrate that even the simplest mathematical expressions can be stepping stones towards more sophisticated concepts.
Frequently Asked Questions (FAQ)
Q: What is the order of operations for solving "2 x 5 x 2"?
A: Due to the commutative and associative properties of multiplication, the order doesn't matter. You can solve it from left to right, right to left, or by rearranging the factors. The result will always be 20.
Q: Can this expression be used in division?
A: Yes, division is the inverse operation of multiplication. You could express the problem as 20 / 5 / 2 = 2 or 20 / 2 / 5 = 2.
Q: Are there any real-world situations where the order of multiplication does matter?
A: While the commutative property of multiplication holds true for pure numbers, the order might matter in real-world applications depending on the context. For instance, if you're calculating the volume of a rectangular prism, changing the order of the dimensions doesn’t affect the volume. However, in more complex scenarios involving matrices or other higher-level mathematical constructs, the order of operations can significantly influence the outcome.
Q: How can I use this concept to teach children about multiplication?
A: Use visual aids like blocks or counters to represent the numbers. Arrange them to physically demonstrate the repeated addition represented by multiplication.
Conclusion: The Enduring Power of Simplicity
The seemingly simple mathematical expression "2 x 5 x 2" unveils a surprising depth of mathematical concepts. From the fundamentals of arithmetic to the complexities of algebra, geometry, and number theory, this expression serves as a powerful illustration of how fundamental mathematical principles underpin a wide range of applications. Its simplicity belies its significance, reminding us that even the most basic concepts can hold profound mathematical power and unlock pathways to deeper understanding. By exploring this seemingly simple equation, we've uncovered its multifaceted nature and its potential for inspiring further mathematical exploration, reinforcing the importance of developing a strong foundation in mathematics for success in various fields.
Latest Posts
Latest Posts
-
Multiples Of Three
Sep 20, 2025
-
500kg In Pounds
Sep 20, 2025
-
Ewhurst Polo Club
Sep 20, 2025
-
Greenmeadow Community Farm
Sep 20, 2025
-
Microlitres To Millilitres
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 2x 5x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.