2x 1 7
interactiveleap
Sep 23, 2025 · 6 min read
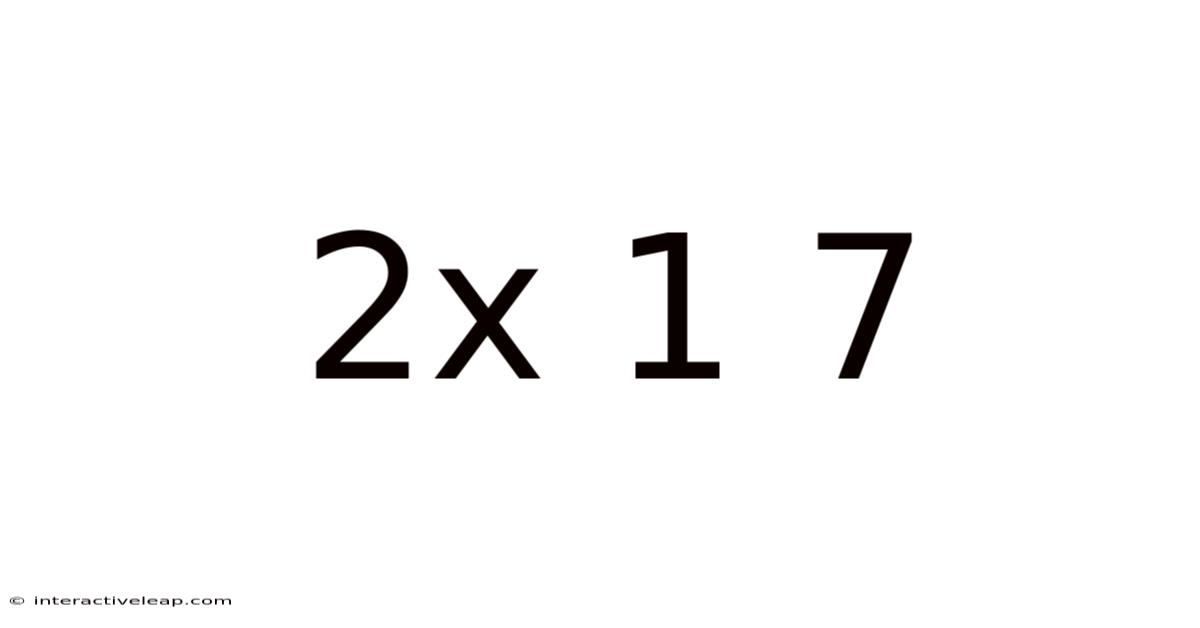
Table of Contents
Decoding the Enigma: Exploring the Mathematical and Philosophical Implications of "2x + 1 = 7"
This seemingly simple equation, 2x + 1 = 7, serves as a gateway to exploring fundamental concepts in algebra, problem-solving, and even philosophy. While its solution might seem trivial to those familiar with basic mathematics, a deeper dive reveals layers of meaning relevant to understanding mathematical logic, problem-solving strategies, and the very nature of mathematical truth. This article will unpack the equation, exploring its solution, its broader implications within mathematics, and its potential use in educational contexts.
Introduction: A Simple Equation, Profound Implications
The equation 2x + 1 = 7 is a linear equation, a cornerstone of elementary algebra. Its simplicity belies its importance. It provides a foundational understanding of:
- Variables: The 'x' represents an unknown value, a variable we need to find.
- Constants: The numbers 2, 1, and 7 are constants, fixed values.
- Operations: The equation uses addition and multiplication, basic arithmetic operations.
- Equality: The equals sign (=) indicates a balance or equivalence between the two sides of the equation.
Solving this equation is a crucial first step in developing algebraic reasoning skills. It introduces the concept of manipulating equations to isolate the variable, a skill crucial for tackling more complex mathematical problems later on.
Solving the Equation: A Step-by-Step Approach
Solving for 'x' involves a series of logical steps designed to isolate the variable on one side of the equation. Here's a step-by-step approach:
-
Subtract 1 from both sides: This maintains the balance of the equation. The equation becomes: 2x + 1 - 1 = 7 - 1, which simplifies to 2x = 6.
-
Divide both sides by 2: This isolates 'x'. The equation becomes: 2x / 2 = 6 / 2, which simplifies to x = 3.
Therefore, the solution to the equation 2x + 1 = 7 is x = 3. This means that if we substitute 3 for 'x' in the original equation, the left side will equal the right side: 2(3) + 1 = 7, which simplifies to 7 = 7. This confirms our solution.
Beyond the Solution: Exploring Mathematical Concepts
The solution itself is only the beginning. This simple equation opens doors to a deeper understanding of several key mathematical concepts:
-
Inverse Operations: Solving the equation relies heavily on inverse operations. Subtraction is the inverse of addition, and division is the inverse of multiplication. Understanding inverse operations is fundamental to manipulating equations and solving for unknowns.
-
Properties of Equality: The process of solving the equation relies implicitly on the properties of equality. Specifically, we used the addition property of equality (adding the same value to both sides) and the division property of equality (dividing both sides by the same non-zero value). These properties ensure that the equality remains true throughout the solution process.
-
Order of Operations (PEMDAS/BODMAS): While not explicitly used in solving this specific equation, understanding the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is crucial for solving more complex equations involving multiple operations.
-
Linear Equations and their Graphs: The equation 2x + 1 = 7 represents a line on a Cartesian coordinate system. Graphing linear equations helps visualize the relationship between the variables and the solution. The solution, x = 3, corresponds to the x-intercept of the line.
The Equation in Educational Contexts: Building Foundational Skills
The equation 2x + 1 = 7 is a valuable tool in educational settings for several reasons:
-
Introduction to Algebra: It serves as an excellent introductory problem for students learning algebra. Its simplicity allows students to focus on the fundamental concepts without getting bogged down in complex calculations.
-
Developing Problem-Solving Skills: Solving the equation requires a systematic approach, fostering the development of crucial problem-solving skills. Students learn to break down a problem into smaller, manageable steps and to check their work for accuracy.
-
Building Confidence: Successfully solving even a simple equation like this builds confidence and encourages students to tackle more challenging problems in the future.
-
Real-World Applications: While this specific equation might not have immediate real-world applications in its simplest form, the underlying principles are crucial for solving real-world problems that can be modeled using linear equations, such as calculating costs, determining distances, or analyzing rates of change.
Extending the Concept: Variations and More Complex Equations
While we’ve focused on 2x + 1 = 7, we can explore variations and extensions of this basic concept:
-
Changing the Constants: Altering the constants (2, 1, and 7) changes the solution. For example, 2x + 1 = 9 would yield x = 4. Exploring different constants provides practice and highlights the relationship between the constants and the solution.
-
Introducing Inequalities: Instead of an equals sign, we could use inequality symbols (<, >, ≤, ≥). This introduces the concept of solving inequalities, a crucial skill in various mathematical applications. For example, 2x + 1 > 7 would lead to x > 3.
-
More Complex Equations: This simple equation forms a basis for understanding and solving more complex equations involving multiple variables, exponents, and other mathematical functions.
Philosophical Reflections: Truth and Mathematical Certainty
While seemingly trivial, the equation 2x + 1 = 7 offers a glimpse into the nature of mathematical truth. The solution, x = 3, is not a matter of opinion or interpretation; it's a demonstrable fact derived through logical manipulation. This highlights the certainty and objectivity often associated with mathematics. The equation embodies a fundamental aspect of mathematical reasoning: the pursuit of logical consistency and the derivation of certain truths from established axioms and rules.
Frequently Asked Questions (FAQs)
-
Q: What if I subtract 2x from both sides first? A: While it’s not the most common approach, subtracting 2x from both sides is perfectly valid. It leads to 1 = 7 - 2x, then you can solve for x through further manipulation. The result will be the same (x = 3).
-
Q: Can I multiply both sides by a fraction instead of dividing? A: Yes, multiplying both sides by 1/2 is equivalent to dividing by 2. Both methods achieve the same outcome.
-
Q: Are there other ways to solve this equation? A: While the presented method is straightforward and efficient, other valid algebraic manipulations could lead to the same solution.
-
Q: What if the equation was 2x + 1 = 8? A: Following the same steps, you would find x = 3.5 or 7/2.
Conclusion: A Foundation for Future Learning
The seemingly simple equation 2x + 1 = 7 provides a powerful foundation for understanding fundamental concepts in algebra and problem-solving. Its solution, x = 3, is not just a numerical answer; it represents a gateway to exploring broader mathematical principles and developing crucial analytical skills. From understanding inverse operations and properties of equality to appreciating the nature of mathematical truth, this simple equation offers a surprisingly rich learning experience. Its value extends beyond rote memorization; it encourages critical thinking, logical reasoning, and a deeper appreciation for the elegance and power of mathematics. By mastering this fundamental equation, students lay a strong groundwork for tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
20 Of 575
Sep 23, 2025
-
32 3 4
Sep 23, 2025
-
48 3kg In Stone
Sep 23, 2025
-
17 8kg In Stone
Sep 23, 2025
-
82 2kg In Stones
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2x 1 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.