27 X 9
interactiveleap
Sep 17, 2025 · 6 min read
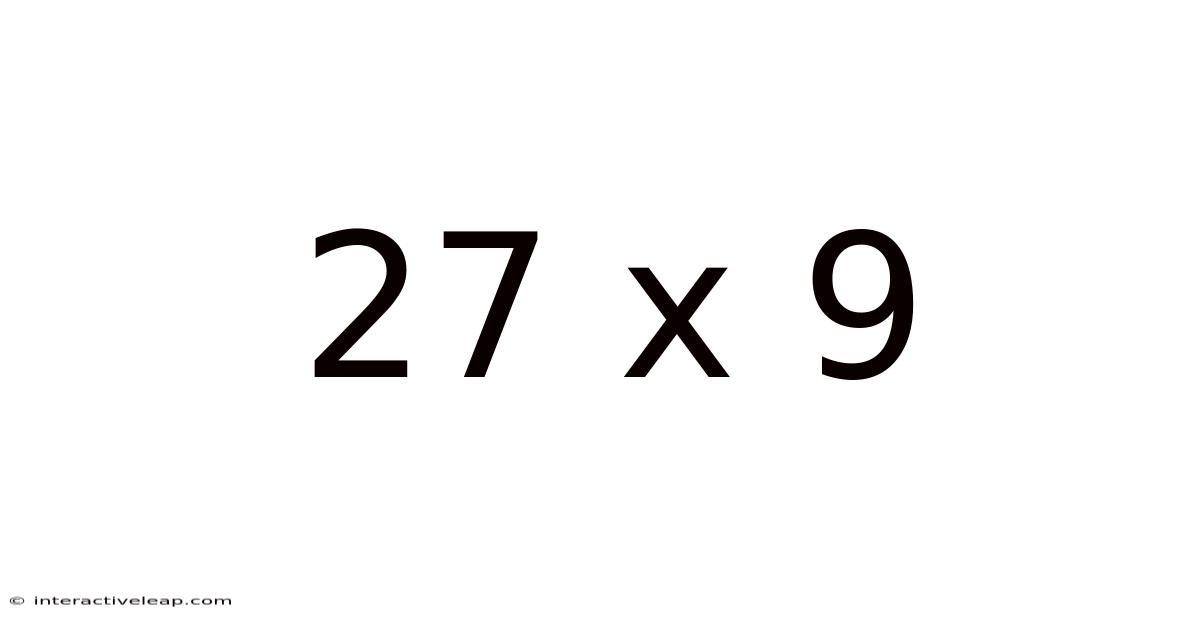
Table of Contents
Unpacking the Mystery: A Deep Dive into 27 x 9
The seemingly simple multiplication problem, 27 x 9, offers a surprisingly rich landscape for exploration. This seemingly straightforward calculation opens doors to understanding fundamental mathematical concepts, exploring different calculation methods, and even appreciating the elegant patterns hidden within numbers. This article will delve into the intricacies of 27 x 9, offering multiple approaches to solving the problem and highlighting the broader mathematical principles involved. We'll move beyond a simple answer and uncover the beauty and logic inherent in this seemingly basic arithmetic operation.
I. The Direct Approach: Standard Multiplication
The most straightforward method for solving 27 x 9 is through standard long multiplication. This method, taught in elementary schools worldwide, provides a systematic approach to multiplying multi-digit numbers.
-
Step 1: Set up the problem: Write 27 above 9, aligning the digits vertically.
-
Step 2: Multiply the ones digit: 9 multiplied by 7 (the ones digit of 27) equals 63. Write down the 3 and carry-over the 6.
-
Step 3: Multiply the tens digit: 9 multiplied by 2 (the tens digit of 27) equals 18. Add the carry-over 6 to get 24.
-
Step 4: Combine the results: The final answer is 243.
Therefore, 27 x 9 = 243. This method is reliable and foundational, providing a solid base for understanding more complex multiplications.
II. Alternative Methods: Exploring Different Approaches
While standard multiplication is efficient, exploring alternative methods enhances understanding and reveals the interconnectedness of mathematical concepts.
A. Distributive Property
The distributive property states that a(b + c) = ab + ac. We can apply this to 27 x 9 by breaking down 27:
27 x 9 = (20 + 7) x 9 = (20 x 9) + (7 x 9) = 180 + 63 = 243
This method demonstrates a deeper understanding of how multiplication works, showcasing its relationship with addition. It's particularly useful for mental calculations, allowing for easier manipulation of smaller numbers.
B. Breaking Down the Multiplier
Instead of breaking down the multiplicand (27), we can break down the multiplier (9):
27 x 9 = 27 x (10 - 1) = (27 x 10) - (27 x 1) = 270 - 27 = 243
This method leverages the ease of multiplying by 10, a common shortcut in mental arithmetic. It showcases the power of subtraction in conjunction with multiplication.
C. Using the Lattice Method
The lattice method, a visually appealing alternative, involves creating a grid. This method is especially helpful for visualizing the process of multiplication and is often preferred by visual learners.
-
Step 1: Create a grid: Draw a 2x2 grid, dividing each square diagonally.
-
Step 2: Place the numbers: Write 27 above the grid and 9 to the right.
-
Step 3: Multiply and place digits: Multiply each digit of 27 by 9 individually. Place the tens digit above the diagonal and the ones digit below. For example, 2 x 9 = 18, so place 1 above and 8 below in the top left square. 7 x 9 = 63, so place 6 above and 3 below in the bottom right square.
-
Step 4: Add diagonally: Add the numbers along the diagonals, starting from the bottom right. This will give you the final answer.
The lattice method, while slightly more time-consuming initially, offers a strong visual representation of the multiplication process and can be beneficial for understanding the place value of numbers.
III. Exploring Patterns and Number Properties
Mathematics is rife with fascinating patterns. Examining 27 x 9 reveals some interesting connections:
A. The Nine Times Table
Observing the nine times table reveals a pattern:
- 9 x 1 = 9
- 9 x 2 = 18
- 9 x 3 = 27
- 9 x 4 = 36
- 9 x 5 = 45
- 9 x 6 = 54
- 9 x 7 = 63
- 9 x 8 = 72
- 9 x 9 = 81
- 9 x 10 = 90
Notice that the sum of the digits in each product always adds up to 9 (or a multiple of 9). For example, in 27 x 9 = 243, 2 + 4 + 3 = 9. This pattern is a consequence of the divisibility rule for 9.
B. Divisibility Rules
The number 243 is divisible by 3 and 9 because the sum of its digits is divisible by 3 and 9. This highlights the relationship between divisibility rules and the properties of numbers. Understanding divisibility rules allows for quick checks of factors and simplifies calculations.
C. Factors and Multiples
27 and 9 share a common factor of 3 and 9. This can be seen in the prime factorization of both numbers: 27 = 3 x 3 x 3 and 9 = 3 x 3. Understanding factors and multiples is crucial in simplifying fractions and solving algebraic equations.
IV. Applications in Real-World Scenarios
While seemingly abstract, the principles involved in calculating 27 x 9 have numerous practical applications:
- Shopping: Calculating the total cost of 9 items priced at $27 each.
- Measurement: Determining the area of a rectangle with sides of 27 units and 9 units.
- Construction: Calculating the number of bricks needed for a wall with 27 rows and 9 bricks per row.
- Programming: Multiplication is a fundamental operation in programming and is used in countless applications.
V. Frequently Asked Questions (FAQs)
Q: What is the easiest way to multiply 27 by 9?
A: The easiest method depends on individual preference and mathematical skills. For some, standard multiplication is the most efficient. Others might find the distributive property or breaking down the multiplier easier. Experiment with different methods to find what works best for you.
Q: Why is the sum of the digits in 243 equal to 9?
A: This is due to the divisibility rule for 9. A number is divisible by 9 if the sum of its digits is divisible by 9.
Q: Are there any other interesting patterns related to 27 and 9?
A: Yes, exploring the multiples of 27 and 9 reveals further patterns and relationships. For example, the difference between consecutive multiples of 9 increases consistently by 9.
Q: Can this be solved using a calculator?
A: Yes, a calculator provides a quick and efficient solution. However, understanding the underlying mathematical principles is crucial for broader mathematical comprehension.
VI. Conclusion
The seemingly simple equation, 27 x 9, opens a window into the rich world of mathematics. Beyond the straightforward answer of 243, this problem offers opportunities to explore various calculation methods, appreciate the beauty of patterns and number properties, and understand the practical applications of fundamental arithmetic operations. By approaching this problem from multiple perspectives, we deepen our understanding of numbers, operations, and the elegance inherent in mathematical principles. The journey of understanding 27 x 9 is not just about arriving at the answer; it’s about appreciating the journey itself and the mathematical landscape it unveils. This comprehensive exploration serves as a testament to the power of simple arithmetic and its far-reaching implications. It encourages readers to look beyond the surface of mathematical problems and discover the richness and interconnectedness within.
Latest Posts
Related Post
Thank you for visiting our website which covers about 27 X 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.