25 Of 9
interactiveleap
Sep 21, 2025 · 6 min read
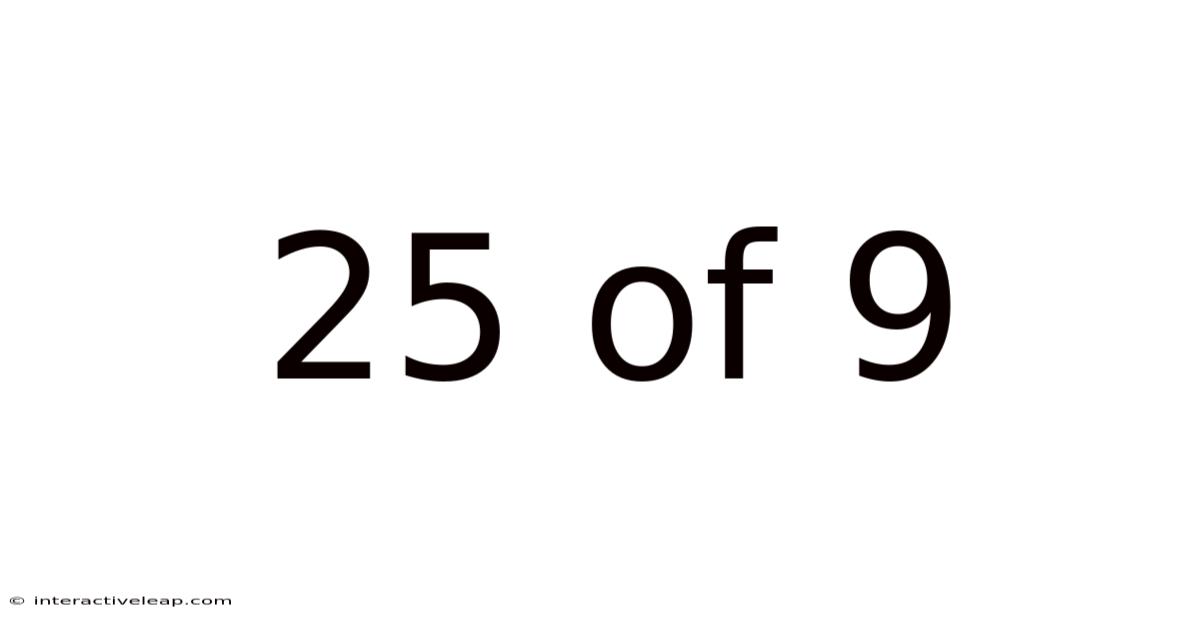
Table of Contents
Decoding the Enigma: 25 of 9 and the Power of Mathematical Ratios
The seemingly simple fraction, 25/9, holds a surprising depth and significance beyond its basic arithmetic value. Understanding this ratio unlocks insights into various fields, from music theory and the golden ratio to practical applications in engineering and design. This article delves into the multifaceted nature of 25/9, exploring its mathematical properties, real-world applications, and connections to other intriguing mathematical concepts. We'll unravel the mystery behind this seemingly ordinary fraction, revealing its hidden beauty and power.
Understanding the Basics: 25/9 as a Fraction and Decimal
At its core, 25/9 is simply a fraction – a representation of a part of a whole. To understand it better, we can convert it into a decimal: 25 divided by 9 equals approximately 2.777... The repeating decimal '.777...' indicates that this is a rational number – a number that can be expressed as a fraction of two integers. This seemingly simple conversion already lays the groundwork for understanding its potential significance in various contexts.
The Mathematical Properties of 25/9
Beyond its basic representation, 25/9 possesses interesting mathematical properties. Let's explore some of them:
-
Irrationality and Rationality: While the decimal representation of 25/9 appears irrational due to the repeating decimal, it is fundamentally a rational number because it can be expressed as a precise fraction. This distinction highlights the subtle differences between decimal representation and the actual mathematical nature of a number.
-
Relationship to other fractions: 25/9 can be simplified by finding common factors between the numerator and the denominator. However, in this case, 25 and 9 share no common factors other than 1, meaning the fraction is already in its simplest form. Its relationship to other fractions might be explored through comparisons and relative magnitudes. For instance, we can compare it to fractions like 3/1 (3) or 2/1 (2), highlighting its position within the number line.
-
Approximation of other numbers: 25/9 provides a relatively close approximation to certain irrational numbers. This property can be useful in estimations and practical applications where perfect accuracy isn't always required. The closeness of this approximation to other mathematical constants will be explored further in the following sections.
25/9 in Music Theory and the Golden Ratio
The ratio 25/9 exhibits intriguing links to musical theory and the famed golden ratio (approximately 1.618). While not a direct manifestation of the golden ratio, its proximity to other ratios associated with harmonic intervals in music suggests a potential connection. Let's investigate this further:
-
Musical Intervals: In music, intervals are defined by the ratio of frequencies between two notes. Certain ratios, like 3/2 (perfect fifth) and 4/3 (perfect fourth), create consonant and harmonious sounds. Although 25/9 doesn't directly correspond to a standard musical interval, its proximity to certain ratios could potentially influence the perception of musical harmony in specific contexts. Further research into microtonal music and alternative tuning systems might reveal more about its role.
-
Connection to the Golden Ratio: The golden ratio (φ) is found extensively in nature and art, often associated with aesthetic harmony and balance. While 25/9 is not directly equal to φ, its numerical proximity to ratios related to Fibonacci sequence (which is intrinsically linked to the golden ratio) might suggest an indirect connection. Exploring the relationship between the Fibonacci sequence and 25/9 might unveil subtle but meaningful connections.
Practical Applications of the 25/9 Ratio
While not as widely recognized as other mathematical constants, the ratio 25/9 finds practical application in specific engineering and design scenarios:
-
Gear Ratios: In mechanical engineering, gear ratios are used to transfer power between rotating shafts. A gear ratio of 25/9 could be employed in specific applications requiring a precise speed reduction or torque amplification. The specific applications would depend on the desired outcome and the overall mechanical design.
-
Scale Models: In architecture and model making, 25/9 could be used as a scale factor to create a smaller representation of a larger structure. This scale would need to be carefully considered to ensure accurate representation and maintain the proportions of the original object.
-
Aspect Ratios: In graphic design and video production, aspect ratios define the proportional relationship between the width and height of an image or screen. While not a standard aspect ratio, 25/9 could be utilized in specialized applications where a non-standard proportion is needed for a specific artistic or technical effect.
Further Exploration: Unveiling the Hidden Depths
The exploration of 25/9 doesn't end here. There are several avenues for further investigation:
-
Continued Fractions: Representing 25/9 as a continued fraction might reveal hidden patterns and relationships with other mathematical structures. Continued fractions provide a different way to represent rational and irrational numbers, and could offer new perspectives on the properties of 25/9.
-
Number Theory: Delving into number theory might uncover deeper mathematical properties related to the prime factorization of 25 and 9. This could reveal connections to other areas of mathematics and provide a more comprehensive understanding of the underlying structure of the ratio.
-
Computational Analysis: Employing computational methods could help explore the behavior of 25/9 in complex systems and models. This approach could lead to the discovery of unexpected applications and reveal the role of this ratio in various mathematical and scientific domains.
Frequently Asked Questions (FAQs)
Q: Is 25/9 a rational or irrational number?
A: 25/9 is a rational number because it can be expressed as a fraction of two integers. While its decimal representation is a repeating decimal (2.777...), this doesn't change its rational nature.
Q: What are some real-world applications of 25/9?
A: 25/9 finds application in gear ratios in mechanical engineering, scale models in architecture and design, and potentially in specific aspect ratios in graphic design.
Q: How is 25/9 related to the golden ratio?
A: While not directly equal to the golden ratio, 25/9's proximity to ratios related to the Fibonacci sequence suggests a possible indirect connection, warranting further investigation.
Q: Can 25/9 be simplified?
A: No, 25/9 is already in its simplest form as 25 and 9 share no common factors other than 1.
Conclusion: The Enduring Significance of 25/9
While initially appearing as a simple fraction, 25/9 reveals its significance through deeper mathematical exploration and its surprising connections to various fields. From its potential role in music theory and the subtle links to the golden ratio, to its practical applications in engineering and design, 25/9 showcases the richness and interconnectedness of mathematical concepts. This article has only scratched the surface of its potential. Further research and exploration are encouraged to uncover the hidden depths and enduring significance of this seemingly ordinary ratio. The beauty of mathematics lies in its capacity to reveal hidden connections and unlock unexpected insights – and 25/9 serves as a perfect illustration of this principle. Its simplicity belies a complexity that invites further investigation and discovery, making it a fascinating subject for mathematical exploration.
Latest Posts
Latest Posts
-
Stack Of Pancakes
Sep 21, 2025
-
Mark Henry Leg
Sep 21, 2025
-
33km To Miles
Sep 21, 2025
-
Mg Versus Ml
Sep 21, 2025
-
4th Lateran Council
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.