25 Of 45
interactiveleap
Sep 15, 2025 · 5 min read
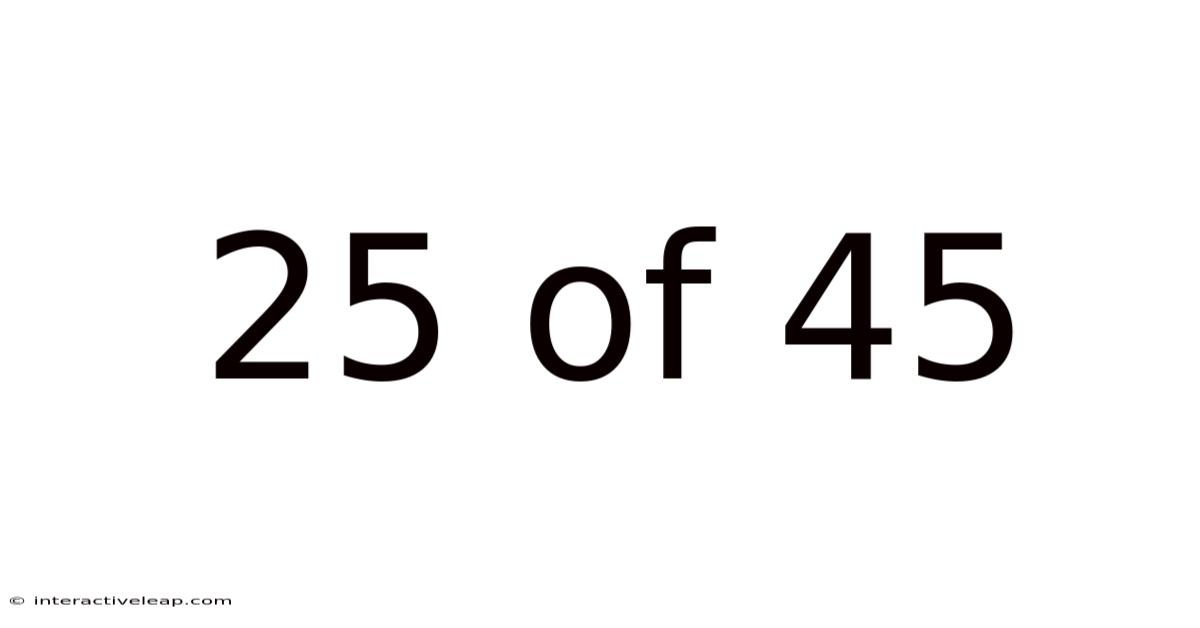
Table of Contents
Decoding the Fraction: Understanding 25 out of 45
This article delves into the meaning and implications of the fraction 25/45, exploring its simplification, percentage representation, and practical applications. We'll unpack the concept in a clear and accessible manner, providing a comprehensive understanding for students, educators, and anyone curious about the world of fractions and percentages. Understanding fractions like 25/45 is crucial for everyday life, from calculating discounts to understanding statistical data.
Understanding the Fraction 25/45
The fraction 25/45 represents a part-to-whole relationship. It indicates that we have 25 parts out of a total of 45 parts. This fraction can be visualized as 25 pieces of a pizza that's been divided into 45 equal slices. Understanding this fundamental concept is the first step in mastering fractions.
Simplifying the Fraction
One of the core principles of working with fractions is simplification. Simplifying a fraction means reducing it to its lowest terms, while maintaining its value. To simplify 25/45, we need to find the greatest common divisor (GCD) of both the numerator (25) and the denominator (45). The GCD is the largest number that divides both numbers without leaving a remainder.
The factors of 25 are 1, 5, and 25. The factors of 45 are 1, 3, 5, 9, 15, and 45.
The greatest common factor of 25 and 45 is 5. We divide both the numerator and the denominator by 5:
25 ÷ 5 = 5 45 ÷ 5 = 9
Therefore, the simplified form of 25/45 is 5/9. This simplified fraction retains the same value as the original fraction, but it's expressed in a more concise and manageable form.
Converting to Percentage
Converting a fraction to a percentage is a common task with many practical applications. To convert 25/45 (or its simplified form, 5/9) to a percentage, we follow these steps:
-
Divide the numerator by the denominator: 5 ÷ 9 ≈ 0.5556
-
Multiply the result by 100: 0.5556 × 100 ≈ 55.56
Therefore, 25/45 is approximately 55.56%. This percentage represents the proportion of 25 out of 45 as a value out of 100.
Real-World Applications of 25/45 and its Equivalent, 5/9
The fraction 25/45, and its simplified version 5/9, appears in various real-world scenarios. Understanding its value can help you solve problems in various fields:
-
Statistics and Probability: Imagine a survey where 25 out of 45 respondents answered "yes" to a particular question. The fraction 25/45 (or 5/9) represents the proportion of "yes" responses, enabling you to analyze the results and draw conclusions.
-
Sales and Discounts: If a store offers a discount of 25/45 (or 5/9) off the original price, you can use this fraction to calculate the discount amount and the final price.
-
Recipe Scaling: If a recipe calls for 25 grams of ingredient A for a total of 45 servings, you can use this fraction to adjust the recipe for a smaller or larger number of servings.
-
Measurement and Proportion: In various fields, such as engineering and construction, understanding proportions and ratios, which 25/45 represents, is essential for accurate calculations and measurements.
-
Data Analysis: When working with datasets, the fraction 25/45 might represent the proportion of data points with a certain characteristic. Understanding this fraction is key to interpreting the data and identifying trends.
Further Exploration: Fractions, Decimals, and Percentages
The relationship between fractions, decimals, and percentages is fundamental to mathematical understanding. We've already seen how to convert a fraction (25/45) to a percentage (55.56%). Let's explore the connection further:
-
Fraction to Decimal: To convert a fraction to a decimal, simply divide the numerator by the denominator. For example, 5/9 ≈ 0.5556.
-
Decimal to Percentage: To convert a decimal to a percentage, multiply by 100. For example, 0.5556 × 100 = 55.56%.
-
Percentage to Fraction: To convert a percentage to a fraction, divide by 100 and simplify. For example, 55.56% = 55.56/100 = 5556/10000. This fraction can be further simplified by dividing both numerator and denominator by their GCD (which is 4). The result is 1389/2500.
Practical Exercises
To solidify your understanding, try these exercises:
-
Simplify the following fractions: 15/45, 30/60, 10/25
-
Convert the following fractions to percentages: 1/4, 2/5, 3/8
-
A survey showed that 15 out of 35 students prefer apples over oranges. What percentage of students prefer apples?
-
A store offers a 20% discount on an item originally priced at $50. What is the final price?
-
A recipe calls for 25ml of milk for every 45g of flour. How much milk is needed if you use 90g of flour?
Frequently Asked Questions (FAQ)
-
Q: What is the difference between a proper fraction and an improper fraction?
-
A: A proper fraction has a numerator smaller than the denominator (e.g., 5/9). An improper fraction has a numerator equal to or greater than the denominator (e.g., 9/5).
-
Q: How do I add or subtract fractions?
-
A: To add or subtract fractions, they must have the same denominator. If they don't, find a common denominator, then add or subtract the numerators. Keep the denominator the same.
-
Q: How do I multiply fractions?
-
A: Multiply the numerators together, and multiply the denominators together. Simplify the resulting fraction if possible.
-
Q: How do I divide fractions?
-
A: To divide fractions, invert the second fraction (reciprocal) and multiply.
Conclusion
Understanding fractions, like 25/45, is a fundamental skill applicable across various aspects of life. Through simplification, percentage conversion, and the exploration of real-world applications, we’ve uncovered the practical significance of this seemingly simple fraction. By mastering these concepts, you equip yourself with powerful tools for problem-solving and critical thinking across numerous disciplines. Remember to practice regularly and apply these concepts in your daily life to strengthen your understanding. The more you engage with fractions, the more comfortable and confident you will become in working with them.
Latest Posts
Latest Posts
-
80g To Ounces
Sep 15, 2025
-
2000mm In Metres
Sep 15, 2025
-
Magnesium Sulfide Formula
Sep 15, 2025
-
225lbs In Kg
Sep 15, 2025
-
130 Kmh Mph
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.