25 Of 4
interactiveleap
Sep 17, 2025 · 6 min read
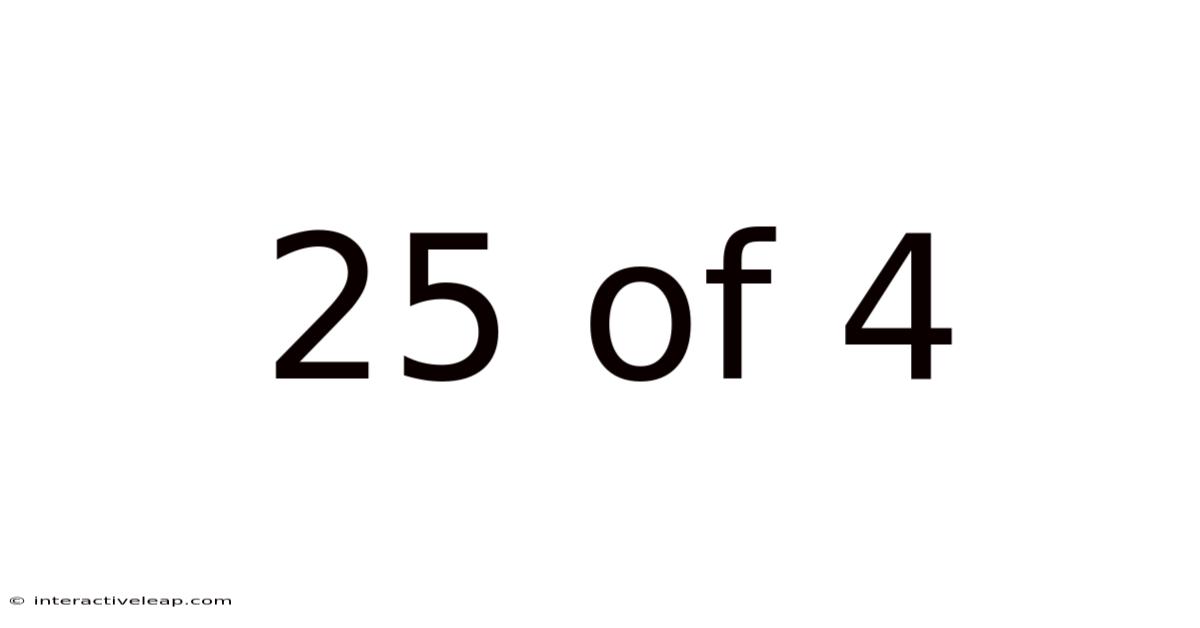
Table of Contents
Unveiling the Mystery of 25/4: A Deep Dive into Fraction Division
Understanding fractions can feel like navigating a maze, especially when division enters the picture. This comprehensive guide will illuminate the seemingly complex world of dividing fractions, focusing specifically on the problem 25/4, and providing you with the tools to tackle any similar fraction division problem with confidence. We'll explore various methods, delve into the underlying mathematical principles, and address frequently asked questions, ensuring you leave with a thorough understanding not just of this specific problem, but of the broader concept.
Introduction: Decoding Fraction Division
The expression "25/4" represents a fraction where 25 is the numerator (the top number) and 4 is the denominator (the bottom number). Dividing fractions might seem daunting, but it's a surprisingly straightforward process once you grasp the fundamental principles. This article will demystify the process, teaching you not just how to calculate 25/4, but also the why behind the steps, empowering you to tackle any fraction division problem independently. We’ll cover multiple approaches, making sure you find the method that best suits your learning style.
Method 1: Converting to an Improper Fraction
The most common approach to solving 25/4 involves converting it into an improper fraction (where the numerator is larger than the denominator) and then simplifying. Since 25 is already larger than 4, we don't need to convert a mixed number. The fraction 25/4 is already an improper fraction and ready to be further evaluated.
Let’s visualize this: Imagine you have 25 identical items, and you want to divide them equally among 4 groups. How many items will each group receive? This is precisely what 25/4 represents.
To calculate this, we perform the division: 25 ÷ 4 = 6 with a remainder of 1.
This can be expressed as a mixed number: 6 remainder 1 or 6 ¹/₄. Therefore, 25/4 is equal to 6 ¼. This means each of the 4 groups receives 6 whole items, and there's 1 item left over, which is represented by the fraction ¹/₄.
Method 2: Long Division
Long division provides a step-by-step approach to solving 25/4. Here's how it works:
-
Set up the problem: Write 25 inside the long division symbol (÷) and 4 outside.
-
Divide: How many times does 4 go into 25? It goes in 6 times (4 x 6 = 24).
-
Subtract: Subtract 24 from 25, leaving a remainder of 1.
-
Express the remainder: The remainder of 1 becomes the numerator of a fraction, and the divisor (4) remains the denominator. This gives us ¹/₄.
-
Combine: Combine the whole number (6) and the fraction (¹/₄) to get the final answer: 6 ¼.
This method reinforces the concept of dividing and handling the remainder, providing a concrete visualization of the division process.
Method 3: Decimal Conversion
Another approach involves converting the fraction into its decimal equivalent. To do this, we simply divide the numerator by the denominator:
25 ÷ 4 = 6.25
This decimal representation (6.25) is another way to express the result of dividing 25 by 4. It's particularly useful when dealing with calculations that require decimal values. Understanding this equivalence is crucial for converting between fractions and decimals, a vital skill in various mathematical applications.
Method 4: Understanding the Concept of Ratios and Proportions
Viewing 25/4 through the lens of ratios and proportions offers another layer of understanding. The fraction represents a ratio of 25 to 4, indicating the relationship between these two quantities. You can interpret this as 25 parts out of a total of 4 parts, which, through division, simplifies to the equivalence we've already established. This perspective highlights the proportional relationship between the numerator and denominator.
The Importance of Simplifying Fractions
Regardless of the method employed, simplifying the resulting fraction to its lowest terms is crucial. In this case, 6 ¹/₄ is already in its simplest form because the numerator (1) and denominator (4) share no common factors other than 1. However, in other fraction division problems, you might need to simplify the resulting fraction to obtain the most concise representation. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Explaining the Math Behind Fraction Division
The fundamental principle behind dividing fractions is the concept of reciprocals. To divide by a fraction, we multiply by its reciprocal. The reciprocal of a fraction is obtained by simply swapping the numerator and the denominator.
For instance, the reciprocal of 4 (which can be written as 4/1) is 1/4. Therefore, dividing 25 by 4 is the same as multiplying 25 by 1/4:
25 × (1/4) = 25/4 = 6.25 or 6 ¹/₄
This fundamental concept underlies all fraction division problems and highlights the interconnectedness of different mathematical operations.
Frequently Asked Questions (FAQ)
- Q: Why are there multiple ways to solve 25/4?
A: Different methods cater to different learning styles and mathematical preferences. Some find long division intuitive, while others prefer the visual representation of converting to a mixed number. The choice of method depends entirely on individual preference and the context of the problem.
- Q: What if the numerator wasn't larger than the denominator?
A: If the numerator were smaller than the denominator, the result would be a proper fraction (a fraction less than 1). The same methods apply, but the answer would be a fraction instead of a mixed number or a whole number with a decimal component.
- Q: Can I use a calculator to solve this?
A: Yes, calculators can efficiently handle fraction division. However, understanding the underlying mathematical principles is crucial for problem-solving beyond simple calculations. Calculators are tools to assist, not replace, understanding.
- Q: What are some real-world applications of fraction division?
A: Fraction division appears frequently in everyday life, from dividing recipes to calculating material needs for construction projects. It's a fundamental skill applicable across various fields.
Conclusion: Mastering Fraction Division
Mastering fraction division, exemplified by solving 25/4, is a cornerstone of mathematical proficiency. By understanding the various methods, from long division to converting to mixed numbers and decimals, you've equipped yourself with the knowledge to tackle a wide range of fraction-based problems. Remember that the key lies not only in obtaining the correct answer but also in understanding the why behind the process. This deeper comprehension will pave the way for tackling more complex mathematical challenges with confidence and ease. The seemingly complex world of fractions becomes much more manageable when approached systematically and with a thorough understanding of the underlying principles. So, embrace the challenge, practice regularly, and watch your mathematical abilities flourish!
Latest Posts
Latest Posts
-
C Est Magnifique Translation
Sep 17, 2025
-
80 Of 56
Sep 17, 2025
-
6 9kg In Lbs
Sep 17, 2025
-
25 M Square
Sep 17, 2025
-
Deana Lawson Photography
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.