25 Of 145
interactiveleap
Sep 16, 2025 · 5 min read
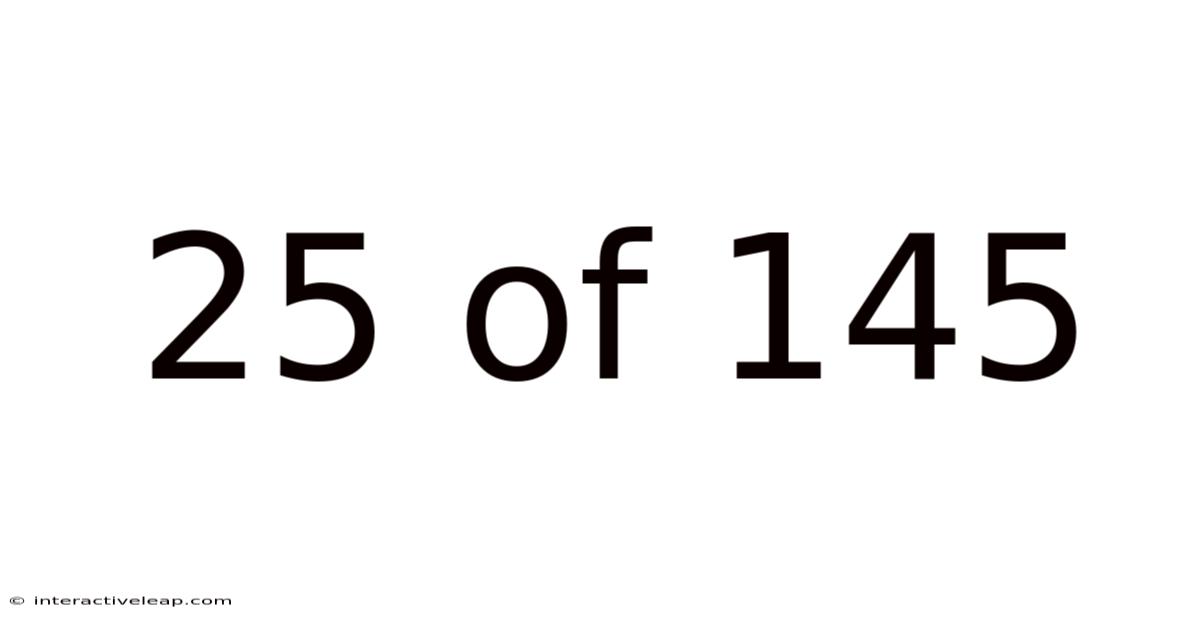
Table of Contents
Decoding the Enigma: Understanding the Fraction 25/145 and its Implications
The seemingly simple fraction 25/145 might appear insignificant at first glance. However, exploring this fraction opens doors to a deeper understanding of fundamental mathematical concepts like simplification, ratios, percentages, and their applications in real-world scenarios. This article will delve into the intricacies of 25/145, unraveling its hidden meanings and showcasing its practical relevance. We will cover simplification techniques, conversion to decimals and percentages, explore its implications in various contexts, and address frequently asked questions.
Simplifying the Fraction: Unveiling the Core
The first step in understanding 25/145 is to simplify it to its lowest terms. Simplification involves finding the greatest common divisor (GCD) of the numerator (25) and the denominator (145) and dividing both by this GCD.
Let's find the GCD of 25 and 145. We can use the Euclidean algorithm or prime factorization.
-
Prime Factorization: 25 = 5 x 5 and 145 = 5 x 29. The common factor is 5.
-
Euclidean Algorithm:
- 145 ÷ 25 = 5 with a remainder of 20
- 25 ÷ 20 = 1 with a remainder of 5
- 20 ÷ 5 = 4 with a remainder of 0
The GCD is 5. Therefore, we divide both the numerator and the denominator by 5:
25 ÷ 5 = 5 145 ÷ 5 = 29
Thus, the simplified fraction is 5/29. This simplified form represents the same value as 25/145 but is more concise and easier to work with.
Converting to Decimal and Percentage: Expanding the Representation
While the fractional form (5/29) is precise, converting it to decimal and percentage forms offers alternative perspectives and facilitates easier comparisons.
To convert 5/29 to a decimal, we perform the division:
5 ÷ 29 ≈ 0.1724
To convert the decimal to a percentage, we multiply by 100:
0.1724 x 100 ≈ 17.24%
Therefore, 25/145, simplified to 5/29, is approximately 0.1724 or 17.24%. This percentage representation allows for quick comparisons and interpretations within various contexts.
Real-World Applications: Contextualizing the Fraction
The fraction 25/145, or its simplified form 5/29, can represent various real-world scenarios. Consider these examples:
-
Test Scores: Imagine a student scoring 25 out of 145 points on a test. Their score, simplified to 5/29 or approximately 17.24%, indicates a relatively low performance. This information allows for better understanding of the student's performance and areas requiring improvement.
-
Survey Results: Suppose a survey of 145 people reveals that 25 prefer a particular product. The fraction 5/29 (or 17.24%) represents the proportion of respondents who prefer that product. This data is crucial for market research and product development.
-
Financial Ratios: In finance, ratios are extensively used to analyze the financial health of a company. A ratio of 25/145 could represent a specific financial metric, such as the ratio of current assets to total assets. Simplifying this ratio to 5/29 provides a clearer understanding of the company's financial position.
-
Probabilities: In probability theory, fractions are used to express the likelihood of an event. For example, if there are 145 equally likely outcomes, and 25 of them represent a specific event, the probability of that event occurring is 5/29, or approximately 17.24%.
Further Mathematical Explorations: Expanding the Scope
The fraction 25/145 offers opportunities to explore several mathematical concepts beyond simple simplification and conversion:
-
Ratios and Proportions: The fraction represents a ratio of 25 to 145. This ratio can be used to solve problems involving proportions. For instance, if a larger sample of 290 people were surveyed, we could proportionally predict that approximately 100 (5/29 * 290) would prefer the same product.
-
Equivalent Fractions: Understanding that 25/145 is equivalent to 5/29 highlights the concept of equivalent fractions. This understanding is crucial for working with fractions in more complex mathematical operations.
-
Fraction Operations: The fraction can be used to practice adding, subtracting, multiplying, and dividing fractions. These operations build a solid foundation for advanced mathematical concepts.
Frequently Asked Questions (FAQ)
Q1: Why is simplification important?
A1: Simplification makes fractions easier to understand and work with. The simplified form (5/29) is more concise and allows for quicker calculations and comparisons.
Q2: Are there other methods to find the GCD?
A2: Yes, besides prime factorization and the Euclidean algorithm, other methods include the listing method (listing all the factors of both numbers) and the ladder method (repeatedly dividing both numbers by common factors).
Q3: How accurate is the decimal approximation?
A3: The accuracy of the decimal approximation (0.1724) depends on the number of decimal places used. More decimal places provide a more accurate representation.
Q4: Can this fraction be expressed as a recurring decimal?
A4: No, the fraction 5/29 does not result in a recurring decimal. The decimal representation will eventually terminate.
Conclusion: Beyond the Numbers
While initially appearing simple, the fraction 25/145 offers a rich learning experience. Through simplification, conversion to decimals and percentages, and exploration of its real-world applications, we gain a deeper understanding of fundamental mathematical concepts. This seemingly insignificant fraction highlights the power of mathematics in providing a framework for understanding and interpreting our world. The ability to simplify, analyze, and contextualize such fractions equips us with essential problem-solving skills applicable in various fields. From interpreting test scores to analyzing financial data, the fraction 25/145 serves as a microcosm of the broader relevance and significance of mathematical literacy. Therefore, understanding its implications is far more valuable than simply calculating its simplified form. It's a gateway to a deeper appreciation of the interconnectedness of numbers and their relevance to our lives.
Latest Posts
Latest Posts
-
Boat In Pond
Sep 16, 2025
-
65 30 Off
Sep 16, 2025
-
290kpa To Psi
Sep 16, 2025
-
39 3 Celsius Fahrenheit
Sep 16, 2025
-
7 6kg To Lbs
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 145 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.