25 Of 11000
interactiveleap
Sep 22, 2025 · 6 min read
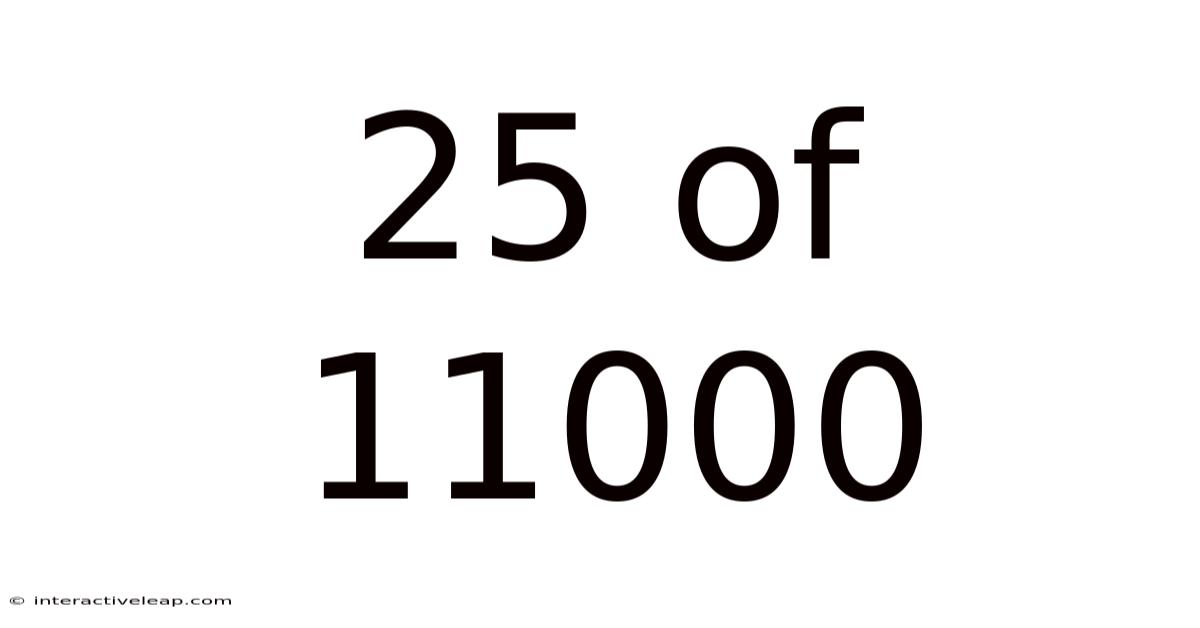
Table of Contents
Unveiling the Significance of 25 out of 11000: A Deep Dive into Percentages, Probability, and Statistical Significance
This article explores the seemingly small fraction of 25 out of 11000, delving into its implications in various contexts. We'll examine how to express this ratio as a percentage, analyze its probabilistic significance, and discuss its interpretation within the broader framework of statistical analysis. Understanding the implications of such a ratio is crucial across diverse fields, from scientific research and market analysis to risk assessment and quality control. We’ll uncover how a seemingly insignificant number can hold significant weight depending on the situation.
Calculating the Percentage: A Simple Approach
The first step in understanding the significance of 25 out of 11000 is converting it into a percentage. This allows for easier comparison with other ratios and facilitates a clearer understanding of its relative size. The calculation is straightforward:
(25 / 11000) x 100% = 0.227% (approximately)
This tells us that 25 represents approximately 0.227% of 11000. While this percentage seems small, its interpretation hinges heavily on the context in which it appears.
Probabilistic Interpretation: What Does it Mean?
The interpretation of 25 out of 11000 significantly depends on the underlying probability distribution. Let's consider several scenarios:
-
Scenario 1: Random Sampling: If this ratio represents a random sample from a larger population, then we can explore the probability of observing such a result. We might use techniques like binomial probability or hypothesis testing to assess if this observed frequency is significantly different from what we might expect by chance alone. For instance, if we’re analyzing the prevalence of a specific gene mutation, we would need more information to determine if 25 occurrences in a sample of 11000 is statistically significant.
-
Scenario 2: Defect Rate in Manufacturing: In quality control, 25 defects out of 11000 products might represent a significant issue. Even though it's a small percentage, it indicates a defect rate of approximately 0.23%. Depending on the cost of defects, the safety implications, and the industry standards, this might be unacceptable and require immediate attention to improve the manufacturing process.
-
Scenario 3: Clinical Trial Results: Imagine 25 patients out of 11000 in a clinical trial experienced a specific side effect. While the percentage is low, the absolute number of 25 patients experiencing the side effect is important. The severity of the side effect is also a key factor. A serious side effect in even a small percentage of patients could lead to the cessation of the trial or a reevaluation of the treatment's risk-benefit profile.
Statistical Significance: The Role of Hypothesis Testing
Determining statistical significance requires a formal hypothesis test. This involves establishing a null hypothesis (e.g., there is no difference between the observed ratio and an expected ratio) and an alternative hypothesis (e.g., the observed ratio is significantly different from the expected ratio). We would then use statistical tests (like a chi-squared test or z-test) to determine the probability of observing the data (25 out of 11000) given that the null hypothesis is true. If this probability (the p-value) falls below a predetermined significance level (commonly 0.05), we reject the null hypothesis and conclude that the observed ratio is statistically significant.
The choice of statistical test depends on the nature of the data and the research question. For example, if we are comparing proportions (like comparing the proportion of defects in two different batches of products), a z-test for proportions might be appropriate. If we're analyzing counts (like the number of defects in a single batch), a chi-squared goodness-of-fit test could be used.
Beyond the Numbers: Context is Key
The interpretation of 25 out of 11000 is deeply context-dependent. Several factors influence the significance of this ratio:
-
The Baseline Rate: Comparing the observed ratio to the expected or baseline rate is crucial. If the expected rate is much higher than 0.23%, then the observed rate could be considered low. Conversely, if the expected rate is significantly lower, then the observed rate could be high.
-
The Cost of Errors: The consequences associated with the event represented by the 25 instances play a pivotal role. If the event is a catastrophic failure (e.g., in aerospace engineering), even a small probability is unacceptable. On the other hand, if the event is relatively inconsequential, then the small percentage might not be a concern.
-
Sample Size: The sample size of 11000 is relatively large, which increases the precision of the estimate. However, even with a large sample size, a small percentage may still not be statistically significant if the underlying variability is high.
-
Variability: The inherent variability in the process being studied will impact the interpretation. A high degree of variability might make it difficult to detect a small difference as statistically significant.
Practical Applications: Real-World Examples
Let's illustrate the importance of context with real-world examples:
-
Medical Diagnosis: A 0.23% false-positive rate for a medical test might seem negligible, but if the test is widely used, the absolute number of false positives could be substantial, potentially leading to unnecessary interventions and anxiety.
-
Environmental Monitoring: Detecting 25 cases of a rare pollutant in a water sample of 11000 might indicate a significant environmental concern, warranting further investigation and potential remediation efforts.
-
Financial Risk Assessment: In finance, a 0.23% probability of default on a loan might appear low, but when multiplied by a vast portfolio of loans, the aggregate risk could be substantial.
Frequently Asked Questions (FAQ)
Q: How can I calculate the confidence interval for this ratio?
A: You can calculate a confidence interval for the proportion (0.23%) using the standard formula for confidence intervals for proportions, taking into account the sample size (11000) and the desired confidence level (e.g., 95%). This interval provides a range of plausible values for the true proportion in the population.
Q: What statistical software can I use for further analysis?
A: Many statistical software packages, including R, SPSS, SAS, and Python libraries (like SciPy and Statsmodels), can be used to perform hypothesis testing and calculate confidence intervals for proportions.
Q: What if the sample size was smaller?
A: With a smaller sample size, the precision of the estimate would decrease, making it harder to draw firm conclusions. The same percentage could be statistically insignificant with a smaller sample size, but statistically significant with a larger sample size. This highlights the importance of appropriately designed studies with sufficient sample sizes.
Conclusion: The Importance of Contextual Understanding
The seemingly small ratio of 25 out of 11000 translates to approximately 0.227%. While this might appear insignificant at first glance, its true meaning depends heavily on the context. Understanding the underlying probability distribution, applying appropriate statistical tests to determine statistical significance, and carefully considering the consequences associated with the event represented by the 25 instances are crucial for a meaningful interpretation. This analysis underscores the importance of considering not only the numerical result but also its context to reach informed conclusions and make appropriate decisions. The seemingly simple calculation of a percentage hides a complex interplay of probability, statistics, and practical implications that must be thoroughly examined for a comprehensive understanding.
Latest Posts
Latest Posts
-
Electrostatic Discharge Strap
Sep 22, 2025
-
6 Of 35000
Sep 22, 2025
-
155kmh To Mph
Sep 22, 2025
-
Wire Plastic Coated
Sep 22, 2025
-
125g To Ounces
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 11000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.