25 Of 105
interactiveleap
Sep 23, 2025 · 6 min read
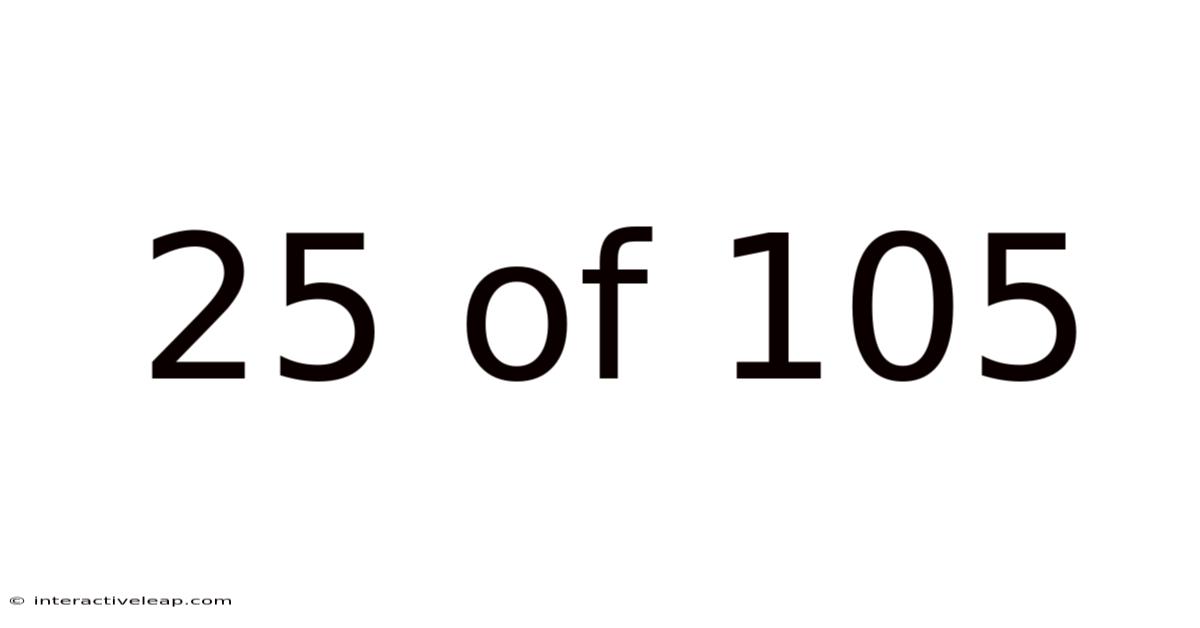
Table of Contents
Unveiling the Mystery: Understanding 25 out of 105 – A Deep Dive into Percentages, Ratios, and Proportions
Understanding fractions, percentages, and ratios is fundamental to many aspects of life, from calculating discounts in a shop to understanding complex scientific data. This article will delve deep into the seemingly simple concept of "25 out of 105," exploring its various representations and applications, and expanding upon the underlying mathematical principles. We will cover how to calculate this ratio, express it as a percentage, simplify it to its lowest terms, and explore its relevance in different contexts. This exploration will provide a solid foundation for anyone looking to improve their understanding of basic mathematics and its practical applications.
What Does "25 out of 105" Mean?
At its core, "25 out of 105" represents a ratio. It indicates a comparison between two quantities – 25 and 105. It can be interpreted as: There are 25 units of something out of a total of 105 units. This could represent anything from 25 correct answers out of 105 questions on a test to 25 red apples out of 105 apples in a basket. The key is the relative proportion of one quantity compared to the whole.
Calculating the Percentage
Converting a ratio to a percentage involves expressing the ratio as a fraction and then multiplying by 100. In this case:
-
Express as a fraction: 25 out of 105 can be written as the fraction 25/105.
-
Simplify the fraction (optional, but recommended): Both 25 and 105 are divisible by 5. Simplifying the fraction gives us 5/21. This simplified fraction represents the same ratio but is easier to work with.
-
Convert to a percentage: To express 5/21 as a percentage, we divide 5 by 21 and then multiply by 100:
(5 ÷ 21) x 100 ≈ 23.81%
Therefore, 25 out of 105 is approximately 23.81%.
Simplifying Ratios to Their Lowest Terms
Simplifying a ratio, as we did above, involves finding the greatest common divisor (GCD) of the two numbers and dividing both by it. The GCD is the largest number that divides both numbers without leaving a remainder. In our example:
- The factors of 25 are 1, 5, and 25.
- The factors of 105 are 1, 3, 5, 7, 15, 21, 35, and 105.
The GCD of 25 and 105 is 5. Dividing both numbers by 5 gives us the simplified ratio 5/21. This simplified form retains the original proportion but makes calculations and comparisons easier.
Real-World Applications of Ratios and Percentages
The concept of "25 out of 105" and its equivalent percentage (approximately 23.81%) has numerous real-world applications across various fields:
-
Education: A student scoring 25 out of 105 on a test would have achieved approximately 23.81%. This percentage can be used to assess their performance relative to the total possible marks.
-
Business and Finance: A company might analyze sales figures, where 25 out of 105 products sold were of a particular type. This ratio can be used to inform inventory management and marketing strategies.
-
Science and Statistics: In scientific experiments, ratios are commonly used to analyze data. For instance, 25 out of 105 participants in a clinical trial might exhibit a specific response to a treatment.
-
Sports: In sports statistics, ratios are ubiquitous. For example, a basketball player might have made 25 shots out of 105 attempts. This ratio is crucial in evaluating a player's shooting accuracy.
-
Everyday Life: From calculating cooking proportions to determining the success rate of a task, understanding ratios and percentages is essential for efficient problem-solving in our daily lives.
Beyond the Basics: Proportions and the Concept of Scale
The ratio 25/105 also exemplifies the principle of proportion. A proportion is a statement that two ratios are equal. For example:
25/105 = 5/21
This indicates that the ratio of 25 to 105 is equivalent to the ratio of 5 to 21. Understanding proportions is crucial for solving problems involving scaling, such as enlarging or reducing images or maps, or adjusting recipes to feed different numbers of people. If a recipe calls for 5 cups of flour and 21 cups of water, maintaining the 5/21 proportion allows you to scale the recipe appropriately, regardless of the number of servings.
Using Ratios and Percentages for Comparative Analysis
Ratios and percentages are powerful tools for comparing different sets of data. Suppose we have two sets of data:
- Set A: 25 out of 105
- Set B: 30 out of 120
While it might be difficult to directly compare 25 out of 105 to 30 out of 120, converting both to percentages provides a clearer picture. Set A is approximately 23.81%, while Set B is 25%. This allows for a simple and direct comparison, indicating that Set B has a slightly higher proportion than Set A.
Exploring Different Representations
The concept of "25 out of 105" can be represented in several ways, each serving a unique purpose:
- Fraction: 25/105 (or its simplified form 5/21)
- Decimal: 0.2381 (approximately)
- Percentage: 23.81% (approximately)
- Ratio: 25:105 (or its simplified form 5:21)
Understanding these different representations allows for flexibility in calculations and communication, enabling the choice of the most suitable form depending on the specific context and purpose.
Addressing Common Misconceptions
Several common misconceptions surround ratios and percentages:
-
Confusing ratios and fractions: While closely related, ratios compare two quantities, while fractions represent a part of a whole. However, a ratio can always be expressed as a fraction.
-
Incorrect simplification: Incorrectly simplifying ratios leads to inaccurate calculations and comparisons. Always ensure you find the greatest common divisor before simplifying.
-
Misinterpreting percentages: Percentages should be interpreted in the context of the total. A 25% increase from a small base value is very different from a 25% increase from a large base value.
Frequently Asked Questions (FAQ)
Q: How can I calculate the percentage without a calculator?
A: For simple percentages, you can use mental math techniques or approximation. For more complex calculations, you can use long division to divide the numerator by the denominator, and then multiply by 100.
Q: What is the difference between a ratio and a proportion?
A: A ratio compares two quantities, while a proportion states that two ratios are equal. A proportion is an equation involving two ratios.
Q: Are there any online tools that can help me calculate ratios and percentages?
A: Yes, many online calculators are available that can perform these calculations quickly and easily. However, understanding the underlying principles remains crucial.
Q: How can I improve my understanding of ratios and percentages?
A: Practice is key. Try solving various problems involving ratios and percentages. Consult educational resources, such as textbooks and online tutorials, for a comprehensive understanding.
Conclusion
Understanding "25 out of 105," its various representations, and its application within the broader concepts of ratios, percentages, and proportions is a fundamental skill applicable across various domains. Mastering these concepts empowers us to interpret data effectively, solve problems efficiently, and make informed decisions in both academic and real-world contexts. By grasping the underlying principles and practicing regularly, individuals can confidently navigate the world of mathematical proportions and percentages, unlocking a deeper understanding of quantitative analysis and its significance in our lives. Remember that the ability to convert between fractions, decimals, and percentages is an invaluable tool that transcends the simple example of 25 out of 105 and applies to a vast array of situations. So, keep practicing, keep learning, and keep exploring the fascinating world of mathematics!
Latest Posts
Latest Posts
-
Port Udp 137
Sep 23, 2025
-
4cm Into Mm
Sep 23, 2025
-
Tidal Volume Calculator
Sep 23, 2025
-
Ounces In 375ml
Sep 23, 2025
-
Formula Sodium Sulfide
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 105 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.