25 1 2
interactiveleap
Sep 24, 2025 · 6 min read
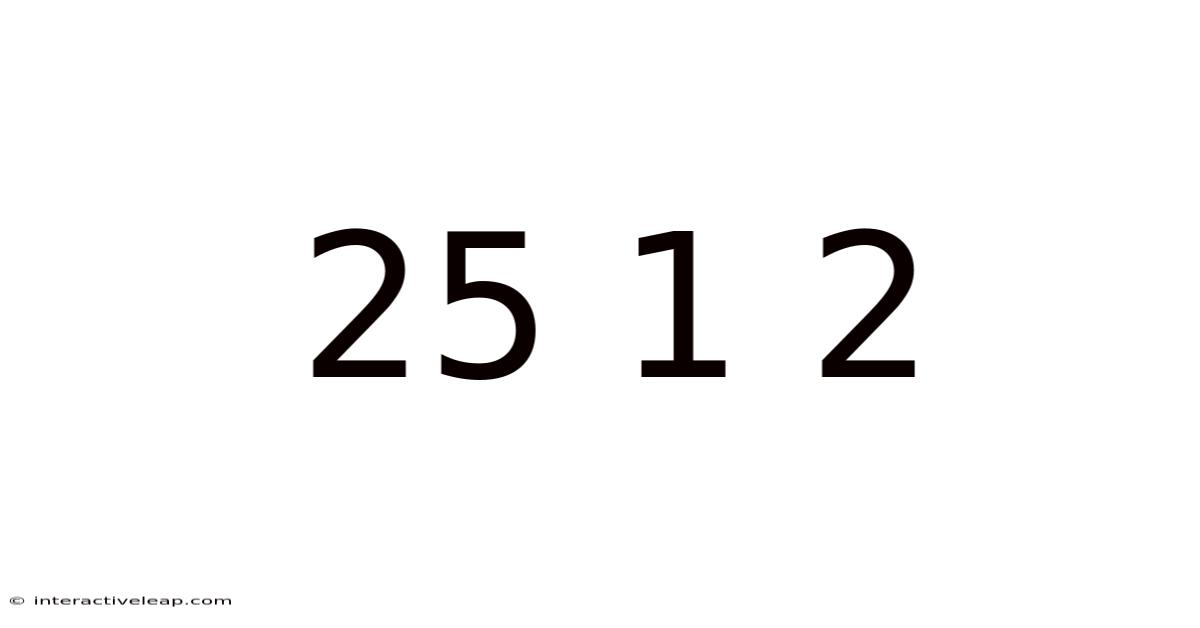
Table of Contents
Decoding 2512: A Deep Dive into Number Theory, Combinatorics, and Problem Solving
The seemingly simple sequence "2512" holds a surprising depth of mathematical possibilities. At first glance, it's just a four-digit number. However, a closer examination reveals connections to number theory, combinatorics, and various problem-solving approaches. This article will explore the multifaceted nature of 2512, examining its prime factorization, its role in combinatorics, and how it can be used to illustrate fundamental mathematical concepts. We'll delve into practical examples, explore related theorems, and unravel the intriguing layers hidden within this seemingly ordinary number.
I. Number Theory: Prime Factorization and Divisibility
The most fundamental aspect of understanding any integer is its prime factorization. Prime factorization is the process of expressing a number as the product of its prime factors – numbers divisible only by 1 and themselves. Let's find the prime factorization of 2512:
- Step 1: We can start by dividing 2512 by the smallest prime number, 2. 2512 ÷ 2 = 1256.
- Step 2: 1256 is also divisible by 2: 1256 ÷ 2 = 628.
- Step 3: Again, 628 is divisible by 2: 628 ÷ 2 = 314.
- Step 4: 314 is divisible by 2: 314 ÷ 2 = 157.
- Step 5: 157 is a prime number.
Therefore, the prime factorization of 2512 is 2<sup>4</sup> x 157. This factorization immediately tells us several things:
- Divisors: The number of divisors of 2512 can be calculated using the formula (a+1)(b+1)... where a, b... are the exponents in the prime factorization. In this case, it's (4+1)(1+1) = 10. Therefore, 2512 has 10 divisors.
- Divisibility Rules: We know 2512 is divisible by 2, 4, 8, and 157 (and combinations thereof). This knowledge is crucial in various mathematical problems involving divisibility tests.
II. Combinatorics: Permutations and Combinations
The digits of 2512 – 2, 5, 1, and 2 – can be used to illustrate concepts in combinatorics, specifically permutations and combinations.
-
Permutations: A permutation is an arrangement of objects in a specific order. If we consider the four digits of 2512 as distinct objects, even though there are two 2s, we can find the number of permutations. However, since we have repeated digits, we need to account for this repetition. The formula for permutations with repetitions is: n! / (n1! n2! ...), where n is the total number of objects and n1, n2... are the counts of each repeated object. In our case, n = 4, n1 = 2 (for the two 2s). Therefore, the number of permutations is 4! / 2! = 12.
-
Combinations: A combination is a selection of objects where the order doesn't matter. If we wanted to select, say, two digits from 2512, the number of combinations would be calculated using the combination formula: nCr = n! / (r!(n-r)!), where n is the total number of objects and r is the number of objects to be selected. For example, choosing two digits from 2512 (considering the repeated 2 as distinct for this example): 4C2 = 4! / (2!(4-2)!) = 6. However, if we consider the two 2s as identical, we would need a different approach, treating this as a combination with repetition, requiring more complex combinatorial techniques.
III. Problem Solving: Applications of 2512
The number 2512 can be used as a basis for various mathematical problems. Here are a few examples:
-
Diophantine Equations: We can construct Diophantine equations (equations with integer solutions) using 2512. For example, finding integer solutions for x + y = 2512 or ax + by = 2512, where a and b are integers. The solvability of such equations depends on the properties of 2512 (its prime factorization and divisors).
-
Modular Arithmetic: 2512 can be used in modular arithmetic problems. For example, finding the remainder when 2512 is divided by a given integer (e.g., 2512 mod 7). The remainder will depend on the properties of both 2512 and the divisor.
-
Number Puzzles: 2512 can serve as the target number in various number puzzles involving arithmetic operations (+, -, *, /). Such puzzles challenge the solver to find a sequence of operations using a given set of numbers to arrive at 2512.
-
Sequences and Series: We could create mathematical sequences and series that involve 2512. For instance, an arithmetic progression where 2512 is a term or a geometric progression where 2512 is related to the terms.
IV. Geometric Representation
While not directly obvious, the number 2512 can be visualized geometrically. For example:
-
Area: We can imagine a rectangle with an area of 2512 square units. The dimensions of the rectangle would be pairs of factors of 2512. Given its prime factorization (2⁴ x 157), the possible dimensions are numerous.
-
Volume: Extending this to three dimensions, we can consider a rectangular prism with a volume of 2512 cubic units. Finding the possible dimensions involves finding sets of three factors whose product is 2512.
V. Advanced Concepts and Extensions
The exploration of 2512 can extend to more advanced mathematical concepts:
-
Cryptography: Prime factorization plays a crucial role in cryptography. While the factorization of 2512 is relatively straightforward, the difficulty of factoring very large numbers into their prime factors is the basis of many modern encryption algorithms.
-
Abstract Algebra: Concepts from abstract algebra, like groups and rings, can be applied to analyze the properties of numbers like 2512 within specific algebraic structures.
-
Number Theory Theorems: Theorems from number theory, such as Fermat's Little Theorem or the Chinese Remainder Theorem, could be used to solve problems involving 2512.
VI. Frequently Asked Questions (FAQ)
-
Q: What is the sum of the digits of 2512?
- A: The sum of the digits is 2 + 5 + 1 + 2 = 10.
-
Q: Is 2512 a perfect square?
- A: No, 2512 is not a perfect square because its prime factorization contains an odd exponent for the prime factor 157.
-
Q: Is 2512 divisible by 3?
- A: No, 2512 is not divisible by 3 because the sum of its digits (10) is not divisible by 3.
-
Q: How many factors does 2512 have?
- A: 2512 has 10 factors.
VII. Conclusion
The number 2512, initially appearing simple, provides a rich landscape for exploring fundamental mathematical concepts. From its prime factorization and divisibility rules to its applications in combinatorics, problem-solving, and geometric representations, 2512 serves as a microcosm of number theory's breadth and depth. By exploring this seemingly ordinary number, we gain a deeper appreciation for the intricate connections and patterns that underlie the world of mathematics. The exploration can extend to much more complex areas, demonstrating how even seemingly simple numbers can lead to surprisingly profound mathematical insights. The analysis of 2512 is not merely an exercise in calculation, but a journey into the core principles that govern the behavior of integers and their relationships. This deeper understanding fosters a more intuitive and insightful approach to problem-solving and encourages further exploration of the vast and fascinating field of mathematics.
Latest Posts
Latest Posts
-
66 3kg In Lbs
Sep 24, 2025
-
Costume Headless Horseman
Sep 24, 2025
-
Cross Dock Warehouse
Sep 24, 2025
-
20 Of 335
Sep 24, 2025
-
Native American Pattern
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 25 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.