240 / 3
interactiveleap
Sep 15, 2025 · 5 min read
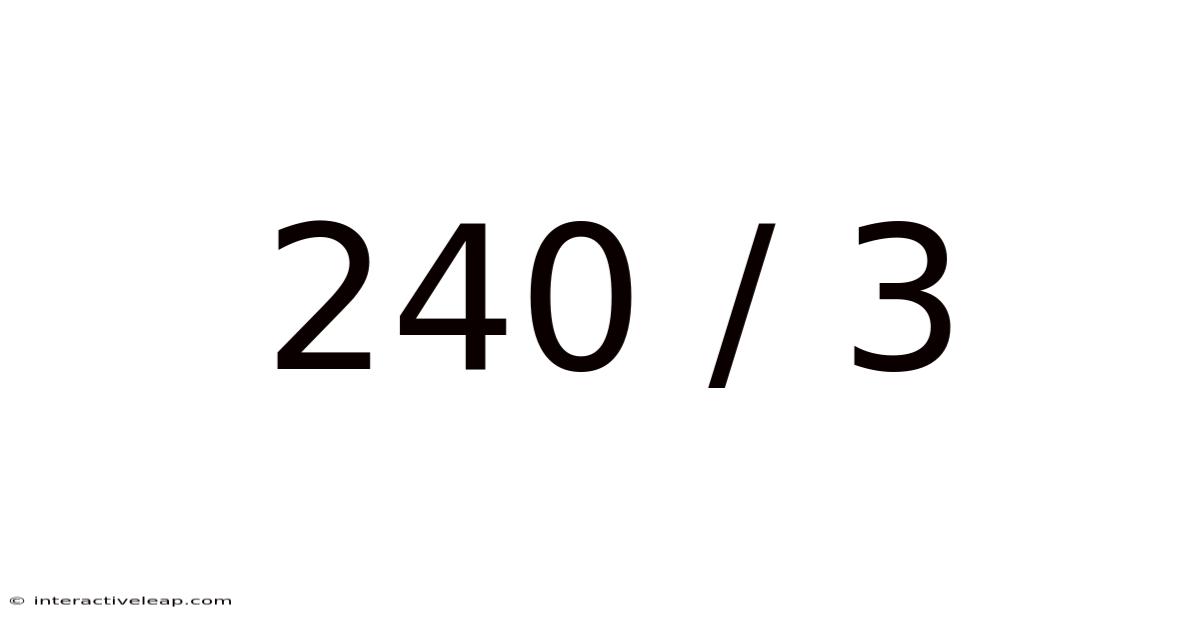
Table of Contents
Decoding 240 / 3: A Deep Dive into Division and its Applications
This article explores the seemingly simple division problem, 240 / 3, going beyond the answer to delve into the underlying mathematical concepts, practical applications, and related problem-solving strategies. We’ll cover various methods for solving this problem, examine its relevance in different fields, and address frequently asked questions. Understanding division isn't just about getting the right answer; it's about grasping the fundamental principles that govern many aspects of our quantitative world.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially represents the process of splitting a quantity into equal parts. In the expression 240 / 3, we're asking: "How many times does 3 go into 240?" or equivalently, "What is the result of splitting 240 into 3 equal groups?"
The terms used in division are important:
- Dividend: The number being divided (240 in this case).
- Divisor: The number we are dividing by (3 in this case).
- Quotient: The result of the division (the answer).
- Remainder: The amount left over if the division doesn't result in a whole number. In this specific example, there will be no remainder.
Methods for Solving 240 / 3
Several methods can be used to solve 240 / 3. Let's explore a few:
1. Long Division
Long division is a standard algorithm taught in schools. It involves a systematic process of repeatedly subtracting the divisor from the dividend until the remainder is less than the divisor.
80
3 | 240
-24
00
-0
0
This shows that 3 goes into 240 eighty times.
2. Repeated Subtraction
This method involves repeatedly subtracting the divisor (3) from the dividend (240) until you reach zero. The number of times you subtract represents the quotient. While effective for smaller numbers, it becomes less practical for larger dividends.
240 - 3 = 237 237 - 3 = 234 ...and so on until you reach 0. Counting the number of subtractions will give you the answer, 80.
3. Mental Math & Factoring
For those familiar with multiplication tables, solving 240 / 3 can be done mentally. Knowing that 3 x 80 = 240 immediately provides the answer. This method relies on recognizing factors and their relationships.
4. Using a Calculator
Calculators provide a quick and efficient way to solve division problems. Simply input 240 / 3 and the calculator will instantly display the answer: 80. While convenient, it's crucial to understand the underlying mathematical principles even when using a calculator.
Real-World Applications of Division: Beyond the Classroom
Division isn't just a mathematical concept; it's a tool used extensively in various fields:
-
Finance: Calculating equal monthly payments on a loan, splitting costs among multiple people, determining profit margins, and analyzing financial statements all involve division.
-
Engineering: In construction, calculating the amount of materials needed, dividing space into sections, and determining load distribution require precise division. In software engineering, it's used in algorithms and resource allocation.
-
Science: Many scientific calculations, experiments, and data analysis rely heavily on division. Averaging data sets, calculating concentrations, and determining ratios all require division.
-
Cooking & Baking: Scaling recipes up or down, dividing ingredients equally, and calculating serving sizes all necessitate division.
-
Everyday Life: Sharing items equally among friends, splitting bills, calculating fuel efficiency, and determining unit prices all involve division.
Exploring Related Concepts: Fractions and Decimals
The problem 240 / 3 is easily solved, resulting in a whole number. However, understanding division extends to scenarios involving fractions and decimals.
Consider a related problem: 241 / 3. This division results in a quotient of 80 with a remainder of 1. This remainder can be expressed as a fraction (1/3) or a decimal (0.333...). This introduces the concepts of improper fractions, mixed numbers, and decimal representation, expanding our understanding of division beyond whole numbers.
Understanding how to handle remainders and convert them into fractions or decimals is crucial for solving more complex problems and applying division to real-world scenarios where precise answers might not always be whole numbers.
Expanding the Concept: Division with Larger Numbers and Decimals
While 240 / 3 provides a straightforward example, the principles of division apply to much larger numbers and decimals. For instance, consider a problem such as 3785 / 12. This would require the application of long division or the use of a calculator to obtain the solution. However, the underlying principles remain the same: understanding the dividend, divisor, quotient, and potentially, the remainder.
When dealing with decimals, the process remains similar but requires careful attention to decimal placement. For example, 24.0 / 3 would still yield a quotient of 8.0, showcasing the consistency of the process across different numerical forms.
Frequently Asked Questions (FAQs)
Q: What if the divisor is zero?
A: Dividing by zero is undefined in mathematics. It's a fundamental rule that you cannot divide any number by zero. Attempting to do so will result in an error on a calculator or an undefined result in mathematical calculations.
Q: How can I improve my division skills?
A: Practice is key! Start with simpler problems and gradually work your way up to more complex ones. Regular practice with long division and mental math will enhance your speed and accuracy. Understanding multiplication tables thoroughly will also significantly improve your division skills.
Q: Are there different types of division?
A: While the basic concept remains consistent, division can be approached in different ways, such as the methods outlined earlier (long division, repeated subtraction, mental math). The choice of method often depends on the complexity of the problem and the available tools.
Q: What are some common mistakes to avoid in division?
A: Common mistakes include errors in long division (incorrect placement of numbers, miscalculations), forgetting to account for remainders, and incorrectly handling decimals. Careful attention to detail and methodical calculation can minimize these errors.
Conclusion: Mastering Division for a More Numerate Life
The seemingly simple problem 240 / 3 provides a gateway to understanding a fundamental mathematical operation with far-reaching applications. This article has explored various methods for solving this problem and extended the discussion to encompass related concepts such as fractions, decimals, and the importance of handling remainders. By mastering division, we enhance our ability to tackle more complex mathematical problems and confidently apply these skills to various aspects of our lives – from financial planning and scientific endeavors to everyday tasks and problem-solving. Remember, the key to success is consistent practice and a solid understanding of the underlying principles. So, keep practicing, keep exploring, and keep expanding your mathematical horizons!
Latest Posts
Latest Posts
-
210 Divided 3
Sep 15, 2025
-
15 Of 140
Sep 15, 2025
-
75 90 Simplified
Sep 15, 2025
-
Education Of Sparta
Sep 15, 2025
-
1 68m In Ft
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 240 / 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.