21 X 12
interactiveleap
Sep 14, 2025 · 6 min read
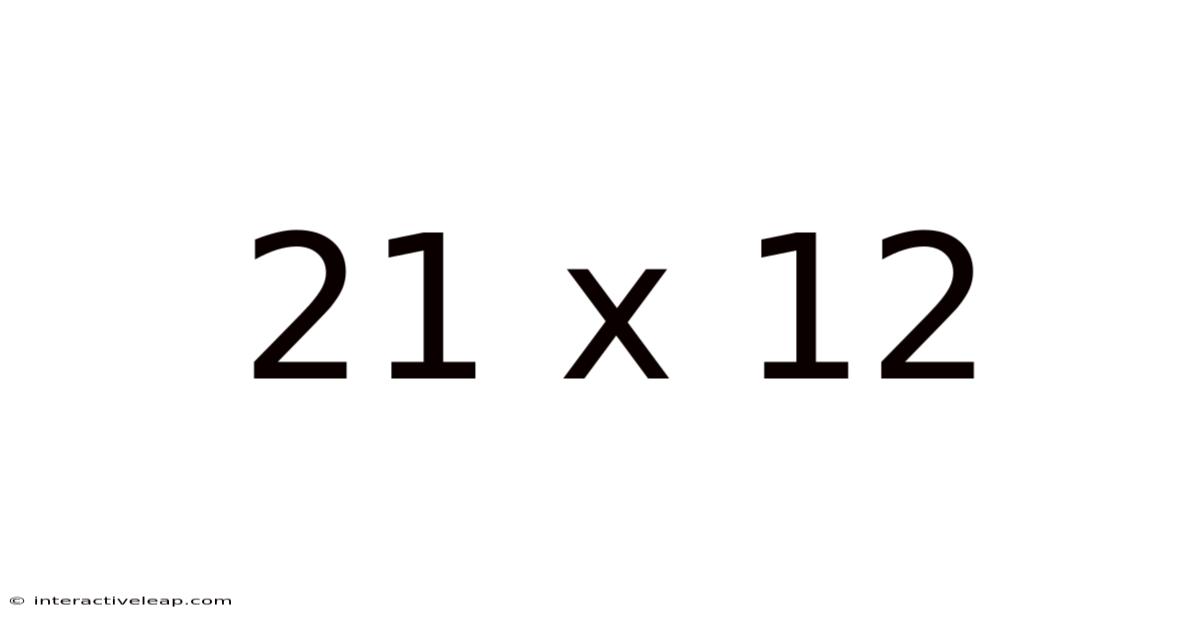
Table of Contents
Unveiling the Secrets of 21 x 12: More Than Just a Multiplication Problem
The seemingly simple multiplication problem, 21 x 12, holds far more educational value than meets the eye. This article delves into the various methods for solving this problem, explores its applications in different fields, and expands on the underlying mathematical concepts, making it a valuable resource for students, teachers, and anyone interested in deepening their mathematical understanding. We'll move beyond a simple answer and uncover the rich tapestry of knowledge woven into this seemingly basic calculation.
Introduction: More Than Just an Answer
At first glance, 21 x 12 appears as a straightforward multiplication problem. A quick calculation reveals the answer: 252. However, the beauty of mathematics lies not just in finding the answer but in understanding the process and the underlying principles. This article will explore various methods to solve 21 x 12, highlighting the versatility and elegance of mathematical techniques. We'll explore the distributive property, the lattice method, and even consider mental math strategies. Beyond the calculation itself, we will investigate the practical applications of this calculation in diverse fields, from everyday budgeting to advanced engineering calculations.
Method 1: The Standard Algorithm
The most common approach is the standard multiplication algorithm taught in schools. This method involves multiplying each digit of one number by each digit of the other number and then adding the partial products.
- Step 1: Multiply 21 by 2 (the tens digit of 12). 21 x 2 = 42. Write 42 below.
- Step 2: Multiply 21 by 1 (the units digit of 12). 21 x 1 = 21. Write 21 below, shifted one place to the left.
- Step 3: Add the partial products: 42 + 210 = 252.
Therefore, 21 x 12 = 252. This method is systematic and reliable, forming a solid foundation for more complex multiplication problems.
Method 2: The Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this property to break down the problem into simpler calculations:
- Rewrite 12 as 10 + 2.
- Apply the distributive property: 21 x (10 + 2) = (21 x 10) + (21 x 2)
- Calculate: (210) + (42) = 252
This method demonstrates a fundamental algebraic principle, showcasing the interconnectedness of different mathematical concepts. It’s especially helpful in mental math, breaking down a larger problem into smaller, manageable parts.
Method 3: The Lattice Method
The lattice method, a visually appealing and efficient technique, is particularly useful for larger multiplication problems. While it might seem initially complex, it offers a systematic approach with minimal carrying, reducing errors.
- Step 1: Draw a grid (a 2x2 square) with diagonals within each smaller square.
- Step 2: Write 21 along the top and 12 down the right side.
- Step 3: Multiply each digit individually. For example, 2 x 1 = 2 (top left square), 2 x 2 = 4 (bottom left), 1 x 1 = 1 (top right), 1 x 2 = 2 (bottom right). Write the tens digit above the diagonal and the units digit below.
- Step 4: Add the diagonal numbers, starting from the bottom right. 2 + 1 + 4 = 7 (units place). Then, 2 + 0 + 2 = 4 (tens place). And finally, 0 + 0 = 0 (hundreds place).
- Step 5: Concatenate the sums to obtain the final answer: 252.
Method 4: Mental Math Techniques
Mastering mental math is a valuable skill. For 21 x 12, we can leverage our understanding of place value and distributive property:
- Think of 21 as 20 + 1.
- Multiply 20 x 12 = 240.
- Multiply 1 x 12 = 12.
- Add the results: 240 + 12 = 252.
This approach requires practice and a good understanding of number relationships, but it's a powerful tool for quick calculations. You can further break this down: 12 x 20 is the same as 12 x 2 x 10 which many can easily calculate as 24 x 10 = 240.
Applications of 21 x 12 in Real-World Scenarios
While 21 x 12 might seem like an abstract mathematical exercise, its applications extend far beyond the classroom.
- Business and Finance: Calculating the total cost of 21 items priced at $12 each.
- Construction and Engineering: Determining the area of a rectangular space measuring 21 feet by 12 feet.
- Everyday Life: Figuring out the total number of cookies in 21 boxes, each containing 12 cookies.
- Data Analysis: Calculating the total number of data points in a 21 x 12 data matrix.
- Computer Programming: Looping or iterative processes might involve calculations similar to this.
Mathematical Concepts Illustrated
The seemingly simple calculation of 21 x 12 provides a practical illustration of several key mathematical concepts:
- Multiplication: The fundamental operation of repeated addition.
- Distributive Property: A key principle in algebra and number theory.
- Place Value: Understanding the value of digits based on their position.
- Factors and Multiples: 21 and 12 have various factors, and their product, 252, is a multiple of both.
- Prime Factorization: Breaking down numbers into their prime factors. 252 = 2 x 2 x 3 x 3 x 7
Expanding the Scope: Exploring Related Calculations
Understanding 21 x 12 allows us to approach related problems with ease. For example:
- Calculating 21 x 24 (double the value of 12).
- Calculating 42 x 12 (double the value of 21).
- Calculating 21 x 11 (one less than 12).
These related problems help reinforce the understanding of multiplicative relationships and the impact of changing one or both operands.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest method to solve 21 x 12? A: The easiest method depends on your personal preference and mathematical strengths. The distributive property or mental math techniques might be quicker for some, while others might prefer the standard algorithm.
-
Q: What are some real-world applications of this calculation beyond the examples given? A: Applications are virtually limitless. Any scenario involving the combination of 21 units of something with 12 units of another (or vice-versa) requires this calculation. Consider quantities of items, lengths, areas, or any scenario where you need to multiply these two numbers.
-
Q: How can I improve my multiplication skills? A: Practice is key! Regularly work on multiplication problems of varying difficulty. Utilize different methods to find the best approach for you. Use flashcards, online games, or workbooks designed to improve multiplication skills.
-
Q: Is there a shortcut for multiplying numbers ending in 0? A: Yes, multiplying by multiples of 10 simply involves adding zeros to the end of the other number. For instance, 21 x 10 = 210.
Conclusion: Beyond the Numbers
The seemingly mundane calculation of 21 x 12 opens a window into the fascinating world of mathematics. It's more than just an answer; it's a pathway to understanding fundamental mathematical principles, diverse problem-solving techniques, and their applications in a wide range of fields. By exploring different methods and considering real-world examples, we've broadened our understanding of this seemingly simple problem, revealing its hidden depth and practical relevance. The journey from a simple multiplication problem to a comprehensive understanding of underlying mathematical concepts highlights the beauty and power of mathematical thinking. Continue exploring, experimenting with different methods, and you'll find mathematics becomes less of a chore and more of an engaging and rewarding intellectual pursuit.
Latest Posts
Latest Posts
-
70 Of 65
Sep 14, 2025
-
Lee Friedlander Photographer
Sep 14, 2025
-
300pounds In Kg
Sep 14, 2025
-
147 Pounds Kg
Sep 14, 2025
-
4 Of 50
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 21 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.