21 Of 320
interactiveleap
Sep 21, 2025 · 5 min read
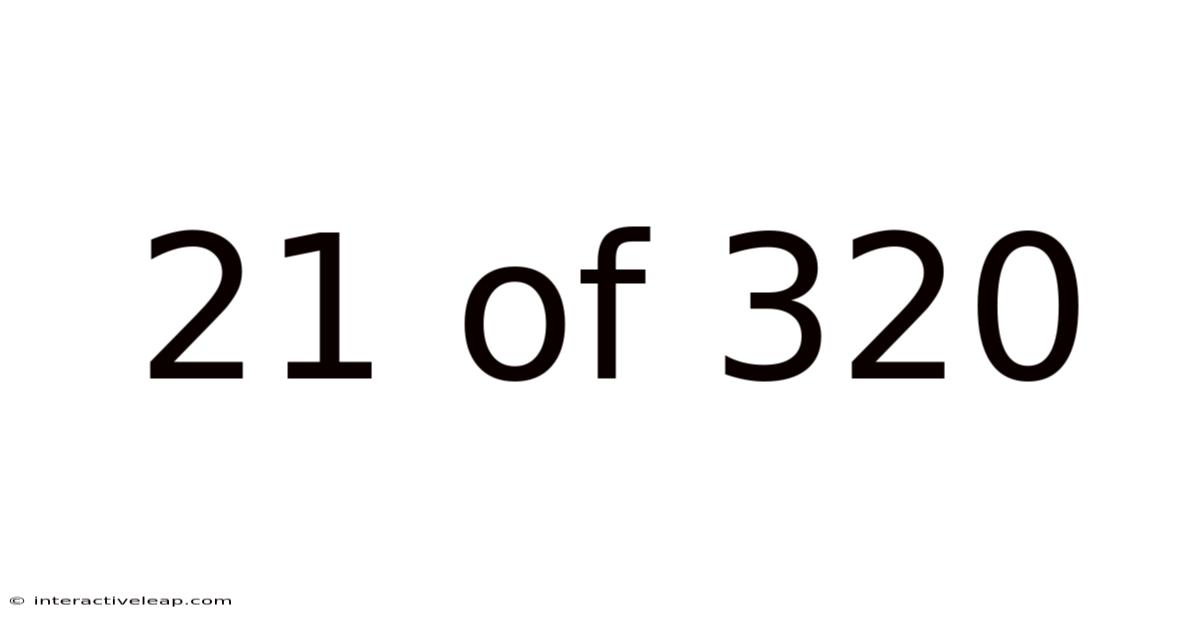
Table of Contents
Decoding the Enigma: Unveiling the Significance of 21 out of 320
The seemingly simple fraction, 21 out of 320, holds a surprising depth of meaning depending on its context. This article will explore the various interpretations and applications of this ratio, moving beyond simple arithmetic to delve into its potential significance in fields ranging from statistics and probability to data analysis and even symbolic interpretation. Understanding the significance of 21 out of 320 requires us to consider the broader context in which this ratio appears. Whether it represents a success rate, a sample proportion, or something else entirely, fundamentally changes its meaning and implications.
Understanding the Basic Calculation: 21/320
At its core, 21 out of 320 is a simple ratio representing a part-to-whole relationship. It can be expressed as a fraction (21/320), a decimal (approximately 0.065625), or a percentage (approximately 6.56%). This basic calculation provides a foundational understanding, serving as a springboard for further analysis depending on the context. A simple calculation reveals that approximately 6.56% of the total (320) is represented by the value 21.
Contextualizing the Ratio: Where Does 21/320 Appear?
The true significance of 21 out of 320 hinges entirely on its context. Consider these scenarios:
-
Medical Trials: In a clinical trial with 320 participants, 21 experiencing a positive outcome (e.g., remission from a disease) might suggest a low but potentially significant treatment efficacy. Further statistical analysis, including confidence intervals and p-values, would be necessary to determine the clinical significance of this result. The ratio might be considered statistically significant depending on pre-determined alpha levels.
-
Market Research: If 21 out of 320 surveyed consumers expressed preference for a particular product, this would represent a relatively low market share. This information could inform marketing strategies, perhaps highlighting the need for targeted advertising campaigns to increase brand awareness and consumer preference.
-
Quality Control: In a manufacturing process where 320 items are inspected, finding 21 defective items represents a 6.56% defect rate. This rate might be considered acceptable or unacceptable depending on industry standards and the potential consequences of defective products. The significance lies in determining whether corrective actions are required to reduce the defect rate.
-
Educational Assessment: If 21 out of 320 students passed a particular exam, this indicates a low pass rate, signifying potential issues within the curriculum, teaching methodology, or student preparedness. Further investigation would be necessary to identify and address the underlying causes of this poor performance.
-
Environmental Studies: In an ecological study, if 21 out of 320 sampled plants exhibited a specific disease, this could indicate the prevalence of that disease within the studied population. Further research could then focus on identifying the cause of the disease and strategies for mitigation.
Statistical Significance and Interpretation
When dealing with proportions like 21/320, statistical tools become crucial for proper interpretation. These tools help to determine whether the observed proportion is merely due to chance or represents a genuine effect. Key statistical concepts include:
-
Confidence Intervals: These provide a range of values within which the true population proportion is likely to fall with a certain degree of confidence (e.g., a 95% confidence interval). A narrow confidence interval indicates a more precise estimate.
-
Hypothesis Testing: This involves formulating a null hypothesis (e.g., there is no difference in outcome between groups) and testing it against an alternative hypothesis using statistical tests (e.g., z-test, chi-square test). The p-value, obtained from these tests, indicates the probability of observing the data if the null hypothesis is true. A low p-value (typically below 0.05) suggests that the null hypothesis should be rejected, implying statistical significance.
-
Sample Size: The sample size (320 in this case) influences the precision of the estimate. Larger sample sizes generally lead to narrower confidence intervals and more reliable conclusions. With a sample size of 320, the results are generally considered reasonably reliable, provided the sampling method was appropriate. However, depending on the variability of the data, a larger sample size might be needed for greater accuracy.
Beyond the Numbers: Symbolic Interpretations
While primarily a numerical ratio, 21 out of 320 might also hold symbolic meaning depending on the context. The numbers themselves could be considered significant in various cultural or religious traditions. For instance, the number 21 might be associated with maturity or coming of age, while 320 could have no specific symbolic connotation. However, without a clearly defined cultural or symbolic framework, these interpretations remain speculative. Focusing on the numerical context and statistical analysis remains the most reliable approach.
Frequently Asked Questions (FAQs)
Q: How do I calculate the percentage represented by 21 out of 320?
A: To calculate the percentage, divide 21 by 320 and then multiply by 100: (21/320) * 100 ≈ 6.56%.
Q: Is 21 out of 320 statistically significant?
A: The statistical significance of 21 out of 320 depends entirely on the context and the type of statistical test used. Without knowing the specific research question and the nature of the data, it's impossible to determine statistical significance. Additional data and statistical analysis are necessary.
Q: What are the limitations of interpreting 21 out of 320 without additional information?
A: The main limitation is the lack of context. Knowing the nature of the data (e.g., success rate in a medical trial, consumer preference in a market survey) is crucial for accurate interpretation. Moreover, understanding the sampling method used to obtain the data is essential to avoid bias.
Q: How can I improve the precision of my estimate?
A: Increasing the sample size would improve the precision of the estimate. A larger sample size leads to narrower confidence intervals and more reliable conclusions. Careful consideration of the sampling method to avoid bias is also crucial.
Conclusion: The Power of Context in Data Interpretation
The seemingly simple ratio of 21 out of 320 reveals its true significance only within its context. While a simple calculation provides a basic understanding, applying statistical tools and carefully considering the nature of the data are crucial for a meaningful interpretation. From medical trials and market research to quality control and environmental studies, the ratio's implications vary greatly depending on the field of application. Remember, numbers alone tell only part of the story. It's the context, the analytical framework, and the understanding of underlying factors that unlock the full meaning of data like 21 out of 320. Approaching data analysis with a critical and nuanced perspective is key to extracting actionable insights.
Latest Posts
Latest Posts
-
3 Times 12
Sep 21, 2025
-
3 Of 210
Sep 21, 2025
-
Decimal Of 1 7
Sep 21, 2025
-
40 Of 3500
Sep 21, 2025
-
10 Of 14
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 21 Of 320 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.