20 Of 400
interactiveleap
Sep 24, 2025 · 5 min read
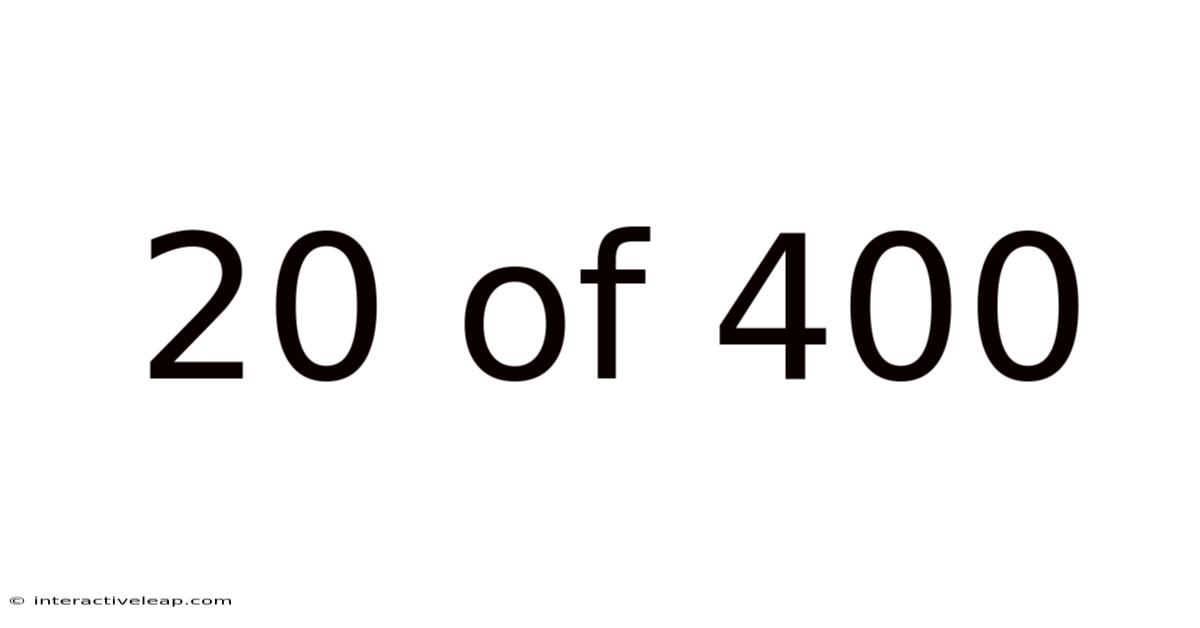
Table of Contents
Decoding the Mystery: Understanding the Fraction 20/400 and its Implications
The seemingly simple fraction 20/400 might appear insignificant at first glance. However, understanding this fraction unlocks a deeper appreciation of mathematical concepts like simplification, ratios, proportions, and percentages – fundamental skills applicable across various fields, from finance and engineering to everyday decision-making. This article will delve into the intricacies of 20/400, exploring its simplification, practical applications, and broader mathematical implications. We’ll also address frequently asked questions and highlight its relevance in different contexts.
Simplifying the Fraction: From 20/400 to its Simplest Form
The first step in understanding any fraction is to simplify it to its lowest terms. This process involves finding the greatest common divisor (GCD) of the numerator (20) and the denominator (400). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
In this case, the GCD of 20 and 400 is 20. We divide both the numerator and the denominator by 20:
20 ÷ 20 = 1 400 ÷ 20 = 20
Therefore, the simplified form of 20/400 is 1/20. This simplified fraction represents the same value as 20/400 but is more concise and easier to work with in calculations.
Understanding Ratios and Proportions: The Meaning of 1/20
The simplified fraction 1/20 can be interpreted as a ratio. A ratio is a comparison of two quantities. In this case, it compares one part to twenty parts. This ratio can be expressed in several ways:
- 1:20: This is the most common way to represent a ratio.
- One to twenty: This is a verbal representation of the ratio.
- 1 out of 20: This describes the probability or occurrence of one event out of a total of twenty possible events.
Understanding proportions is crucial when dealing with ratios. A proportion is a statement that two ratios are equal. For instance, if we have a proportion involving 1/20, we can set it up as follows:
1/20 = x/100
To solve for x (the unknown quantity), we cross-multiply:
1 * 100 = 20 * x 100 = 20x x = 5
This shows that 5 out of 100 is equivalent to 1 out of 20. This principle of proportionality is essential in various applications, such as scaling recipes, calculating percentages, and solving problems in geometry and physics.
Converting to Percentage: Expressing 1/20 as a Percentage
Percentages are a common way to represent fractions and ratios. To convert the fraction 1/20 to a percentage, we divide the numerator (1) by the denominator (20) and then multiply the result by 100%:
(1 ÷ 20) * 100% = 0.05 * 100% = 5%
Therefore, 20/400, or its simplified form 1/20, is equivalent to 5%. This representation is particularly useful for comparing proportions and making data easier to understand.
Practical Applications of 20/400 (or 1/20 and 5%): Real-World Examples
The fraction 20/400, and its simplified equivalents, has numerous practical applications in various fields:
-
Finance: Imagine investing $400 and earning a profit of $20. Your return on investment (ROI) would be 20/400, or 5%. This is a standard calculation used to assess the profitability of investments.
-
Statistics and Probability: If 20 out of 400 people surveyed prefer a particular brand, then the proportion of people who prefer that brand is 5%. This data is crucial for market research and product development.
-
Engineering and Measurement: In engineering, ratios and proportions are used extensively in scaling blueprints, calculating material quantities, and ensuring accuracy in designs. A ratio of 1:20 could represent the scale of a model relative to the actual structure.
-
Everyday Life: If you have 400 candies and you give away 20, you have given away 5% of your candies.
-
Education: If a student answers 20 out of 400 questions correctly on a test, their score is 5%. This helps to evaluate performance and identify areas needing improvement.
Further Mathematical Implications: Exploring Decimal Representation and More
The fraction 20/400, or 1/20, can also be expressed as a decimal:
1 ÷ 20 = 0.05
This decimal representation is useful for calculations involving other decimal numbers. Furthermore, understanding this fraction helps solidify understanding of:
-
Equivalent Fractions: Many fractions can be simplified to 1/20, such as 5/100, 10/200, and so on. Understanding this reinforces the concept that fractions representing the same ratio are equivalent.
-
Fraction Operations: Applying arithmetic operations (addition, subtraction, multiplication, division) to fractions like 1/20 strengthens fundamental algebraic skills.
-
Number Systems: Representing 1/20 in different forms (fraction, decimal, percentage) deepens understanding of the relationship between different number systems.
Frequently Asked Questions (FAQs)
Q1: What is the simplest form of 20/400?
A1: The simplest form of 20/400 is 1/20.
Q2: How do I convert 20/400 to a percentage?
A2: Divide the numerator (20) by the denominator (400) and multiply by 100%. This yields 5%.
Q3: What is the decimal equivalent of 20/400?
A3: The decimal equivalent of 20/400 is 0.05.
Q4: What are some real-world applications of this fraction?
A4: This fraction can be applied in finance (ROI), statistics (percentages), engineering (scaling), and everyday situations (proportions).
Q5: Can 1/20 be further simplified?
A5: No, 1/20 is already in its simplest form because the greatest common divisor of 1 and 20 is 1.
Conclusion: The Significance of Understanding Fractions
The seemingly insignificant fraction 20/400 holds a significant place in understanding fundamental mathematical principles. By simplifying it to 1/20 and exploring its various representations (ratio, percentage, decimal), we gain a deeper appreciation of ratios, proportions, and percentages—concepts with wide-ranging applications in various fields. This exploration not only clarifies the specific mathematical aspects of 20/400 but also builds a stronger foundation in numerical literacy, empowering you to tackle more complex mathematical problems and real-world scenarios with greater confidence. Remember, mastering fundamental concepts like fractions is key to unlocking a deeper understanding of mathematics and its practical applications in everyday life.
Latest Posts
Latest Posts
-
25 Of 47
Sep 24, 2025
-
Symbols Of Courage
Sep 24, 2025
-
45kph To Mph
Sep 24, 2025
-
15 Of 42 00
Sep 24, 2025
-
90 Into Feet
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.