2 X 3/12
interactiveleap
Sep 15, 2025 · 5 min read
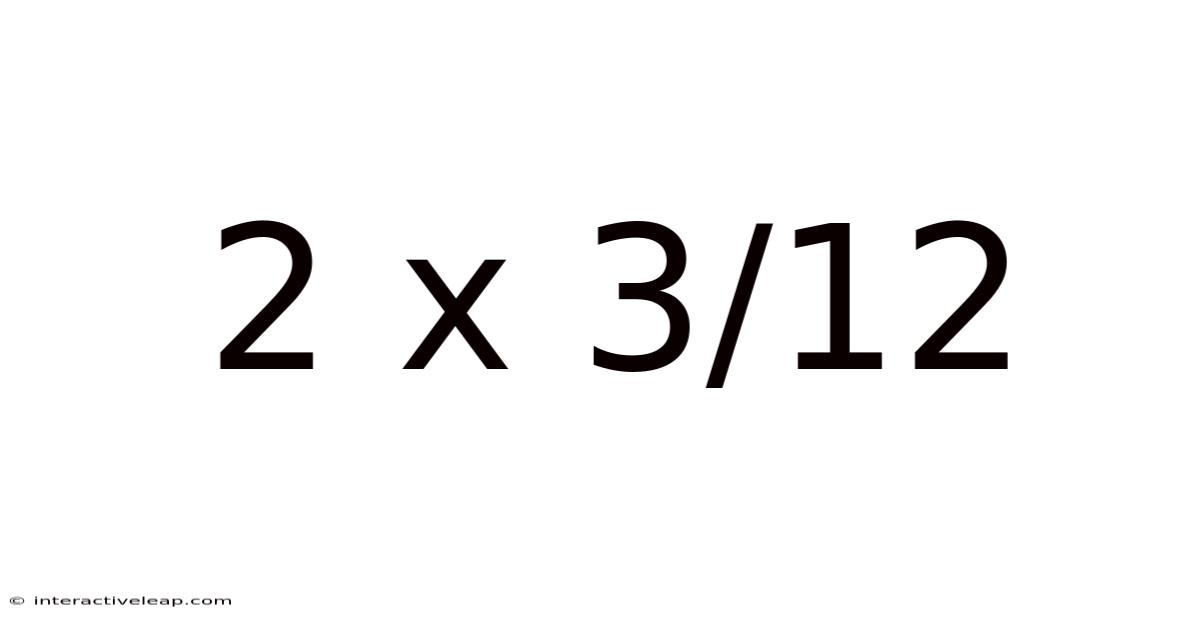
Table of Contents
Decoding 2 x 3/12: A Deep Dive into Fraction Multiplication and its Applications
This article explores the seemingly simple mathematical expression "2 x 3/12," delving beyond the immediate answer to uncover the fundamental principles of fraction multiplication and its broader applications in various fields. We will unpack the process step-by-step, examine the underlying mathematical concepts, and explore real-world examples to solidify your understanding. This comprehensive guide is suitable for learners of all levels, from those revisiting basic arithmetic to those seeking a deeper grasp of fractional calculations. Understanding fraction multiplication is crucial for success in algebra, calculus, and countless practical applications.
Understanding the Basics: Fractions and Multiplication
Before tackling "2 x 3/12," let's refresh our understanding of fractions and multiplication. A fraction represents a part of a whole. It's composed of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, 3/4 represents 3 parts out of a total of 4 equal parts.
Multiplication, in its simplest form, is repeated addition. When we multiply 2 x 3, we're essentially adding 3 two times (3 + 3 = 6). However, when multiplying with fractions, the concept extends to finding a portion of a portion.
Step-by-Step Calculation of 2 x 3/12
Now, let's solve "2 x 3/12":
-
Rewrite the Whole Number as a Fraction: Any whole number can be expressed as a fraction with a denominator of 1. Therefore, we rewrite 2 as 2/1. Our expression now becomes (2/1) x (3/12).
-
Multiply the Numerators: Multiply the numerators together: 2 x 3 = 6. This becomes the numerator of our answer.
-
Multiply the Denominators: Multiply the denominators together: 1 x 12 = 12. This becomes the denominator of our answer.
-
Simplify the Fraction: Our initial result is 6/12. To simplify, we find the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 6 and 12 is 6. Divide both the numerator and the denominator by the GCD: 6 ÷ 6 = 1 and 12 ÷ 6 = 2.
-
Final Answer: Therefore, 2 x 3/12 simplifies to 1/2 or 0.5.
Beyond the Calculation: Understanding the Concept
The calculation above is straightforward, but understanding the meaning behind the process is crucial for applying fraction multiplication effectively. When we multiply 2 x 3/12, we're essentially finding two groups of three-twelfths. Imagine you have a pizza cut into 12 slices. 3/12 represents 3 slices. Multiplying by 2 means taking two sets of these 3 slices, resulting in a total of 6 slices (6/12), which simplifies to half the pizza (1/2).
Different Approaches to Solving Fraction Multiplication
While the method above is the most common, there are other ways to approach this problem:
-
Simplifying Before Multiplying: Notice that we could have simplified the fraction 3/12 before multiplying. 3/12 simplifies to 1/4. Therefore, the problem becomes 2 x 1/4 = 2/4, which also simplifies to 1/2. This approach can often make the calculation simpler, especially with larger fractions.
-
Using Decimal Equivalents: We could convert the fraction 3/12 to its decimal equivalent (0.25) and then multiply: 2 x 0.25 = 0.5, which is equivalent to 1/2. However, this approach may lead to rounding errors in more complex problems and isn't always the most efficient method.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just a classroom exercise; it's a fundamental tool used across many fields:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Multiplying fractions is essential for scaling recipes up or down. For instance, if a recipe calls for 1/2 cup of flour and you want to double the recipe, you'd multiply 1/2 x 2 to get 1 cup.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Calculations frequently involve fractions and fraction multiplication to determine the correct dimensions and quantities of materials.
-
Finance: Interest calculations, determining portions of investments, and calculating discounts all involve fraction multiplication.
-
Science: Many scientific formulas and measurements utilize fractions, making fraction multiplication essential for accurate calculations and data analysis.
-
Data Analysis: Representing data as fractions and performing calculations on them is common in data analysis, particularly when dealing with proportions and percentages.
Extending the Concept: Multiplying More Than Two Fractions
The principles discussed above extend to multiplying more than two fractions. To multiply multiple fractions, follow these steps:
- Multiply the numerators together.
- Multiply the denominators together.
- Simplify the resulting fraction.
For example: (1/2) x (2/3) x (3/4) = (1 x 2 x 3) / (2 x 3 x 4) = 6/24, which simplifies to 1/4.
Frequently Asked Questions (FAQ)
-
Q: What if the fraction is an improper fraction (numerator larger than denominator)? A: The same principles apply. Multiply the numerators and denominators, and then simplify the resulting fraction, which might still be an improper fraction. You can also convert it to a mixed number if needed (a whole number and a proper fraction).
-
Q: How do I deal with mixed numbers in multiplication? A: Convert mixed numbers into improper fractions before multiplying. For example, 1 1/2 becomes 3/2.
-
Q: Why is simplifying the fraction important? A: Simplifying ensures the answer is in its most concise and easily understandable form. It also helps avoid unnecessary complexity in further calculations.
-
Q: What if one of the numbers is a decimal instead of a fraction? A: Convert the decimal to a fraction before multiplying. For example, 0.5 is equivalent to 1/2.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a cornerstone of mathematical proficiency. While the process might seem daunting at first, breaking it down into manageable steps and understanding the underlying concepts reveals its simplicity and wide-ranging applications. From calculating baking ingredients to tackling complex engineering problems, the ability to confidently multiply fractions is a valuable skill applicable across numerous disciplines. By consistently practicing and applying these principles, you'll build a solid foundation for tackling more advanced mathematical concepts. Remember, the key is not just to get the right answer but to deeply understand the why behind each step of the process. This will empower you to confidently approach and solve even more challenging mathematical problems in the future.
Latest Posts
Latest Posts
-
98f To C
Sep 15, 2025
-
40 Times 8
Sep 15, 2025
-
6 5 Inches Cm
Sep 15, 2025
-
640km In Miles
Sep 15, 2025
-
85 4kg In Stone
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 2 X 3/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.