2 X 1/8
interactiveleap
Sep 22, 2025 · 5 min read
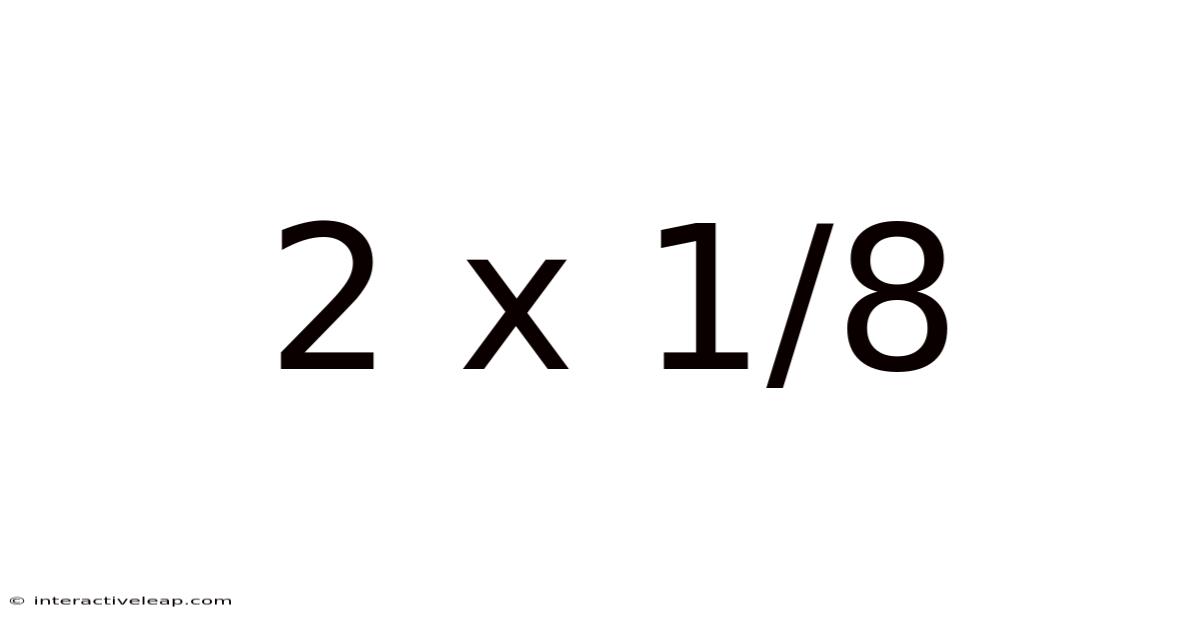
Table of Contents
Decoding 2 x 1/8: A Deep Dive into Fractions and Multiplication
Understanding fractions can seem daunting at first, but mastering them unlocks a world of mathematical possibilities. This article delves into the seemingly simple calculation of 2 x 1/8, exploring not only the solution but also the underlying principles of fraction multiplication and its broader applications. We'll cover various methods for solving this problem, explain the underlying mathematical concepts, and address common questions and misconceptions. By the end, you'll not only know the answer to 2 x 1/8 but also possess a solid understanding of fraction multiplication.
Introduction: What Does 2 x 1/8 Mean?
The expression "2 x 1/8" signifies multiplying the whole number 2 by the fraction 1/8. This might represent various real-world scenarios, such as dividing two pizzas into eighths and taking one slice from each, or calculating the total length of two pieces of ribbon, each measuring one-eighth of a meter. Understanding how to solve this problem involves understanding the fundamental principles of fraction multiplication.
Method 1: Visual Representation
A visual approach can be highly effective for understanding fraction multiplication, especially for beginners. Imagine a rectangular pizza cut into eight equal slices. 1/8 represents one of these slices. 2 x 1/8 means taking two of these slices. Visually, you can see that this represents 2/8 of the whole pizza.
This visual method is particularly helpful in grasping the concept of multiplying a fraction by a whole number. It directly translates the abstract mathematical operation into a concrete, easily understandable representation.
Method 2: Converting to an Improper Fraction
Another approach involves converting the whole number into a fraction. The whole number 2 can be expressed as 2/1. Now the problem becomes:
(2/1) x (1/8)
To multiply fractions, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(2 x 1) / (1 x 8) = 2/8
This method uses a more formal mathematical approach, which is essential for tackling more complex fraction multiplications. The result, 2/8, is equivalent to the result obtained through the visual method.
Method 3: Simplifying Fractions
The fraction 2/8 is not in its simplest form. To simplify, we find the greatest common divisor (GCD) of both the numerator and denominator. In this case, the GCD of 2 and 8 is 2. We divide both the numerator and the denominator by the GCD:
2/8 ÷ 2/2 = 1/4
Therefore, 2 x 1/8 simplifies to 1/4. This simplified fraction represents the most concise and efficient way to express the answer. Simplifying fractions is crucial for ensuring clarity and ease of understanding in subsequent calculations.
Method 4: Understanding the Concept of Multiplication
At its core, multiplication represents repeated addition. 2 x 1/8 means adding 1/8 to itself two times:
1/8 + 1/8 = 2/8 = 1/4
This reinforces the understanding that multiplication is a shortcut for repeated addition. This approach is particularly useful for understanding the fundamental concept of multiplication applied to fractions. While it might be less efficient for complex calculations, it provides a strong conceptual foundation.
The Mathematical Principles Behind Fraction Multiplication
The process of multiplying fractions involves several fundamental mathematical concepts:
-
Numerators and Denominators: Fractions consist of two parts: the numerator (top number) and the denominator (bottom number). The denominator represents the total number of equal parts, while the numerator represents the number of parts being considered.
-
Multiplying Numerators and Denominators: When multiplying fractions, we multiply the numerators together and the denominators together separately. This is a fundamental rule of fraction arithmetic.
-
Simplifying Fractions (Reducing to Lowest Terms): Simplifying a fraction involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD to obtain an equivalent fraction in its simplest form. This ensures the fraction is represented in its most concise and easily understood form.
-
Equivalent Fractions: Different fractions can represent the same value. For example, 2/8 and 1/4 are equivalent fractions, both representing one-quarter. Understanding equivalent fractions is crucial for simplifying and comparing fractions.
-
Whole Numbers as Fractions: Any whole number can be expressed as a fraction with a denominator of 1. This allows us to apply the rules of fraction multiplication consistently to calculations involving both whole numbers and fractions.
Real-World Applications of Fraction Multiplication
The ability to multiply fractions is essential in numerous real-world situations:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Multiplying fractions is necessary when scaling a recipe up or down.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Calculations often involve multiplying fractions to determine accurate dimensions and quantities.
-
Finance: Calculating interest, discounts, and proportions often involves fraction multiplication.
-
Data Analysis: Many data analysis tasks involve calculating proportions and percentages, which require a strong understanding of fraction multiplication.
Frequently Asked Questions (FAQ)
-
Q: Why do we multiply the numerators and denominators separately?
A: This is a fundamental rule of fraction arithmetic derived from the concept of representing fractions as areas or parts of a whole. Multiplying numerators and denominators separately reflects the combined effect of these parts.
-
Q: What if I have more than two fractions to multiply?
A: The same principle applies. Multiply all the numerators together and all the denominators together, then simplify the resulting fraction.
-
Q: What if one of the numbers is a mixed number (e.g., 1 1/2)?
A: Convert the mixed number into an improper fraction first (e.g., 1 1/2 becomes 3/2) and then proceed with the multiplication.
-
Q: Is there a way to check my answer?
A: You can use visual representations, estimation, or try working backwards from the simplified answer to verify your calculation.
Conclusion: Mastering Fractions – A Building Block for Success
Mastering fraction multiplication, as exemplified by solving 2 x 1/8, is a crucial step in developing a strong foundation in mathematics. This seemingly simple problem encapsulates fundamental mathematical principles with far-reaching applications in various fields. By understanding the methods, the underlying concepts, and the real-world relevance, you gain more than just the answer; you gain a deeper appreciation for the power and versatility of mathematics. Remember, consistent practice and a clear understanding of the underlying concepts are key to mastering fractions and achieving mathematical success. Don't be afraid to experiment with different methods and find the approach that works best for you. The journey of learning mathematics is a continuous process of exploration and discovery.
Latest Posts
Latest Posts
-
Heavy Duty Screwdriver
Sep 22, 2025
-
150grams To Oz
Sep 22, 2025
-
Water Soluble Oils
Sep 22, 2025
-
Electrolysis Half Equations
Sep 22, 2025
-
Column Method Subtraction
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 X 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.