2/5 Of 45
interactiveleap
Sep 15, 2025 · 6 min read
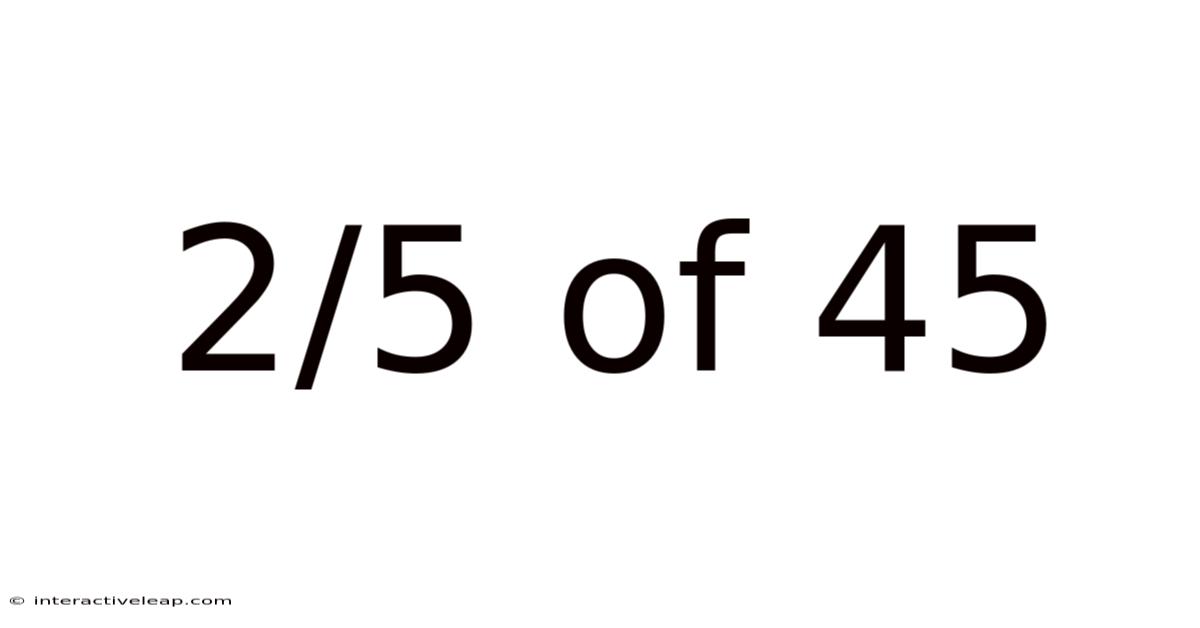
Table of Contents
Decoding 2/5 of 45: A Comprehensive Guide to Fractions and Multiplication
Understanding fractions and how to apply them in real-world scenarios is a fundamental skill in mathematics. This article delves into the seemingly simple problem of calculating "2/5 of 45," providing not just the answer but a comprehensive understanding of the underlying concepts and their practical applications. We will explore various methods for solving this problem, address common misconceptions, and delve into the broader context of fraction multiplication and its relevance in everyday life. This guide is designed for learners of all levels, from those just beginning to grasp the basics of fractions to those seeking a deeper understanding of mathematical principles.
Understanding the Problem: 2/5 of 45
The phrase "2/5 of 45" essentially translates to a multiplication problem involving fractions. The word "of" in this context indicates multiplication. Therefore, we are tasked with finding the product of 2/5 and 45. This seemingly simple problem allows us to explore several different approaches to solving fraction multiplication, reinforcing our understanding of core mathematical concepts.
Method 1: Converting the Whole Number to a Fraction
One straightforward method is to convert the whole number 45 into a fraction. Any whole number can be expressed as a fraction by placing it over 1. In this case, 45 becomes 45/1. Now, our problem becomes:
(2/5) * (45/1)
To multiply fractions, we simply multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(2 * 45) / (5 * 1) = 90/5
Finally, we simplify the resulting fraction by dividing the numerator by the denominator:
90/5 = 18
Therefore, 2/5 of 45 is 18.
Method 2: Simplifying Before Multiplication
A more efficient approach involves simplifying the fractions before multiplying. Notice that 45 and 5 share a common factor: 5. We can simplify the problem by dividing both 45 (in the numerator of 45/1) and 5 (in the denominator of 2/5) by their greatest common divisor, which is 5:
(2/5) * (45/1) = (2/1) * (9/1) = 18
This method reduces the size of the numbers we are working with, making the calculation easier and less prone to errors. This highlights the importance of simplifying fractions whenever possible to streamline the calculation process.
Method 3: Understanding the Concept of "Of"
The word "of" in mathematics often signifies multiplication, particularly when dealing with fractions and percentages. Let's break down what "2/5 of 45" means conceptually. We are essentially dividing 45 into 5 equal parts and then taking 2 of those parts.
- Divide: 45 / 5 = 9 (Each of the five equal parts is 9).
- Multiply: 9 * 2 = 18 (Taking two of those parts gives us 18).
This method provides a clear visual representation of the problem, making it easier to grasp the underlying concept, especially for visual learners. This approach is particularly helpful for understanding the practical application of fractions in real-world situations.
Method 4: Using Decimal Equivalents
We can also solve this problem by converting the fraction 2/5 into its decimal equivalent. Dividing 2 by 5 gives us 0.4. The problem now becomes:
0.4 * 45
Multiplying 0.4 by 45 results in 18.
This approach highlights the interchangeability between fractions and decimals, demonstrating another method to arrive at the correct answer. This is a useful technique when working with calculators or when dealing with problems that involve both fractions and decimals.
Expanding the Understanding: Fractions and Their Applications
The problem "2/5 of 45" serves as a gateway to understanding a broader range of mathematical concepts related to fractions. Let's explore some of these concepts:
- Numerator and Denominator: The top number of a fraction (e.g., 2 in 2/5) is called the numerator, representing the number of parts we are considering. The bottom number (e.g., 5 in 2/5) is called the denominator, representing the total number of equal parts.
- Simplifying Fractions: Reducing a fraction to its simplest form involves dividing both the numerator and the denominator by their greatest common divisor. This simplifies calculations and makes the fraction easier to understand.
- Fraction Multiplication: Multiplying fractions involves multiplying the numerators together and the denominators together.
- Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 1 1/2). These can be converted into improper fractions (where the numerator is larger than the denominator) for easier calculations.
- Equivalent Fractions: Different fractions can represent the same value (e.g., 1/2 = 2/4 = 3/6). Understanding equivalent fractions is crucial for simplifying and comparing fractions.
Real-World Applications of Fractions
Fractions are not just abstract mathematical concepts; they are essential tools used in various aspects of daily life:
- Cooking and Baking: Recipes often use fractions to specify ingredient quantities (e.g., 1/2 cup of sugar, 2/3 cup of flour).
- Measurement: Measuring length, weight, and volume frequently involves fractions (e.g., 1/4 inch, 1/2 pound, 1/3 liter).
- Finance: Understanding fractions is essential for dealing with percentages, interest rates, and proportions in financial calculations.
- Construction and Engineering: Fractions play a vital role in blueprints, design specifications, and precise measurements in construction and engineering projects.
Common Misconceptions about Fractions
Several common misconceptions can hinder the understanding and application of fractions:
- Confusion with Decimal Addition/Subtraction vs. Multiplication: Students sometimes incorrectly apply the rules of addition or subtraction to multiplication of fractions. Remember, multiplying fractions involves multiplying numerators and denominators separately.
- Difficulty Simplifying Fractions: Many students struggle with finding the greatest common divisor to simplify fractions effectively. Practice and familiarity with divisibility rules can help overcome this difficulty.
- Misinterpreting "Of": The word "of" is often misinterpreted in fraction problems, leading to incorrect calculations. Remembering that "of" signifies multiplication is crucial.
Frequently Asked Questions (FAQ)
Q: Can I solve this problem using a calculator?
A: Yes, you can. Most calculators can handle fraction multiplication. However, understanding the underlying concepts is crucial for applying fractions in various contexts even without a calculator.
Q: What if the fraction was a larger number, such as 17/25 of 45?
A: The same principles apply. You would multiply 17/25 by 45/1, simplify if possible, and then solve.
Q: Are there other ways to represent the answer?
A: Yes, the answer 18 can be represented as 18/1, or as a percentage (100%).
Q: What if the question asked for a different fraction of 45?
A: The same methods would apply. You would simply replace 2/5 with the given fraction and follow the same steps.
Conclusion: Mastering Fractions – A Building Block for Mathematical Success
The seemingly simple problem of calculating "2/5 of 45" opens up a world of possibilities in understanding fractions and their applications. By exploring different methods and addressing common misconceptions, we've gained a deeper appreciation for the fundamental principles underlying fraction multiplication. Mastering these concepts is not just about solving individual problems; it's about building a strong foundation in mathematics that will be valuable in various aspects of life, from everyday tasks to complex calculations. Remember to practice regularly, explore different approaches, and don't hesitate to seek clarification when facing challenges. The journey to mathematical proficiency is a continuous process of learning and refinement. Through consistent effort and a willingness to understand the underlying principles, you can confidently tackle any fraction problem that comes your way.
Latest Posts
Latest Posts
-
800 Grams Ounces
Sep 15, 2025
-
95 3kg In Stone
Sep 15, 2025
-
30 Of 110
Sep 15, 2025
-
66 6 To Fraction
Sep 15, 2025
-
Box With X
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 2/5 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.